適用于風電場的最佳電池容量選取的方法

楊水麗，惠 東，李建林，梁 亮，李 蓓

（中國電力科學研究院，北京市，100192）

0 引言

風力發電技術日趨成熟，風電場的建設也在逐步加快。但是，由于風電輸出受天氣和地理條件等影響具有很大的波動特性，導致風電輸出對電力系統的安全性與穩定性會造成很大的影響，這在一定程度上制約了風電的快速發展。因此，為了促進風能的利用與發展，必須減小風電的輸出波動。

本文致力于風電輸出波動的平滑技術研究，依據成本/性能比，利用計算機仿真來推導獲取最佳電池功率與容量。

目前，日本和芬蘭等國家對風電功率波動的平滑化進行了比較深入的研究，并提出了應用儲能平滑風電波動的運算法則及評估標準[1-2]。在對風電輸出波動平滑效果的判據方面，日本的研究者提出了平滑時間常數-電池容量特性和平滑時間常數-系統輸出效率特性[2]，依據成本/性能比得出最佳的電池容量。而平滑時間常數-系統輸出效率特性的獲取依賴于實際應用的儲能系統的效率，在儲能系統的電池類型未確定的情況下，則存在獲取儲能系統效率困難的問題，故此判據存在一定的局限性。

在研究平滑時間常數-電池容量特性的基礎上，本文提出了一種新的判據，即平滑時間常數-合成輸出標準偏差特性。通過分析這2種特性之間的特點，同時依據成本/性能比來確定合適的時間常數，使其既能滿足風電輸出平滑化的需求，又能使電池容量比較小，而且在儲能系統的儲能電池未確定的情況下，也能得出最佳的儲能系統參數。

1 平滑化原理及評估指標

利用電池存儲系統來平滑風電輸出的波動，通過控制電池存儲系統使風電功率輸出和電池存儲系統功率輸出的總和嚴格追隨著輸出目標值。輸出目標值的大小通過1個低通濾波器過濾風電輸出功率而得到。電池出力要求值為輸出目標值與風電出力的差，如果電池輸出是正值，表示電池放電；如果電池輸出是負值，則表示電池充電。最后，系統輸出（合成輸出）是電池輸出與風電輸出的總和。所需存儲系統功率與容量的求取在文獻[1]中有詳細描述。

對風電輸出波動平滑的效果分析采用2個評估指標，即風電輸出的標準偏差和波動變化率。

（1）標準偏差。

標準偏差可以衡量一個隨機變量偏離它的均值程度。若曲線越平滑，標準偏差越小，表征隨機變量偏離均值越小。在這里用標準偏差作為評估長時間段內風電輸出波動的評估指標。

（2）輸出波動的變化率。

波動的變化率為相鄰兩輸出差的絕對值，這是一個評估短時間段內風電輸出波動的評估指標。

2 實例計算

實例計算依據張北某風電場49.5 MW級系統的能源管理系統（energy management system，EMS）中10個月（2008年6月—2009年3月）的功率數據，采集時間間隔為5 min，風電功率所測數據如圖1所示。

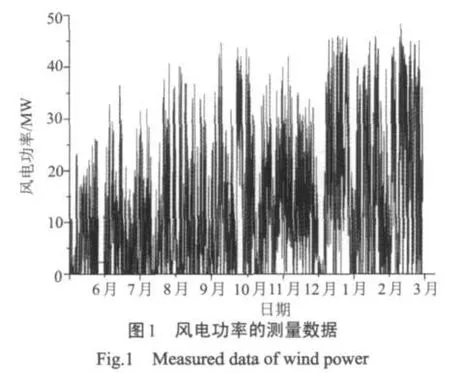
由圖1可知，其風電出力特性為：全網風電低于10%額定功率的概率為38%，出力為20%～30%額定功率的概率為14%，而出力超過50%額定功率的概率為15%。對風電出力特性的研究，有益于最佳電池容量選取的經濟性分析。

風電功率波動的變化率如圖2所示。由圖2可知，風電功率波動變化率分布在20%額定功率值（10 MW）范圍內，其最大的波動變化率達到40%額定功率值（20 MW）。由此可見，未加入儲能系統的風電功率的波動是大而頻繁的，因此需要加入儲能系統對其波動進行平滑。

依據此風電系統功率測量數據，以不同時間常數t來計算輸出目標值，功率積分區間為1天，得出平滑所需的電池功率與電池容量，然后統計電池功率與電池容量的主要概率分布區域，得出最佳的儲能系統的功率與容量大小。計算結果如表1所示，不同平滑時間常數下對應的平滑效果如圖3所示。

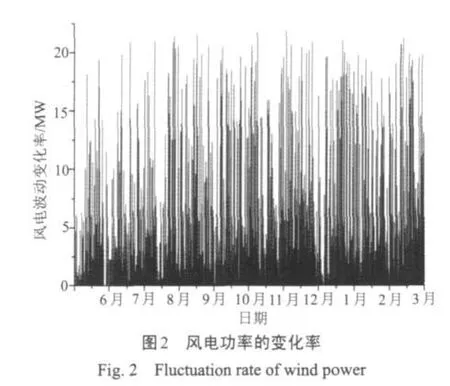
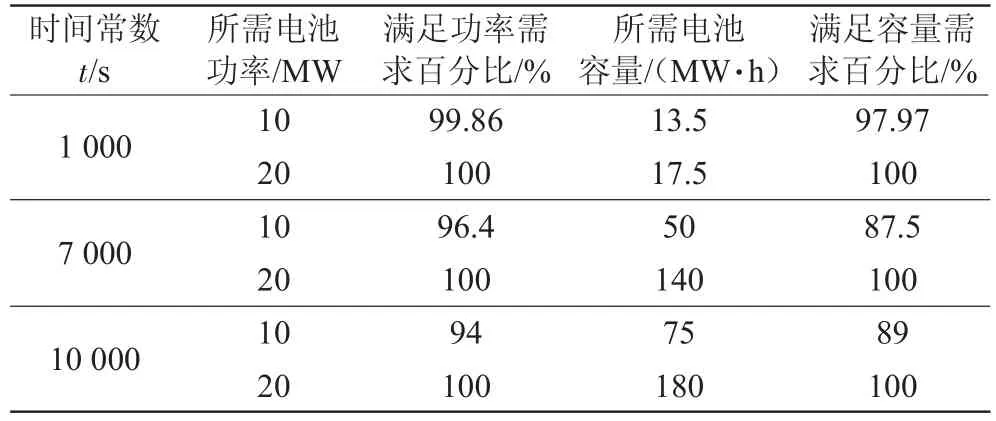
表1 不同平滑時間常數下所需電池功率與容量Tabb.1 Battery power and capacity needed under different time constants

由表1和圖3可知，隨著平滑時間常數的增大，平滑效果越好，但所需電池功率和電池容量也隨之增大。因此，從性能與成本的角度來考慮，需要選取一個既能達到較好的平滑效果，又能比較經濟的平滑時間常數。

3 平滑時間常數-合成輸出標準偏差特性

由于所需電池功率與容量的求取是以功率積分區間為1天，統計303天（10個月）的電池功率與容量的主要概率分布區域來得出最佳值。因此，則可選取特征日（2008年6月1日）的輸出數據來對平滑時間常數-電池容量特性和平滑時間常數-合成輸出標準偏差特性進行分析，得出最佳的平滑時間常數。

平滑時間常數與電池容量成正比關系，如圖4所示（2008年6月1日）。而標準偏差與平滑效果呈相對的反比關系，因此，可得出時間常數-合成輸出標準偏差的特性關系，如圖5所示（2008年6月1日）。

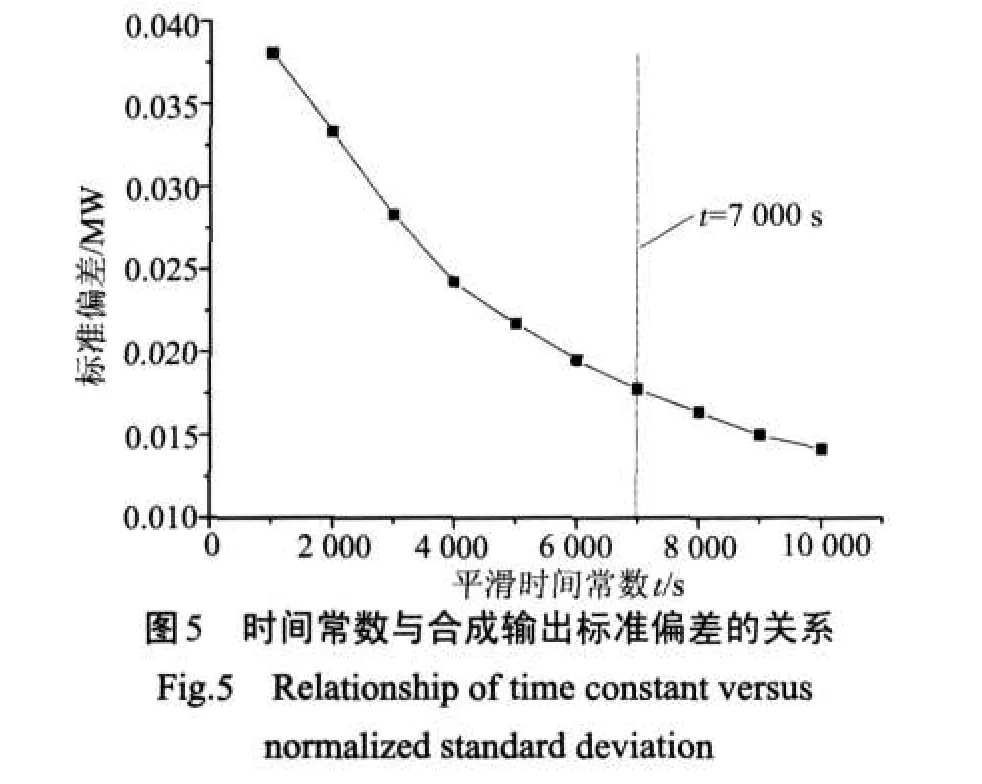
由圖5可知，合成輸出的標準偏差隨時間常數的增加而減小，當時間常數增大，合成輸出的標準偏差減小，即表示電池容量越大，合成輸出偏離它均值的偏差越小，得到的合成輸出曲線越平滑。但當平滑時間常數增大到7000 s的時候，隨著平滑時間常數的增大，標準偏差減小的幅度緩慢，對合成輸出曲線平滑效果的改善越來越不顯著。

由圖3也可以非常直觀地看出，隨著時間常數t的增大，合成出力的曲線愈平滑，但平滑的效果隨著t的增大越發地趨于接近，當時間常數超過7000 s后，對平滑效果的改善越來越小。

選擇中節能風電場其他日的功率數據進行平滑時間常數-電池容量特性和平滑時間常數-合成輸出標準偏差特性分析，仍發現當時間常數超過7000 s后，所需電池容量增大，但對平滑效果的改善越來越不顯著。

因此，從成本/性能的視角來說，7000 s是適用于本風電場的最佳平滑時間常數。對應此平滑時間常數的電池功率選取10 MW，電池容量選取50 MW·h，是假定系統設置最佳的參數，如表2所示。

表2 最佳平滑時間常數對應的所需電池功率與容量Tab.2 Battery power and capacity underr optimal time constants

由于風電場風資源的不同，平滑時間常數7000 s不一定是任意50 MW級風電系統的最經濟參數，但此判據與推導方法適用于任意功率等級任意風電場儲能系統參數的選定。

4 平滑結果分析

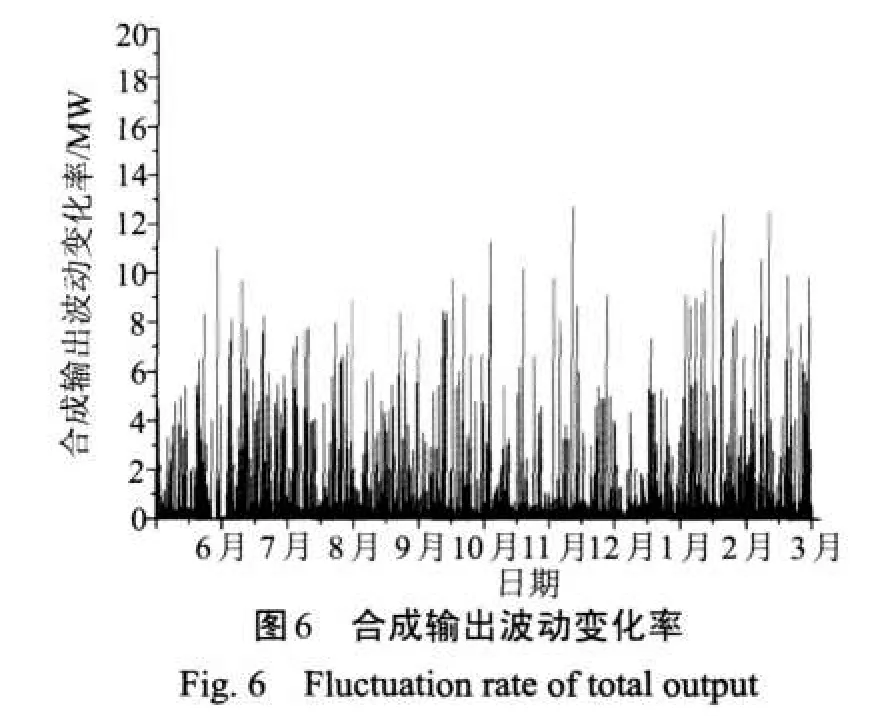
選取平滑時間常數7000 s、電池功率10 MW以及電池容量50 MW·h對風電輸出進行平滑時，平滑效果通過比較圖2和圖6（t=7000 s）的功率波動變化率來檢驗。

（1）由圖2可知，風電原始輸出的功率波動變化率主要分布在20%額定功率值（10 MW）范圍內，功率波動變化率分布在2%額定功率值（1 MW）范圍內的比例為96%；

（2）當選取平滑時間常數t為7000 s進行平滑后，合成輸出功率波動的變化率主要集中在4%額定功率值（2 MW）范圍內，功率波動變化率分布在2%額定功率值范圍內的比例為99.5%，如圖6所示。

通過比較得知，對風電出力進行平滑后，功率波動的變化率得到了有效的壓制，功率波動的變化率的主要分布區域由20%減小到了4%額定功率值范圍內。因此，對功率波動的平滑是成功的。

5 結論

本文通過電池功率、電池容量與平滑效果的定量關系，得出平滑時間常數-電池容量特性與平滑時間常數-合成輸出標準偏差特性，依據成本/性能比得到應用于風力發電系統的存儲系統最優化的設計。此推導方法適用于不同等級的任意風電場的儲能系統參數的選定。

[1]Jukka V P，Peter D L.Effect of energy storage on variations in wind power[J].Wind Energy，2005，8（4）：424-441.

[2]Shiji W，Ryohei O.An investigation on optimal battery capacity in wind power generation system[R].Dept.of EE&Bioscience，Waseda University，Tokyo，Japan.

[3]Key T，GomatomK，Kamath H.Smoothing short-term power fluctuations[R].California,EPRI，2005.

[4]Jantharamin N，Zhang L.A new dynamic model for Lead-Acid batteries[J].Institute of Electrical Engineering CAS，IEEE Xplore，2009：86-90.

[5]Zbigniwe L，Janusz W B.Supervisory control of a wind farm[J].IEEE Transactions on Power Systems，2007，22（3）：985-994.

[6]Mary B，Goran S.Value of bulk energy storage for managing wind power fluctuations[J].IEEE Transactions on Energy Conversion，2007，22（1）：197-205.

[7]Iulian M，Seddik B，Antoneta Iuliana，Energy-Reliability optimization of wind energy conversion systems by sliding mode control[J].IEEE Transactions on Energy Conversion，2008，23（3）：975-985.

[8]Johan H E.Interconnecting large-scale wind power to transmission networks[C].IEEE PES Power Africa 2007 Conference and Exposition Johannesburg，SouthAfrica，2007.

[9]Masashi A，Akihiko Y，Yasuyuki T.Evaluation of battery system for frequency control in interconnected power system with a large penetration of wind power generation[C].International Conference on PowerSystem Technology，North ChinaElectricPower Vniversity，2006：1-7.

[10]Vladislav A，Peter B E.A large wind power system in almost island operation-a Danish case study[J].IEEE，2007，22（3）：937-943.

[11]Chen Z.Issues of connecting wind farms into power systems[C].IEEE/PES Transmission and Distribution Conference&Exhibition∶Asia and Pacific，Dalian，2005.

[12]張步涵，曾 杰，毛承雄，等.電池儲能系統在改善并網風電場電能質量和穩定性中的應用[J].電網技術，2006，30（14）：54-58.

[13]李春蘭，晁 勤.風電系統電磁暫態數學模型及其仿真[J].計算機仿真，2006，23（4）：220-224.

[14]徐家澎.風力發電場接入系統方案分析[J].內蒙古電力技術，1999，17（6）：6-14.

[15]張紅光，張粒子，陳樹勇，等.大容量風電場接入電網的暫態穩定特性和調度對策研究[J].中國電機工程學報，2007，27（31）：45-51.

[16]吳義純，丁 明，張立軍.含風電場的電力系統潮流計算[J].中國電機工程學報，2005，25（4）：36-39.

[17]李 蓓，郭劍波，惠 東，等.液流儲能電池在電網運行中的效率分析[J].中國電機工程學報，2009，29（35）：1-6.