水輪發(fā)電機組單機軸系統(tǒng)扭轉(zhuǎn)振動特性研究
賈 山,劉 彬
(1.通河縣水務局,黑龍江通河 150900;2.通河縣水利勘測設計隊,黑龍江通河 150900)
由于轉(zhuǎn)輪水力轉(zhuǎn)矩不均勻、外部負荷不穩(wěn)定、電氣事故等原因,造成機組電力系統(tǒng)振蕩和軸系扭轉(zhuǎn)振動。此時機組轉(zhuǎn)速、電流、電壓、功率、轉(zhuǎn)矩等都將發(fā)生周期性變動或振蕩,其幅值可達到較大的數(shù)值。因此,振蕩對機組以及與其相聯(lián)的有關(guān)設備都是不利的,甚至造成電機失步。
目前計算機組軸系統(tǒng)扭轉(zhuǎn)自振頻率的方法是將機組軸系統(tǒng)和定子均簡化成剛體,振蕩時將轉(zhuǎn)子和定子之間的電磁轉(zhuǎn)矩變化處理成一個等效機械彈簧,屬于單自由度的扭轉(zhuǎn)問題[1]。這種簡化方法,對于轉(zhuǎn)子支臂具有較大切向剛度的機組來說,是能滿足精度要求的,如整體鑄造的轉(zhuǎn)子機架,與磁軛圈合為一體的轉(zhuǎn)子支架,或圓盤式轉(zhuǎn)子機架。上述轉(zhuǎn)子機架的切向剛度大,支臂的彈性耦合作用對電機的扭轉(zhuǎn)自振頻率影響不大。但是組合式轉(zhuǎn)子機架的切向剛度較小,電機振蕩時支臂的彈性作用參與耦合振動,使機組軸系統(tǒng)的扭轉(zhuǎn)自振頻率降低,因此,采用有限元法并考慮軸系和各構(gòu)件的彈性作用,可能更準確合理。
1 基本假設和計算條件
當機組軸系統(tǒng)發(fā)生扭轉(zhuǎn)振動時,將有一個交變的電磁力矩作用在發(fā)電機定子上。此時定子和上機架對扭轉(zhuǎn)振動會不會產(chǎn)生耦合作用,值得關(guān)注[2]。計算表明,由于定子的扭轉(zhuǎn)剛度較大,對軸系統(tǒng)的扭轉(zhuǎn)自振頻率幾乎不發(fā)生耦合作用。因此,可以將定子簡化為剛體,轉(zhuǎn)動部件處理成具有集中質(zhì)量的彈性連續(xù)梁,并通過轉(zhuǎn)子磁軛處的交變電磁力與定子相連。推力瓦與鏡板的摩擦,對軸系統(tǒng)扭轉(zhuǎn)自振頻率影響很小,可以忽略推力軸承的作用,計算模型如圖1(a)。軸系統(tǒng)繞大軸軸線Y扭振,J1、J2分別為勵磁機和轉(zhuǎn)子支臂中心體的轉(zhuǎn)動慣量;J3為水輪機轉(zhuǎn)輪及其水體附加質(zhì)量的轉(zhuǎn)動慣量;M為磁軛和磁極質(zhì)量。轉(zhuǎn)子支臂簡化成無重梁,只考慮其剛度,將質(zhì)量按適當比例分配給支臂中心體和勵磁機及磁極。在圖1(b)中θ為大軸扭轉(zhuǎn)角,逆時針方向為正;u為轉(zhuǎn)子磁軛切向位移,以轉(zhuǎn)子支臂內(nèi)端為零參考點。
2 有限元矩陣分析的公式推導
2.1 大軸平衡方程
將大軸分成n個結(jié)點。設轉(zhuǎn)子有S條支臂,扭振時每條支臂對大軸b點(見圖2(a))的作用力矩為S(R1Q+M1)。
矩陣有限元法的單元剛度矩陣為:


圖1 機組軸系統(tǒng)扭轉(zhuǎn)振動計算簡圖

圖2 發(fā)電機轉(zhuǎn)子計算簡圖
單元質(zhì)量陣為:
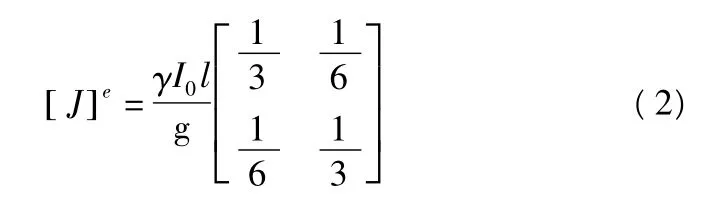
單元位移分量為:

式中:G為剪切模量,I0為極慣性矩;GI0為扭轉(zhuǎn)剛度;γ為容重;l為單元長度;g為重力加速度;為單元轉(zhuǎn)動慣量。
單元力的平衡方程為:
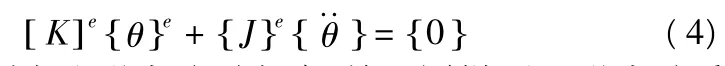
采用直接剛度法形成總剛度陣,并以同樣原理形成總質(zhì)量陣后,再考慮結(jié)點處荷載,得大軸整體力的平衡方程組如下:

2.2 發(fā)電機轉(zhuǎn)子力的平衡方程
如前所述,轉(zhuǎn)子支臂重量遠小于磁軛重量,只考慮其剛度,而將其質(zhì)量按適當比例分配給支臂兩端。圖2(b)中M為磁軛分配給每條支臂的集中質(zhì)量。扭轉(zhuǎn)運動的脫離體見圖2(c),圖中K1為支臂平移剛度;K2為電磁力矩變化值轉(zhuǎn)換成相應支臂的等效機械平移剛度。由圖2(c)推出隔離體磁軛力的平衡方程為:

式中:V=R2θb+U是質(zhì)量M的絕對位移。將V=R2θb+U代入式(4-2)后,得:

對支臂隔離體分別列出力及力矩的平衡方程:

支臂可看成是兩端固定梁,A為待定系數(shù),其值可根據(jù)磁軛端支臂相對轉(zhuǎn)角為零的邊界條件求出。將上式寫成:

將公式(9)代入公式(5)后,得:


將式(11)和(8)式擴陣后形成總體平衡方程組:

3 算例分析
3.1 計算基本數(shù)據(jù)
計算中取大軸材料的剪切模量為8.1×104N/mm2,容重為0.000078 N/mm3;轉(zhuǎn)子中心體的轉(zhuǎn)動慣量為6.05×1012N·mm2,水輪機轉(zhuǎn)輪及其水體附加質(zhì)量的轉(zhuǎn)動慣量為2.72×1012N·mm2,轉(zhuǎn)子支臂剛度1.0×1010N/mm。上述數(shù)值系根據(jù)有關(guān)設計手冊和經(jīng)驗選取。
3.2 軸系扭轉(zhuǎn)自由振動特性計算結(jié)果及分析
對軸系頻率和振型的決定性影響因素可能是導軸承和推力軸承的扭轉(zhuǎn)動力剛度系數(shù),以及定子和轉(zhuǎn)子間的磁場作用。計算中,考慮轉(zhuǎn)子支臂的質(zhì)量,定子和轉(zhuǎn)子間的磁場強度,各主要部件的集中轉(zhuǎn)動慣量,以及水體的耦聯(lián)作用[3]。表1為軸系的扭轉(zhuǎn)自振頻率,圖3分別給出了扭轉(zhuǎn)振動的前四階振型。

表1 前四階自振頻率

圖3 軸系扭轉(zhuǎn)振動的前四階振型
3.3 扭振特性的敏感性分析
計算分析方法同上。逐一分析各個影響因素對扭轉(zhuǎn)自振頻率的作用,包括:轉(zhuǎn)子轉(zhuǎn)動慣量、水體對轉(zhuǎn)輪附加轉(zhuǎn)動慣量、轉(zhuǎn)子支臂剛度。
3.3.1 轉(zhuǎn)子轉(zhuǎn)動慣量AI1(N·mm2)的影響
圖4(a)、(b)、(c)、(d)為各階頻率隨轉(zhuǎn)子轉(zhuǎn)動慣量變化的曲線圖。自振頻率f(Hz)隨著轉(zhuǎn)子轉(zhuǎn)動慣量AI1(N·mm2)的增大而減小,前兩階頻率變化較為明顯。第一階頻率的變化趨于線性,而第二、三、四階頻率的變化呈曲線型。這里所取的變化范圍較大,是為了說明其影響,可以看出對前兩階頻率的影響還是十分明顯,尤其是第一階頻率更明顯。實際設計中在一定范圍內(nèi)改變轉(zhuǎn)動慣量從而改變扭振特性也是可行的。

圖4 扭轉(zhuǎn)自振頻率與轉(zhuǎn)子轉(zhuǎn)動慣量的關(guān)系曲線
3.3.2 轉(zhuǎn)輪水體附加轉(zhuǎn)動慣量AI2(N·mm2)的影響
自振頻率f(Hz)隨著水體附加轉(zhuǎn)動慣量AI2(N·mm2)的增大而減小,第一階頻率變化較為明顯,圖5(a)、(b)、(c)、(d)為各階頻率隨水體對轉(zhuǎn)輪附加轉(zhuǎn)動慣量變化的曲線圖。

圖5 扭轉(zhuǎn)自振頻率與水體對轉(zhuǎn)輪附加轉(zhuǎn)動慣量的關(guān)系曲線
水體附加轉(zhuǎn)動慣量的作用對前兩階頻率十分突出,在計算中必須考慮其影響。但須注意的是,這里只是為了說明其影響程度,因為實際上我們不可能改變其數(shù)值。
3.3.3 轉(zhuǎn)子支臂剛度AMK(N/mm)的影響
自振頻率f(Hz)隨著轉(zhuǎn)子支臂剛度AMK(N/mm)的增大而增大,前兩階頻率變化較為明顯,圖6(a)、(b)、(c)、(d)為各階頻率隨轉(zhuǎn)子支臂剛度變化的曲線圖。
轉(zhuǎn)子支臂剛度的影響也主要體現(xiàn)在前兩階上,尤其是對第一階頻率,提高轉(zhuǎn)子支臂剛度對提高頻率作用顯著,主要是因為磁軛端部的質(zhì)量較大,支臂支承剛度的作用就十分重要。

圖6 扭轉(zhuǎn)自振頻率與轉(zhuǎn)子支臂剛度的關(guān)系曲線
4 結(jié)論
轉(zhuǎn)輪水力轉(zhuǎn)矩不均勻、外部負荷不穩(wěn)定、電氣事故等多種原因,將造成機組電力系統(tǒng)振蕩和軸系扭轉(zhuǎn)振動。這樣對機組以及與其相聯(lián)的有關(guān)設備都是不利的,甚至造成電機失步。本文研究了機組扭轉(zhuǎn)振動的自振特性,同時也進行了敏感性分析。計算時采用了有限元法并考慮了軸系統(tǒng)各構(gòu)件的彈性作用。
從以上的計算分析結(jié)果中可看出,轉(zhuǎn)子轉(zhuǎn)動慣量、水體對轉(zhuǎn)輪附加轉(zhuǎn)動慣量、轉(zhuǎn)子支臂剛度都是機組扭轉(zhuǎn)振動的影響因素。在實際的機組設計中,可以通過改變轉(zhuǎn)子轉(zhuǎn)動慣量和轉(zhuǎn)子支臂剛度,改變機組的扭振特性。隨著轉(zhuǎn)子轉(zhuǎn)動慣量的減小和轉(zhuǎn)子支臂剛度的升高,自振頻率會增大。雖然水體轉(zhuǎn)動慣量對機組自振頻率的影響也很大,但是這一因素我們卻無法改變。
[1]楊代立,董毓新.立軸水輪發(fā)電機組的扭振特性[J].大電機技術(shù),1984(5):1-6.
[2]г.и,克里夫琴科.水電站動力裝置中的過渡過程[M].北京:水利出版社,1980.
[3]白延年.水輪發(fā)電機設計與計算[M].北京:機械工業(yè)出版社,1982.

