基于不同分布的巖石損傷本構模型的比較
岳 洋
目前,巖石材料損傷力學研究的方法主要有:1)應用連續介質損傷力學,以內變量的方法從宏觀上處理損傷問題;2)從唯象學角度出發并根據統計分布理論,假設損傷參量服從某種分布,導出巖石損傷方程。顯然,后一種辦法所得結果更加合理。近年來,由于統計損傷理論的引入,使得巖石本構關系的研究取得了一定程度的突破。國內學者唐春安[2]、曹文貴[3-5]、徐衛亞[6]、許江[7,8]等均在這方面進行過研究,促進了巖石統計損傷力學的發展。本文基于應變強度理論,分別假定巖石微元強度服從Weibull分布和冪函數分布,建立了基于兩種分布的巖石損傷本構模型,用實測試驗資料對其進行了驗證,并對兩種模型進行了比較分析。
1 兩種損傷模型的建立
1.1 基于Weibull分布的損傷模型的建立
假定巖石微元強度服從Weibull分布,其概率密度函數為[2]:
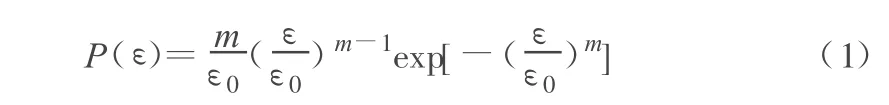
其中,P(ε)為巖石微元強度分布函數;ε為微元強度隨機分布的分布變量;m,ε0均為分布參數。
假設某一級荷載下已破壞的微元數目為n,定義統計損傷變量D為已破壞的微元體數目與總微元數目N之比。則:

其中,D為巖石損傷變量;n為某級荷載下已破壞的微元數目;N為無損巖石材料的總微元數目。
當加載到某一水平F時,破壞的微元數目為:
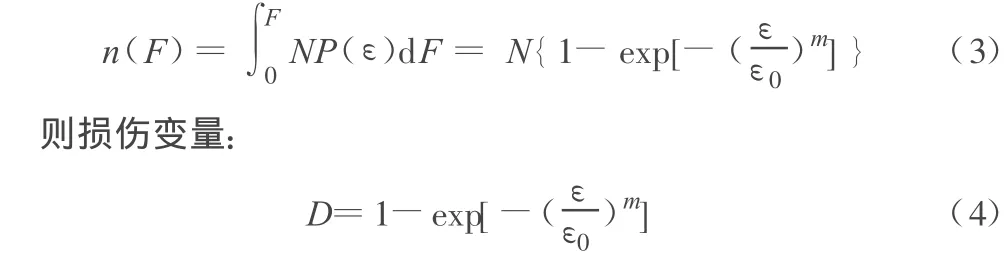
假定巖石微元破壞前服從廣義虎克定律,由連續介質損傷力學理論可得如下本構關系[2]:

其中,E,ε分別為無損巖石的彈性模量和應變量。
將式(4)代入式(5),根據廣義虎克定律,可以得到基于Weibull分布的三維應力作用下巖石損傷統計本構模型為:
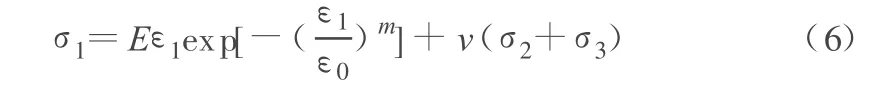
1.2 基于冪函數分布的損傷模型的建立
假定巖石微元強度服從冪函數分布,其概率密度函數為[5]:

將式(9)代入式(5),根據廣義虎克定律,可以得到基于冪函數分布的三維應力作用下巖石損傷統計本構模型為:
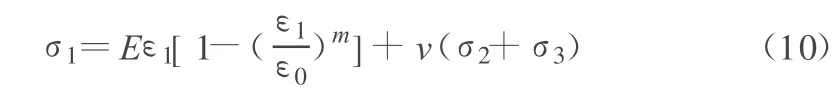
1.3 分布參數的確定
式(6)和式(10)中的分布參數m和ε0可通過將兩式兩邊取對數進行線性化處理[4]得到。式(6)和式(10)變形后可分別得到:
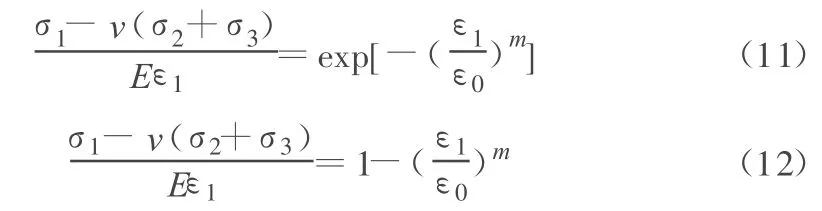
將式(11)兩邊取兩次自然對數,式(12)兩邊取自然對數,則有:
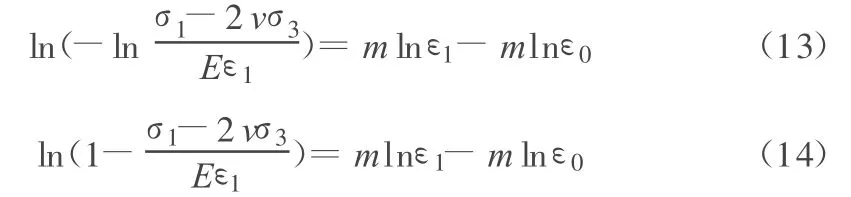
顯然,式(13)和式(14)為線性關系式。其中,m為直線斜率;-mlnε0為截距,則很容易將試驗數據通過線性擬合的方法求得m 和ε0。
2 損傷模型的驗證
為了對上面所建立的基于兩種分布的巖石損傷本構模型進行比較,引用文獻[9]的試驗資料對其進行了驗證分析。巖石彈性模量 E=90 GPa,泊松比υ=0.15,內摩擦角φ=31.303 9°。
將彈性模量E、泊松比υ及各圍壓下的試驗資料代入到式(13)和式(14)中進行線性化處理即可得到各圍壓下的分布參數m和ε0,分別如表1,表2所示。

表1 基于Weibull分布的模型不同圍壓時的分布參數值
將表1,表2中各圍壓時的分布參數 m,ε0以及實測試驗數據分別代入到式(6)和式(10)即可得到基于Weibull分布和冪函數分布的巖石破壞過程中的理論本構曲線。試驗曲線和本文兩種理論曲線的對比圖如圖1所示。

表2 基于冪函數分布的模型不同圍壓時的分布參數值
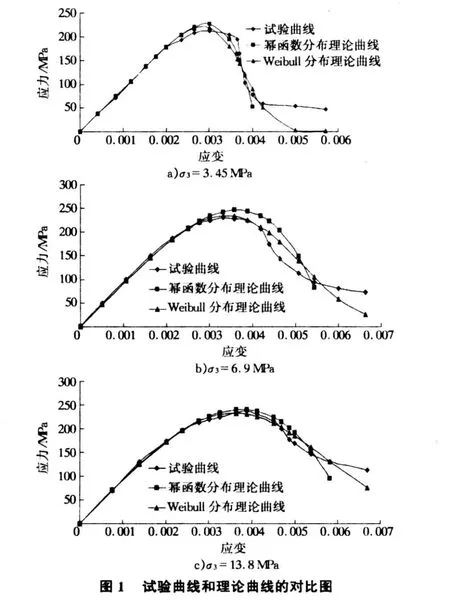
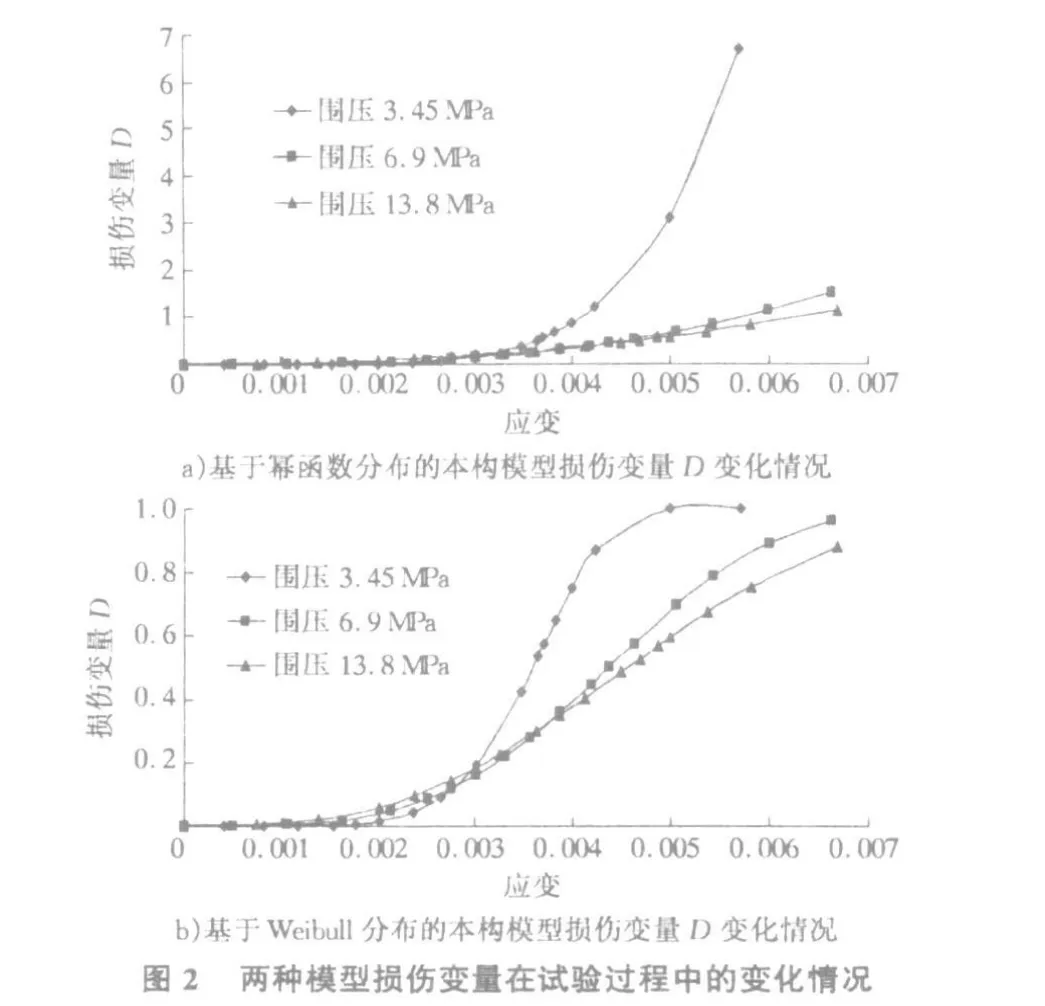
由圖1可以看出:在試驗前半部分,特別是在巖石變形的彈性階段,本文兩個模型的理論曲線均與試驗曲線有著較高的吻合度。而從塑性變形階段開始,兩個模型的理論曲線與試驗曲線之間的差別開始加大。但相比較而言,基于Weibull分布的模型曲線比基于冪函數分布的模型曲線與試驗曲線的匹配程度要好得多。特別是到試驗的最后階段,巖石強度接近于殘余強度的時候,基于冪函數分布的理論模型已經不能夠再反映巖石強度的變化情況。而基于Weibull分布的模型不會出現這種情況。巖石變形破壞過程中,兩種模型損傷變量D變化情況如圖2所示。
因此,從巖石變形破壞的全過程來看,基于Weibull分布的理論模型顯然要優于基于冪函數分布的理論模型。
3 結語
1)在巖石變形的彈性階段,兩個模型的理論曲線均與試驗曲線有著較高的吻合度;
2)從塑性變形階段開始,兩個模型的理論曲線與試驗曲線之間的差別開始加大。相比較而言,基于Weibull分布的模型曲線比基于冪函數分布的模型曲線與試驗曲線的匹配程度要好得多;
3)在巖石強度接近于殘余強度的時候,基于冪函數分布的理論模型的損傷變量D會出現大于1的情況,從而導致此時巖石強度的理論計算值出現負值,而基于Weibull分布的模型不會出現這種情況。
[1] 楊圣奇,徐衛亞,韋立德,等.單軸壓縮下巖石損傷統計本構模型與試驗研究[J].河海大學學報(自然科學版),2004,32(2):200-203.
[2] 唐春安.巖石破裂過程中的災變[M].北京:煤炭工業出版社,1993.
[3] 曹文貴,張 升.基于Mohr-Coulomb準則的巖石損傷統計分析方法研究[J].湖南大學學報(自然科學版),2005,32(1):43-47.
[4] 曹文貴,方祖烈,唐學軍.巖石損傷軟化統計本構模型之研究[J].巖石力學與工程學報,1998,17(6):628-633.
[5] 劉成學,楊林德,曹文貴.巖石統計損傷軟化本構模型及其參數反演[J].地下空間與工程學報,2007,3(3):453-457.
[6] 徐衛亞,韋立德.巖石損傷統計本構模型的研究[J].巖石力學與工程學報,2002,21(6):787-791.
[7] 許 江,李樹春,劉延保,等.基于 Drucker-Prager準則的巖石損傷本構模型[J].西南交通大學學報,2007,42(3):278-282.[8] 李樹春,許 江,李克鋼.基于初始損傷系數修正的巖石損傷統計本構模型[J].四川大學學報(工程科學版),2007,39(6):41-44.
[9] 耶格J C,庫克N G W.巖石力學基礎[M].中國科學院工程力學研究所,譯.北京:科學出版社,1983.

