MMF曲線擬合模型在固結系數計算中的應用

戴 韜

0 引言

固結系數是反映土層固結特性的參數,在基礎沉降計算中具有十分重要的意義。目前由室內固結試驗確定固結系數的方法中,應用最廣泛的是時間平方根法和時間對數法[1],這兩種方法均屬作圖法,人為因素對于固結系數的計算影響較大。此后,國內外許多學者提出了一些新的圖解法:試算法[1]、反彎點法[2]、司各脫法[3]以及標準曲線比擬法[4]等,但均無法回避圖解法缺點和求解不便。近期國內外學者通過對地基土體固結過程的研究,提出了一些新的方法,如包太[5]等提出的計算固結系數的最小二乘法、李濤[6]等提出的計算固結系數的剩余沉降對數法、張勇[7]等提出的計算固結系數的固結速率半對數法以及張儀萍[8]等提出的計算固結系數的方法等。其中,文獻[8]從太沙基固結理論出發,推導出了主固結沉降量與沉降速率之間的關系,且該關系為線性關系。利用這一關系計算固結系數非常簡便和實用,但文獻在確定各時刻的沉降速率時采用差商法,按式(1)計算:

顯然,按上式計算固結沉降速率即利用沉降曲線上某一段的割線斜率表示起點的切線斜率,也即用某一段時間的平均沉降速率代替起始點的沉降速率,誤差相對比較大。尤其當Δt越大時,其誤差也越大。

為了彌補這一方法的不足,本文采用沉降曲線擬合法來確定各時刻的沉降速率,進而按照文獻[8]提出的方法計算固結系數,并將計算結果與文獻的計算結果進行了對比。結果表明:用本文方法計算沉降速率,所得到的固結系數與文獻[8]相比,計算精度大大提高。

1 沉降量與沉降速率關系的推導[8]

土層固結度Ut的計算式為[1]:

其中,Cv為固結系數;t為時間;H為排水距離;m為奇數正整數。

由于上式級數收斂很快,當地基土層的固結度 Ut＞30%時,可近似取第一項,即:

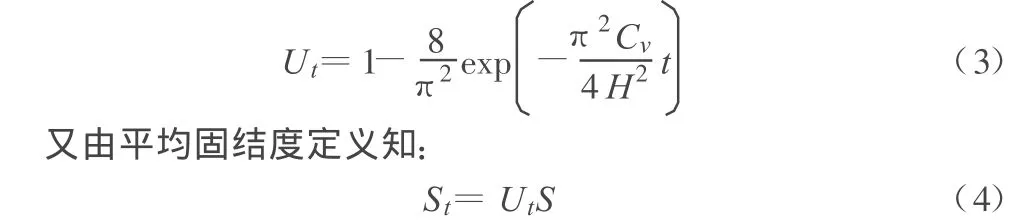
其中,St為土層某時刻的固結沉降;S為土層最終的固結沉降。

在某級試驗荷載下,β和S可以認為是常數。將式(5)對時間求導,有:

上式即為沉降速率的表達式。聯立式(5)和式(6)可得固結沉降量與沉降速率之間的關系式為:

顯然,式(7)中固結沉降量與沉降速率之間為線性關系,利用這一關系可以很方便的求解出固結系數Cv。

-β為直線段斜率,則固結系數表達式為:

因此,只要能夠準確的確定各時刻的沉降速率,即可得到β,進而得到固結系數 Cv。

2 沉降速率的確定方法

文獻[8]按照式(1)確定各時刻的沉降速率,顯然此種方法誤差相對比較大。尤其當Δt越大時,其誤差也越大。因此,本文采用MMF曲線擬合模型來擬合固結沉降量與時間之間的關系。一旦確定了固結沉降量與時間之間的關系,則很容易求得各時刻的沉降速率。

MMF曲線擬合模型的表達式為:

只要擬合值與實測數據之間的誤差足夠小,相關性足夠高,就可以用上式來描述土體沉降量與時間之間的變化規律,即:

其中,a,b,c,d均為模型參數。

則土體t時刻的沉降速率為:

利用式(11)即可計算出土體任意時刻的沉降速率,將各時刻的沉降速率與沉降量代入式(7)即可求出土體的固結系數。

3 算例驗證

算例[8]土樣初始厚度為16.5 mm,經24 h后土樣厚度為14.1 mm。試驗數據如表1所示。

表1 算例1試驗數據

根據表1中試驗數據,采用MMF曲線模型對沉降曲線進行擬合。擬合沉降曲線表達式為:

線性相關系數為:r=0.999 9。

擬合沉降速率表達式為:

擬合曲線如圖1所示。

由擬合曲線和誤差分析可知:用MMF曲線擬合模型對其進行擬合,誤差非常小,相關系數非常高,幾乎達到1。因此,MMF曲線模型能夠非常好的反映土體沉降與時間的關系,用式(13)得到的沉降速率非常接近土體固結沉降的真實速率。

由于固結系數在土體固結過程中并不是一個常數,而是不斷變化的。因此,固結系數的最終計算結果還與所取數據所處的時間段有關。取不同時間段的數據進行計算,所得到的固結系數也會有所不同。文獻[8]取540 s～2 160 s之間的數據計算固結系數,為了對比用式(11)計算沉降速率與用式(1)計算沉降速率對所得固結系數的影響,本文亦取540 s～2 160 s之間的數據計算固結系數。這樣可以避開其他因素的影響。

將表1中540 s～2 160 s之間的數據代入到式(13)計算各時刻的沉降速率。計算結果如表2所示。

表2 各時刻計算沉降速率表

將表2中各相關數據代入式(7),可得如圖2所示的曲線圖,其直線段斜率為β。

則直線段斜率β=0.001。線性相關系數 R=0.989 7,故沉降量與沉降速率之間具有較高的相關性。

土樣初始厚度為1.65 cm,在第 540 s時的厚度為 1.55 cm,在第2 160 s時厚度為1.481 cm,在此期間平均厚度為1.516 cm,則排水距離H=0.757 8 cm。

將 H=0.757 8 cm,β=0.001代入式(8),可得到固結系數Cv=2.33×10-4cm2/s。文獻[8]按照式(1)計算各時刻的沉降速率,計算得到的固結系數 Cv=1.722×10-4cm2/s。

由此可以看出,用相同的方法計算固結系數,只是確定各時刻沉降速率的方法不同,導致最終計算的固結系數具有較大的差別,誤差高達35%。因此,采用本文方法計算固結沉降速率,可使得最終得到的固結系數準確度得到大大提高。

4 結語

本文通過用MMF曲線擬合模型對地基土體固結過程中土體固結沉降量與固結時間之間的關系進行擬合,得到了各時刻比較準確的固結沉降速率,進而采用文獻[8]推導得到的速率法計算了土體的固結系數,并與文獻計算結果進行了對比。結果表明:采用本文方法計算固結沉降速率,可使得最終得到的固結系數準確度大大提高。因此,本文計算固結沉降速率的方法對采用速率法計算固結系數的方法具有一定的應用價值。

[1] 錢家歡,殷宗澤.土工原理與計算[M].第2版.北京:水利水電出版社,1996.

[2] Cour F R.Inflection point method for computing Cv[J].Journal Soil Mechanics Foundation Engineering,ASCE,1971(1):827-831.

[3] Scott R E.New method of consolidation coefficient evaluation[J].ASCE,1976(1):29-39.

[4] 李金軒,胡金珠.確定固結系數的標準曲線比擬法[J].工程勘察,1996(1):21-22.

[5] 包 太,劉新榮,朱 凡,等.固結系數的最小二乘法計算[J].巖土工程學報,2005,27(10):1230-1232.

[6] 李 濤,張儀萍,曹國強,等.推算室內固結系數的剩余沉降對數法[J].巖土工程學報,2003,25(6):724-726.

[7] 張 勇,孔令偉,白 冰,等.確定固結系數的固結速率半對數法[J].巖土力學,2007,28(2):355-358.

[8] 張儀萍,俞亞南,張土喬,等.室內固結系數的一種推算方法[J].巖土工程學報,2002,24(5):616-618.