ISO荷載模式下紹興路跨線人行橋動力響應分析及舒適性評估

陳階亮，費正云，黃 毅

（杭州市七格污水廠工程建設指揮部，浙江杭州310005）

1 工程概況

跨線橋工程位于杭州市東新路與紹興路交叉口，橋梁與道路夾角為60°左右，南北向的東新路和東西向的紹興路均為城市主干道，車流量大，屬杭州市區通行較繁忙的交叉口。為了解決交通車輛通行和滿足行人穿越道路問題，在東新路整治工程中跨線橋工程和人行天橋設施同步實施。紹興路口跨線橋的主橋跨組成為3×30 m+（50+70+50）m+3×30 m=350 m，橋面橫向布置為 0.5 m（防撞欄桿）+7.25 m（行車道）+0.5 m（防撞欄桿）+7.25 m（行車道）+0.5 m（防撞欄桿）=16 m。第一、三聯上部結構為等截面預應力混凝土連續箱梁，第二聯上部結構為等截面鋼箱連續梁。圖1為跨線橋斷面及連接示意圖。

跨線橋為一座結構獨特的人行橋梁，人行橋的主跨為輕型雙主梁格構結構，主梁通過豎、斜吊桿懸掛于上跨的行車道橋梁底，主梁的兩端部擱置在引道橋伸出的牛腿上；S型引道橋采用等高度的鋼箱梁連續結構，引道橋的橋墩采用單鋼管或雙鋼管柱，與主跨橋交接處一側通過牛腿與行車道橋的橋墩相連，另一側通過豎吊桿懸掛于行車道橋主梁上。采用大型通用有限元計算軟件ANSYS，建立了跨線人行橋的有限元分析模型。采用空間梁單元beam4模擬行車道主橋、人行主橋、人行引道橋及橋墩結構，而采用桿單元link8模擬豎、斜拉吊桿。為了協調行車道主橋梁單元和人行主橋梁單元之間的關系，將行車道主橋模擬為帶剛臂魚骨形模型。另外為提高計算精度，人行橋主跨采用更為精確的縱梁與橫梁組成的梁格體系。全結構共有581個節點，667個梁單元，44個桿單元。跨線人行橋的有限元模型如圖2所示。

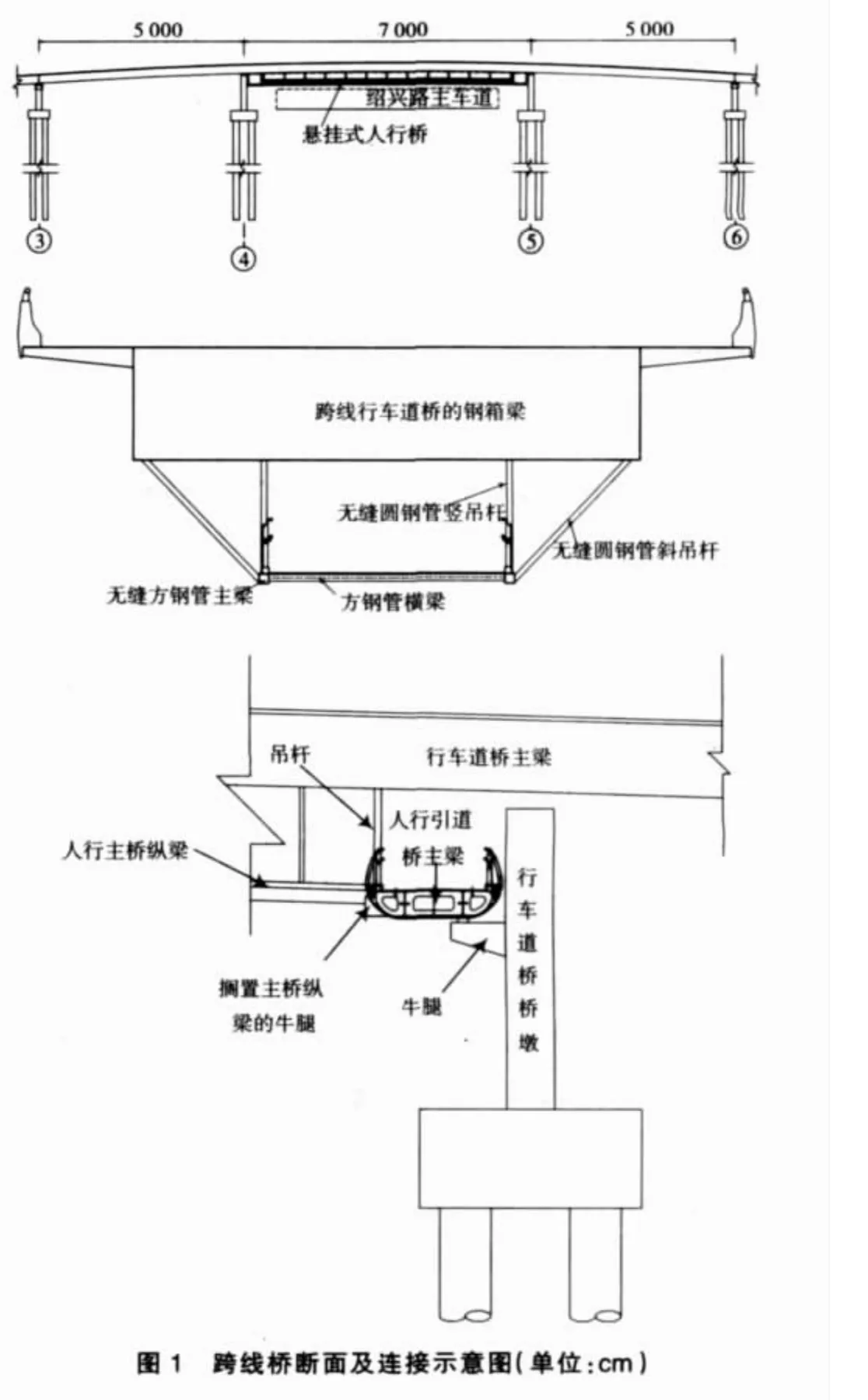
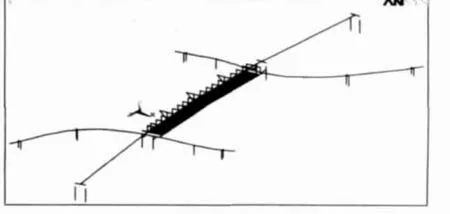
圖2 跨線橋動力分析有限元模型

2 依據ISO的結構響應分析及舒適性評估

行人行走過程中不僅會在橋上產生激勵荷載，而且人－橋之間會發生相互耦合作用。行人激勵下的橋梁結構的振動響應由振動方程計算得到：

式（1）中：M——結構的質量矩陣；

K——結構剛度矩陣；

C—結構阻尼矩陣；

R——行人激勵產生的動力荷載。

ISO規范中評判人行橋舒適性的指標也采用均方根加速度aRMS，因此在分析了紹興路口跨線人行橋各結構的加速度響應時程的基礎上，仍選取了穩態部分的10個周期內響應進行分析。

ISO規范在人行橋振動舒適性評價方法更為全面，不僅規定了單人荷載模式，而且考慮了步伐非一致及同步伐的人群荷載，既規定了行人激勵下的豎向荷載，也規定了行人激勵下的橫向荷載。ISO所規定的各種行人激勵荷載如下：

單個行人的豎向荷載模式為：

單個行人的橫向荷載模式為：

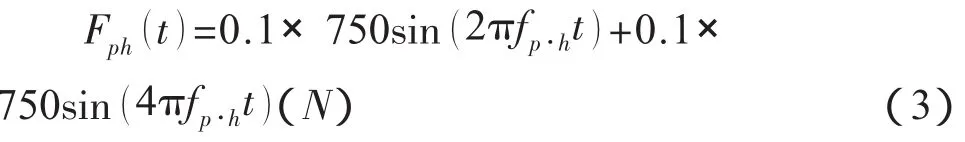
人群非一致步伐下的豎向荷載模式為：

人群非一致步伐下的側向荷載模式：

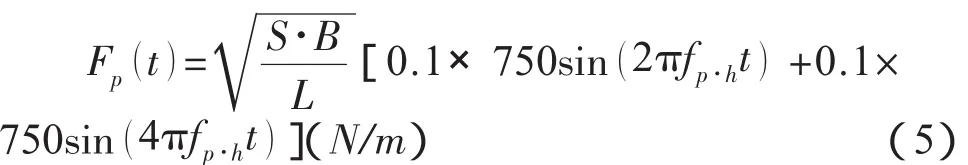
人群同步伐下的豎向荷載模式：

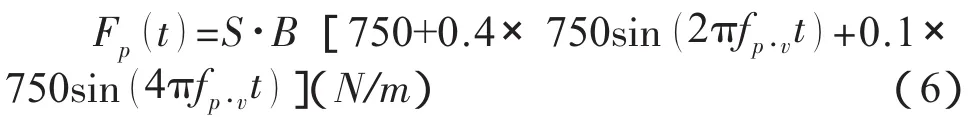
人群同步伐下的側向荷載模式：

式（2）～式（7）中：fp·v、fp·h——是行人豎向和側向的步伐頻率，為求得最大的振動響應，該頻率分別取結構的前幾階豎向和橫向固有頻率；

S——人群密度，本文取S=1人/m2；

B——人行橋的寬度，人行主橋的B=5 m，引道橋的B=3 m；

L——人行橋的計算跨徑，主橋的計算跨徑LZ=60 m。

ISO規定，在求解人行橋在單個行人荷載激勵下的振動響應時，荷載須作為集中荷載作用在容易引起最大響應的位置處（如跨中截面處）。當求解步伐非一致或同步人群荷載激勵下響應時，荷載須作為均布荷載分攤到能引起最大響應的結構跨上。

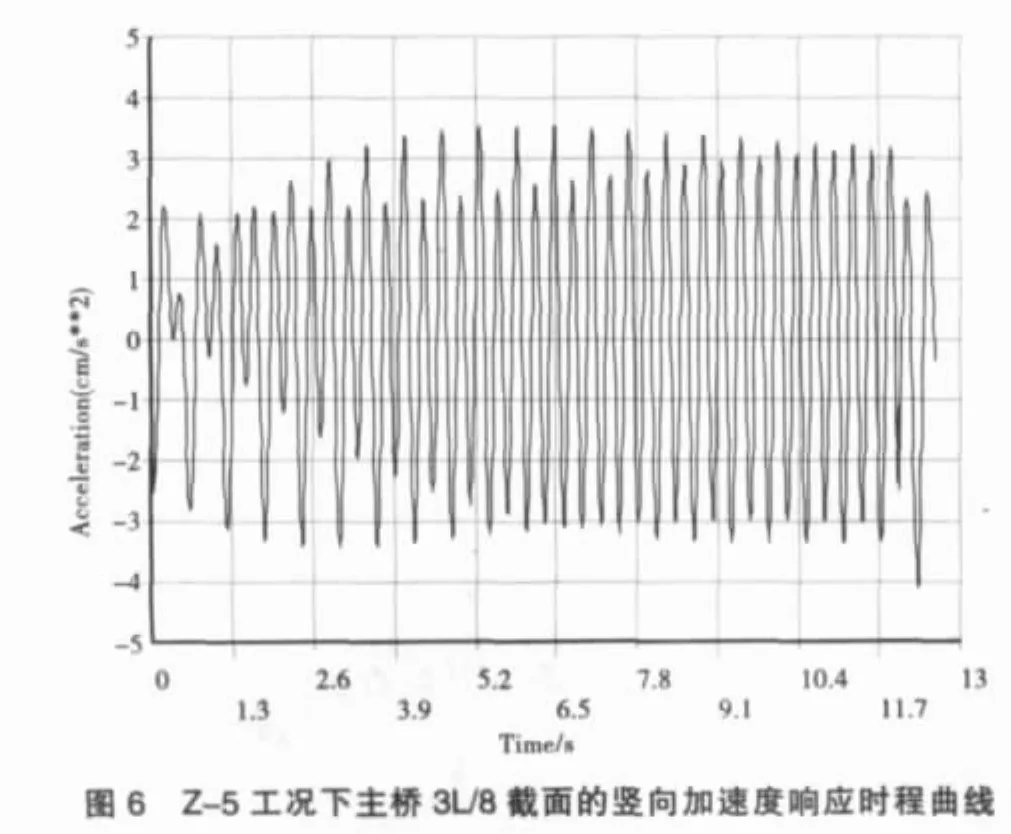
ISO的第10137條還專門針對人行橋給出了行人運動過程中滿足振動舒適性的臨界曲線，如圖3所示，當結構的振動加速度有效值在圖中實線以下時認為結構滿足舒適度要求。但是，該規范還強調，當行人靜止于人行橋上時，其舒適性的臨界指標值要適當降低，僅為行人運動中舒適性指標值的一半。表1為依據ISO確定人行橋主橋舒適性分析荷載工況。圖4～圖11為各工況下主橋不同截面豎向、橫向加速度響應時程曲線。

表1 依據ISO確定人行橋主橋舒適性分析荷載工況

3 結論

（1）行人步伐頻率與結構的固有頻率一致所引起的振動響應要遠大于兩者不一致時的振動響應；對于人行主橋來說，第一階豎彎頻率激勵下產生的振動響應最大，第三階次之，而第二階最小。

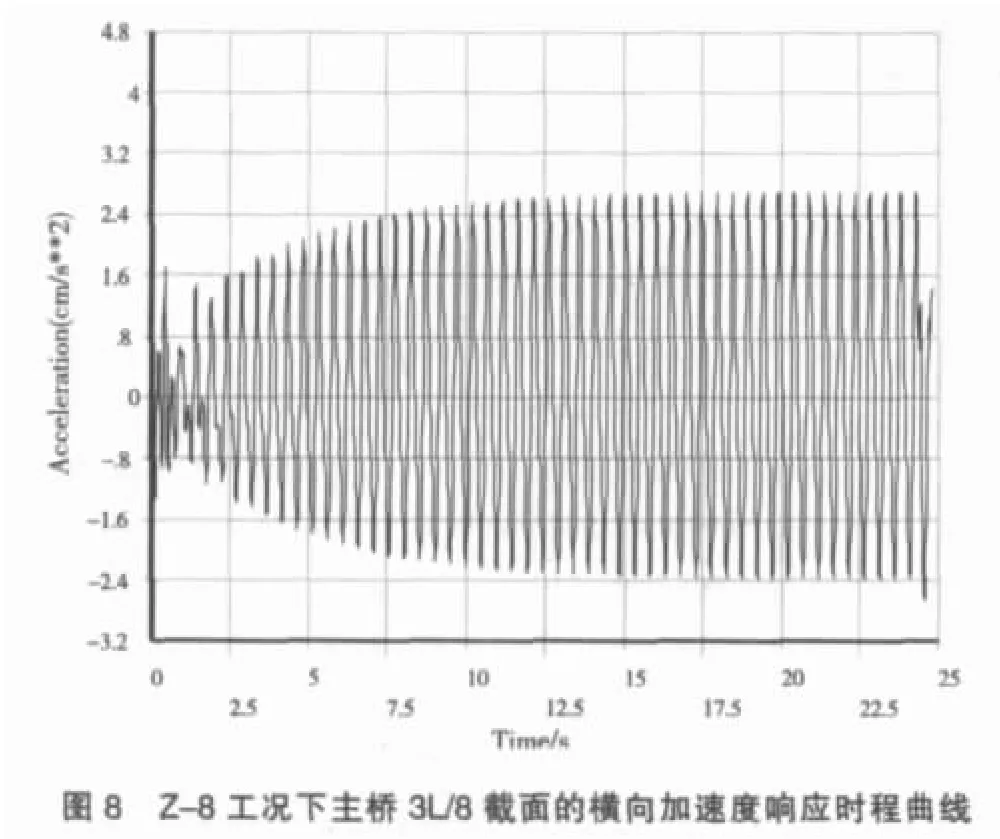
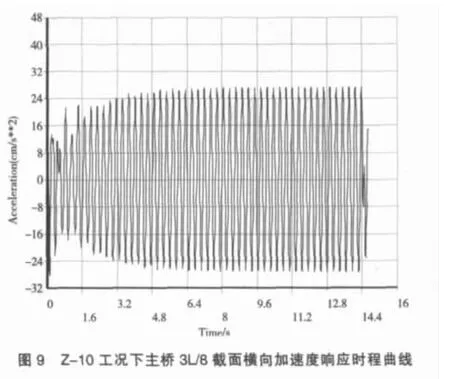
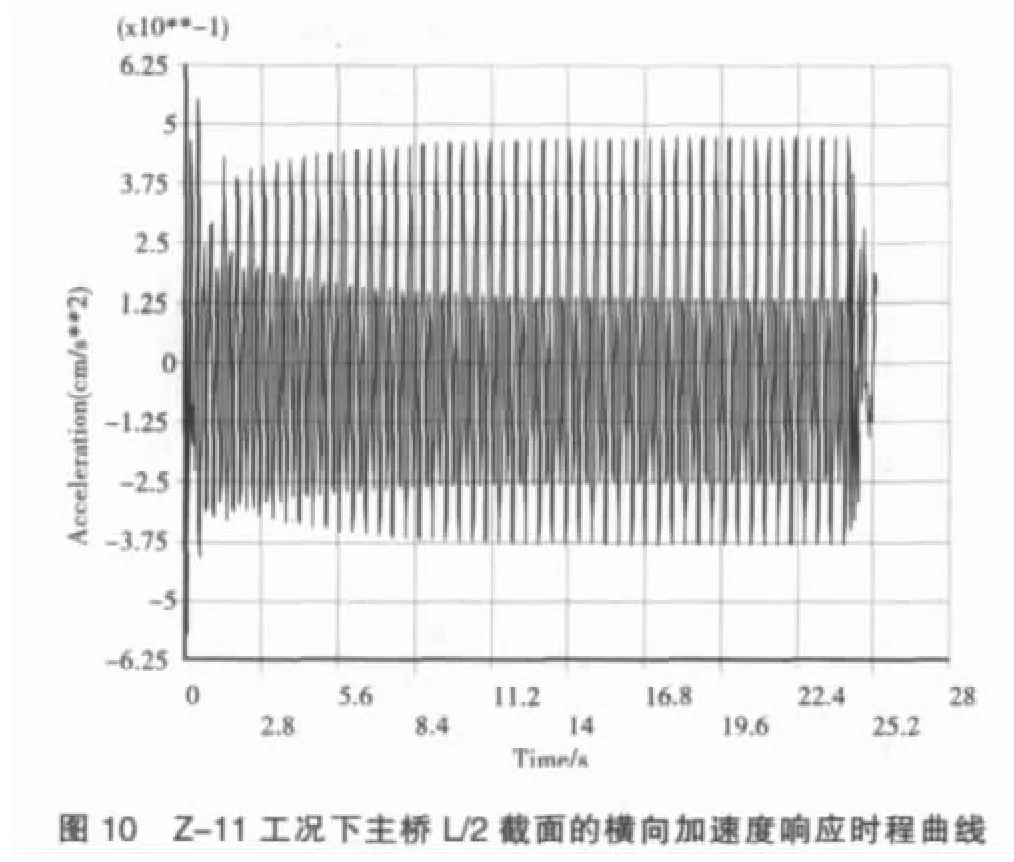
（2）跨線人行橋在單個行人或非一致步伐的人群以任意步頻通過人行橋時，產生的豎向和橫向加速度響應均能滿足舒適度的要求；但當人群同步伐（頻率相同、相位相同）通過人行橋時，人行橋將會產生非常大的振動響應，其使用舒適性將取決于人群中的行人數量（人群密度），因此從結構安全性和使用舒適性等方面考慮，人行橋在使用過程中要盡量避免多人齊步跑通過橋梁。

[1]ISO,Bases for design of structures Serviceability of buildings and pedestrian walkways against vibration,ISO/CD 10137,International Stadardization Organization,Geneva,Switzerland,2005.

[2]范立礎.橋梁抗震[M].上海:同濟大學出版社,1996.

[3]朱伯芳.有限單元法原理與應用（第二版）[M].北京:中國水利水電出版社,1998.