湯旺河流域主要測站年徑流量隨機性與趨勢性分析
肖鵬云,李敬東,田長濤
(1.佳木斯水文局,黑龍江 佳木斯 154002;2.伊春水文局,黑龍江 伊春 153000)
1 前言
在實際工作中,為了進一步分析、預測某一水文要素的變化規律,經常會建立一些水文數據分析、模擬數學模型。在根據隨機水文學原理和分析技術對水文要素系列數據建立分析模型時,為了了解資料系列有無明顯的系統性影響和趨勢性的存在,要對數據系列進行必要的隨機性和趨勢性檢驗,然后才能建立數據分析模型。本文以湯旺河流域控制面積較大的5個主要測站為例來分析各站年徑流量數據的隨機性和趨勢性特征,各站資料系列情況見表1。
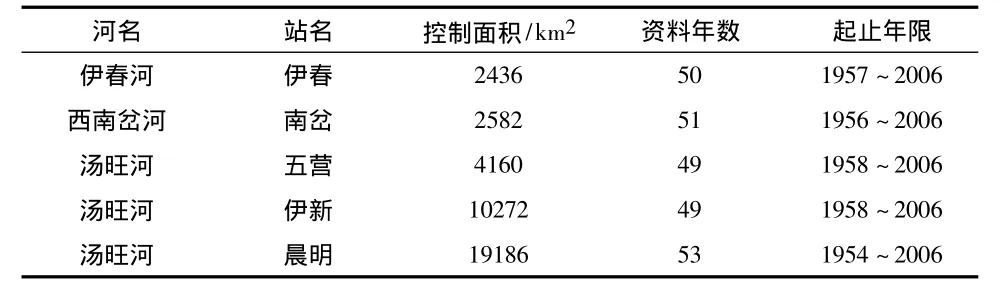
表1 選用測站一覽表
2 資料系列隨機性的統計檢驗
隨機性的統計檢驗通常采用轉折點檢驗法。本法是檢查數據系列高值和低值(相對于鄰值而言)的個數。在實測系列 Xt(t=1,2,…,n)中,如果 Xi大于 Xi-1和 Xi+1或小于兩相鄰值,則在t=i處出現轉折點P。對于3個不等的觀測值,這種數量次序的6種可能情況是:
①Xi-1>Xi>Xi+1;②Xi+1>Xi>Xi-1;③Xi>Xi-1>Xi+1;④Xi+1>Xi-1>Xi;⑤Xi>Xi+1>Xi-1;⑥Xi-1>Xi+1>Xi。
在隨機系列中,6種情況具有相同的出現概率。除了①、②之外,轉折點均可出現,其出現的可能性是2/3。因為轉折點不可能出現在t=1和t=n處,因此隨機系列中轉折點的期望個數為:
E(p)=(n-2)×2/3。同時可證明轉折點P的方差為:Var(P)=(16n-29)/90;所以,P可以標準化,即Z=[P-E(P)]/[Var(P)]1/2近似為標準正態變數[1]。
由于太多或太少的轉折點表明為非隨機性,所以采用雙尾的顯著性檢驗,顯著性水平設為5%,相應的判別標準值為-1.96~1.96。各站資料的隨機性檢驗計算結果(參見表2)表明,各站Z值均在判別標準范圍內。從而表明,各站年徑流量系列中具有隨機性的原假設在5%的顯著性水平下不能拒絕,即表示實測資料系列具有一定的隨機性。
3 資料系列趨勢性的統計檢驗
趨勢性的統計檢驗采用肯德爾(Kendall)的秩次相關法,此檢驗也稱τ檢驗,是以連續觀測值超過某特定值的個數(記為P)的一種檢驗。例如,某水文要素系列X1,X2,…,Xn,假定它是連續增加的(上升趨勢),那么,先以X1為比較特定值,其右邊值大于X1的有n-1個,再以X2為比較特殊值,其右邊的值大于X2的有n-2個,余此類推,可以得到以X3,X4,…,Xn-1為比較特定值時,其右邊值大于 X3,X4,…,Xn-1的個數分別為n-3,n-4,…,1。這樣得到總數 p=(n-1)+(n-2)+…+1=(n-1)×n/2。如果系列值全部倒過來,則p=0。由此可知,對于無趨勢的系列,E(p)=(n-1)×n/4。趨勢性檢驗的基礎是統計量:τ=4P/[n(n-1)]-1。對于隨機系列有:E[τ]=0,亦可證明:Var(τ)=[2(2n+9)]/[9n(n-1)],且 Z= τ/[Var(τ)]1/2,Z 在 N 增加時很快收斂于標準者正態分布[2]。
趨勢性檢驗的顯著性水平設為5%,相應的判別標準值為“-1.96~1.96”。各站資料的趨勢性檢驗結果(參見表3)表明,伊春、南岔、伊新三站年徑流量無趨勢性的原假設在5%的顯著性水平下不能拒絕。至于五營、晨明沒有通過趨勢檢驗的測站,可由P是否接近(n-1)×n/2或0兩種極端情況來做進一步檢驗判斷[2]。五營站n=49,p=(n-1)×n/2=1176,表3中實際p=385。晨明站n=53,p=(n-1)×n/2=1378,表3中實際p=521。兩站的實際p,既不接近(n-1)×n/2,也不接近0這兩種極端情況。說明其上升或下降趨勢不十分明顯,仍可將其劃歸于無明顯趨勢之列。
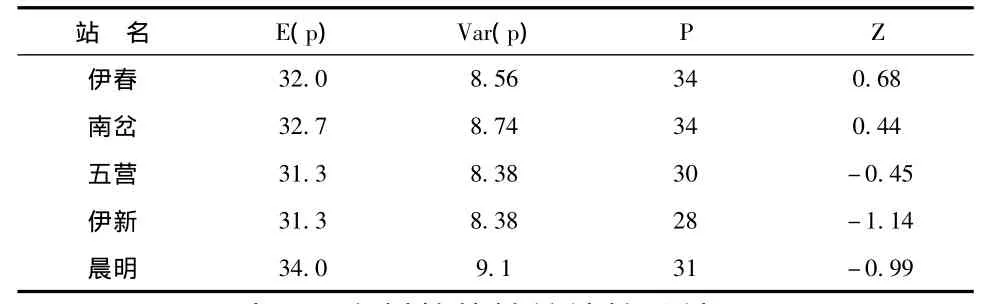
表2 資料隨機性統計檢驗結果
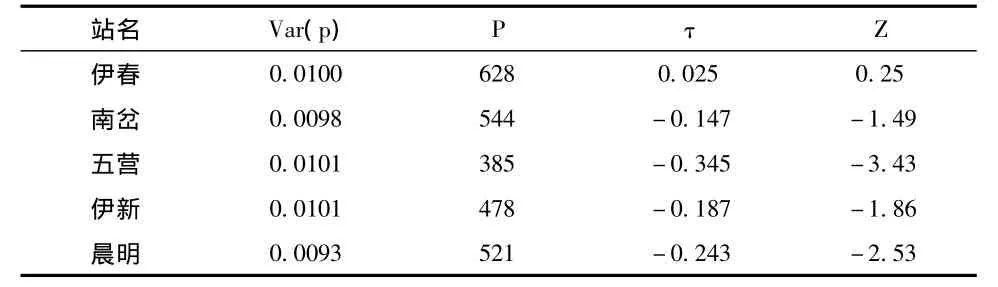
表3 資料趨勢性統計檢驗結果
由于五營、晨明兩站徑流量系列數據沒有通過顯著性水平為5%的趨勢性檢驗,僅通過p接近兩種極端情況程度檢驗;因此在實際建立數據擬合模型時要考慮其模糊趨勢性對擬合精度的影響。對完全通過隨機和趨勢性檢驗的數據,也要對其擬合模型參數的靈敏度、合理性、可靠性進行充分的率定和檢驗,防止出現虛假擬合現象。
[1] 金光炎.隨機水資源技術[M].北京:農業出版社,1987.
[2] 金光炎.水文統計原理與方法[M].北京:中國工業出版社,1964.

