用戶出行費用綜合更新自學習模型的研究

賀振歡

(北京交通大學軌道交通控制與安全國家重點實驗室,北京100044)

He Zhenhuan

(State key Laboratory of Rail Traffic Control and Safety,Beijing Jiaotong University,Beijing 100044,China)

用戶出行費用是指用戶對出行過程中所付代價的一種綜合評估,是用戶出行過程中進行路徑選擇的主要依據。因此,研究和描述用戶出行費用更新的機理對于路徑選擇等相關研究具有重要理論意義,進而也會對交通管理及ITS等相關研究產生重要影響。用戶對于出行費用的判斷往往要受到多方面的影響,導致其對于出行費用的估計會不斷變化。為此,研究人員提出了均衡模型[1]、近期調整模型[2]、權重模型[3]等,從不同方面反映了行人對出行費用的估計及學習行為。但這些模型或多或少都存在一定的局限性,不能全面地反映出行者對于路徑費用的認知和學習過程。因此,本文將綜合上述各模型的優點構造新的學習模型。

1 費用估計模型

影響用戶對于出行費用判斷的因素很多,除當前交通流信息的影響外,用戶往往還要受到以往路徑選擇及其走行結果的影響,其原因在于出行者會不斷地從以往的出行結果中獲取和更新關于路徑出行費用的相關信息,并據此調整路徑費用的判斷[1-4]。此外,路網的固定信息(如路徑長度及自由流速度)也是影響路徑費用的重要因素。因此,出行者對路徑出行費用的估計要受到當前車流信息、出行經驗信息和固定信息3個方面信息的影響。路徑是由若干路網單元(包括路段和交叉口)組成,因此可將路徑費用分解為若干路網單元的費用。出行者j對路網單元a當前費用的估計模型可描述為

根據路徑選擇的依據不同,路網中出行者一般可分為3類:臨時型、經驗型和固定型。模型中個參數標識出了出行者j路徑選擇過程中對各種信息的依賴程度,調整3個參數的大小即可使模型滿足對不同類型的出行者進行描述的要求。當時,模型描述的是臨時出行者的費用估計行為,該類出行者主要依賴當前路網車流信息做出行決策;當時,模型則轉變為完全經驗型出行者的出行決策行為描述,這類出行者對路網每日的車流情況非常熟悉,主要依據長時間積累的出行經驗進行路徑費用的估計;而當時,模型又變為對完全固定型出行者的決策描述,該類出行者對路網極不熟悉,只能依靠從地圖上獲取的靜態信息進行出行決策。

2 出行費用自學習原理分析

現有的自學習模型主要描述經驗費用的學習過程,實際上出行者隨著經驗的增加,出行者在費用估計時對各種信息的信賴程度也在不斷變化之中,即αaj,βaj,γaj也不斷變化之中。因此,本文提出綜合更新自學習模型,以當前費用估計為核心,將出行者的費用估計和學習過程分為當前費用估計、經驗費用學習和權重調整3個部分[2,5,6],并建立相應模型。當前費用估計模型主要用于將經驗費用與當前車流分布等實時信息以及部分固定信息相結合,產生新的估計費用。權重調整模型主要是根據出行者對網絡的熟悉程度不同而調整各項信息在當前費用估計時所占的比重。經驗費用更新模型主要描述用戶每日估計費用的變化規律。該模型綜合了歷次出行經驗對用戶出行費用預測的影響,并以權重調整模型為基礎對路徑經驗費用進行滾動式更新。

上述3個模型并不是完全獨立的,而是互為基礎、互相影響。首先,出行者在出發前估計當前費用,并據此選擇合適的出行路徑;其次,隨著出行次數的增加,出行者對網絡熟悉程度的增加,費用預測模型中的權重參數要發生變化;同時,出行結束后,出行者要根據本次出行的實際費用對出行經驗值進一步更新。整個過程如圖1所示。

圖1 基于自學習的費用估計過程

當前費用估計模型包含了同時影響出行者當前費用估計的3種信息,而這些信息進一步又可歸為兩類:實時費用信息和非實時費用信息(包括經驗信息和靜態信息)。實時費用信息系數的值主要與出行者個人習慣及其受誘導系統的影響的程度有關,可令其中M為根據個人特性而確定的常數。在無誘導系統的情況下,出行者只能根據所處路網單元的車流狀況大致推斷路網中當前車流信息,所獲信息的準確度較低,對該信息的信賴程度也很小。

3 調整模型

3.1 權重調整模型

在實際出行過程中,隨著出行者經驗的增加,對經驗費用的信賴程度也在不斷變化,使權重也相應發生改變。一般出行過程中途經路網單元a次數越多,出行者對其熟悉程度就越高,也就越信賴于經驗值進行費用估計,相應地值就越大而的值越小,反之亦然。若出行者未受到誘導系統的影響,當其對路網單元a的選擇次數n=0時,出行者無任何經驗,此時道路費用估計主要信賴于固定信息,因此隨著出行次數的增加,出行者經驗增加,使出行者在費用估計過程中對固定信息的信賴程度迅速降低,因而值迅速下降,而同時值迅速上升。但隨著出行次數的進一步增加,若路網及交通管制措施未發生較大變化,則出行者的經驗值會逐漸接近于實際情況,變化較小,此時值會相應逐漸趨于穩定,特別是當權重隨出行次數的變化特征如圖2中曲線a,b所示。

本文嘗試用負指數函數來擬合權重 γaj隨路網單元被選擇次數而變化的過程,即

由于不同城市路網車流狀況的穩定性及出行者個人特性等原因,不同的出行者的權重變化曲線會有所不同。因此,模型提出了調節系數 θ,用于調節出行者權重變化的速度,該值需通過對不同城市或不同類型出行者調查統計后確定。

圖2 費用估計系數變化曲線

另外,歷史車流信息是有一定有效期的,出行者只會被最近一定時間內的信息所影響。因此,模型2中的參數 n實際上應為最近D天內出行者選擇單元a的次數。這樣,實際上并不是單調遞減或遞增的,而是會隨著出行者選擇行為變化大小。

綜上所述,可得3種權重的變化調節模型為

3.2 費用調整模型

每一次出行結束后,出行者都要根據本次出行的實際情況更新其經驗費用,本文將綜合目前較為常用的權重模型和近期調整模型的優點,采用預測時間與實際走行時間的偏差對費用經驗值進行修正,同時利用權重模型能有效反映出行者不斷學習、調整認識的連續過程這一特性構造新的費用學習更新模型。由于出行者的經驗值與此次出行之前的經驗值相關,同時會按本次出行延誤時間對經驗值進行調節。因此,出行后的經驗值更新模型可描述為

其它參數同前。

上述3個模型通過出行前的經驗學習及融合、出行后經驗更新以及權重調整幾個過程,比較完整地描述了道路估計費用的演變,從而更加完整、準確地反映了出行者的對路徑費用的學習和更新過程。

4 綜合學習模型

上述自學習模型描述了出行者對任一路網單元進行學習的過程。實際上,由于城市路網規模巨大,出行者不可能對路網中所有的單元都逐一學習并獲取經驗值。通常,出行者只能記住那些最近一段時間內經常發生擁擠的路網單元的歷史信息。若用表示路網單元a在出行者j最近第n天途經時是否發生擁擠(在本文研究中,“擁擠”主要參考HCM手冊中服務水平定義,服務水平為E級以下為擁擠),1表示發生擁擠,0表示沒有,則出行者j歷史經驗學習對象集合可表示為

式中:E為出行者學習時效長度,即多少天以內的經驗對用戶是有效的;wj為出行者j的學習標準,只有某路網單元擁擠頻率達到這個標準后,出行者才會開始相應歷史費用的學習;L和N分別為路段和交叉口集合。

因此,可將經驗值更新模型(式4)改進為

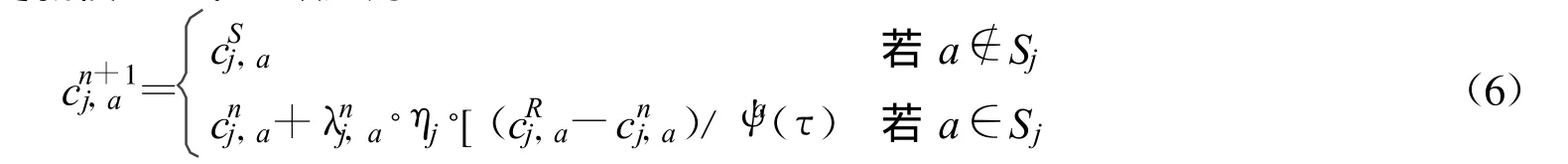
同樣,權重調節模型(式3)實際上也是相對于集合Sj中的單元而進行的,而對于?a?Sj,出行者進行費用估計時基本不會考慮經驗費用,則此時該模型應描述為

上述學習過程是針對每個出行者而言,這樣系統需要建立每一個出行者的出行費用及權重系數矩陣,當系統中出行者較多時,這種方式顯然不太可行的。因此需要對學習過程進一步簡化:將路網劃分為若干OD小區,將從同一個小區出發到另外同一個小區的出行者歸結為一類,對每一類分別進行自學習過程。該簡化方法主要出于如下考慮:首先,相同類別的出行者出行過程中所經過的區域有很大一部分應該是相重合的;其次,對于出行歷史時間影響較大的是擁擠現象,而擁擠現象通常會在一定范圍內傳播,即使出行者在當日出行中未選擇擁擠路網單元,也會對一定區域內的擁擠狀況有所了解。因此,對于同一類的出行者來說,其出行經驗會大致相同,可近似地用同一個經驗值及權重系數來表示。這種處理方式在保證一定精度的同時又能大大簡化實際處理過程。

按上述方法進行自學習時,具體的小區劃分方法及出行者分類精度應根據模擬實驗要求及實驗條件來確定。而每一類的當日出行費用值則可由該類中每一個出行者的出行費用轉化為高峰時段費用后取平均值。

5 算例

根據上述模型,相應的仿真系統已被開發,并對4×4路網進行了仿真研究。仿真過程中,行人的路徑選擇主要采用Logit模型,并直接采用走行時間作為出行費用。仿真過程中,用戶學習率統一設為25%;θ取0.1以保證約30日后相關路徑的費用估計主要由經驗費用和實時費用來決定;M取0.2。仿真過程中某路段的實際平均走行時間與經驗估計時間變化如圖3所示。

圖3 某路段實際走行及經驗時間變化圖

從圖3可以看出,經過一段時間學習后,路段經驗費用的變化趨于平穩,并與整個路段的實際平均費用相接近。同時,整個路段的實際平均走行費用變化幅度也相應縮小,說明用戶經過學習后,能較真實地評估走行費用,使路網中用戶的出行分布更加均衡。

6 小結

提出了出行費用估計的綜合更新自學習模型,將當前費用估計歸結為實時費用、經驗費用以及固定費用3種信息共同作用的結果。在描述經驗費用自學習過程的同時,提出上述3種費用的權重也在不斷學習變化之中,并提出相應權重調整模型。上述3種模型集出行前的費用估計、出行后經驗更新以及權重調整幾個過程為一體,形成比較完整的路徑費用學習演變過程。

[1]HOROWITZ J L.The stability of stochastic equilibrium in a two-link transportation network[J].Transportation Research Part B,1984,18(1):13-28.

[2]HANI S M,CHANG G L.Experiments with departure time choice dynamics of urban commuters[J].Transportation Research Part B:Methodological,1986,20(4):297-320.

[3]RICHARD HM,EMMERINK,et al.The potential of information provision in a simulated road transport network with non-recurrent congestion[J].Transportation Research Part C,1995,3(5):293-309.

[4]MOSHE B A,ANDRE D P,ISAM K.Dynamic network models and driver information systems[J].Transportation Research Part A,General,1991,25(5):251-266.

[5]ZHOU X S,HANI SM,ZHANG K L.Dynamic micro-assignment modeling approach for integratedmultimodal urban corridor management[J].Transportation Research Part C,Emerging Technologies,2008,16(2):167-186.

[6]曲衛民.交通流模擬體系中用戶出行路徑選擇模型的探討[J].北方交通大學學報,2004(3):44-4.