多孔徑發(fā)射對大氣激光通信系統(tǒng)誤碼率的影響

黃俊森

（桂林電子科技大學 廣西 桂林 541004）

近年來，隨著激光通信技術的日漸成熟，近地面大氣激光通信再度成為研究熱點，該技術不僅是下一代光通信技術的發(fā)展方向之一，同時也是寬帶網絡接入中解決“最后1公里”問題的最佳方案。但由于受大氣湍流影響，現階段大氣激光通信系統(tǒng)的可靠性與穩(wěn)定性在實際應用中會嚴重降低，特別是大氣湍流效應中的光強閃爍會極大地增加系統(tǒng)的誤碼率。雖然大氣信道的特性無法改變，但可以改進收發(fā)系統(tǒng)，而大量理論分析和實驗表明[1]：多孔徑發(fā)射技術是減弱大氣湍流影響的有效途徑，目前已越來越多地應用于以大氣為傳輸媒質的空間激光通信系統(tǒng)中。

1 理論分析

單個激光光束通過弱起伏湍流大氣后的大氣閃爍概率分布服從對數正態(tài)分布，光強起伏的大小可依據Rytov近似理論較好地預測[2]。而對于方差飽和閃爍區(qū)域，從理論上證明光強起伏服從負指數分布，并得到實驗驗證[3]。實驗結果還表明，強起伏湍流大氣中或長距離傳輸時，若傳輸距離l和發(fā)射鏡間距r滿足一定條件，隨著光束數目n的增加，大氣閃爍將趨于對數正態(tài)分布，而不是負指數分布，這說明閃爍分布與傳輸距離l、光束數目n、發(fā)射孔徑間距r等有關。

對于通信系統(tǒng)，為保證接收端能落在發(fā)射光束之內，發(fā)射光束的發(fā)散角不會很小。發(fā)射光束到達接收端時，光斑尺寸通常比接收孔徑大很多。因此，用平面波近似是可行的。而在實際激光通信系統(tǒng)中，從發(fā)送端發(fā)出的激光經光學透鏡準直后確實可當作平面波處理。

Tartaskii運用Rytov近似給出激光通過大氣后的接收光強起伏（即光強閃爍）的理論模型[4]，在弱起伏條件下，根據此模型得出水平傳輸時的對數振幅方差為[5]：

則：

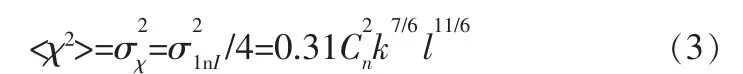
對于數字激光接收系統(tǒng)，光接收機接收光信號時，其誤碼率為[6]：

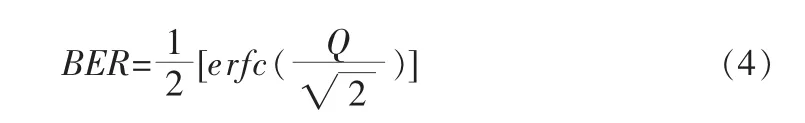
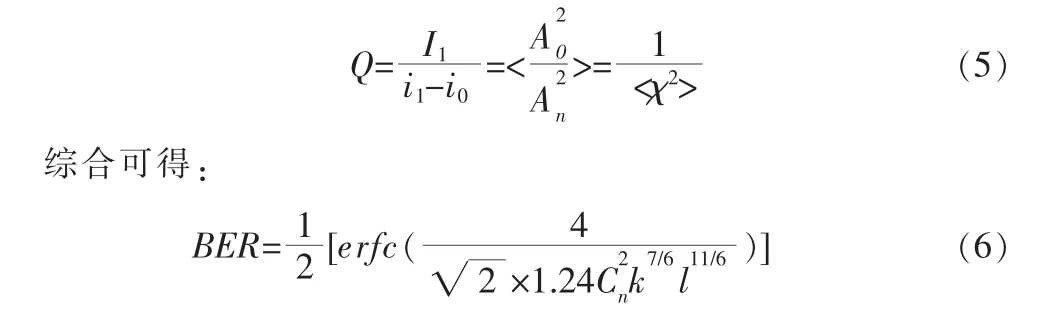
如果大氣信道間距r＞＞r0，則n束光在接收面上的對數幅度起伏互不相關，其疊加后的光強起伏方差為：

考慮到設備的機動性能及探測器的實際大小，n束光完全不相關的幾率不大，所以必須考慮各光束之間的相關性對光強起伏的影響。為簡化分析，假設各光束之間間距相等且對稱分布，則疊加后的光強起伏方差為[6]：

式中，n是發(fā)射孔徑數目，γ為歸一化相關系數。

則多孔徑發(fā)射的誤碼率為：

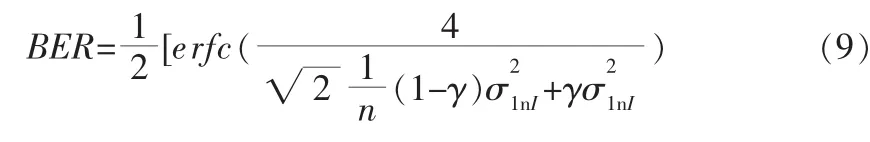
2 計算結果和仿真

圖1所示是在波長為850 nm，大氣折射率結構常數C2n為5×10-14，相關系數為0.5時，發(fā)射孔徑數目不同，誤碼率與傳輸距離之間的關系曲線。由圖1可以看出，通過多發(fā)射機發(fā)射可以改善系統(tǒng)的誤碼率。湍流強度一定時，多孔徑的誤碼率比單孔徑降低了幾個數量級。同時，隨著發(fā)射孔徑數目增加，誤碼率的變化越來越小。

圖2表示波長為850 nm，發(fā)射孔徑n為8，相關系數為0.5時，誤碼率隨大氣折射率結構常數和傳輸距離的變化關系，可以看到傳輸距離相同時，湍流越強，則誤碼率越大，隨著湍流強度的增大，誤碼率增加變快，當光波傳輸到一定距離時誤碼率增加很快。

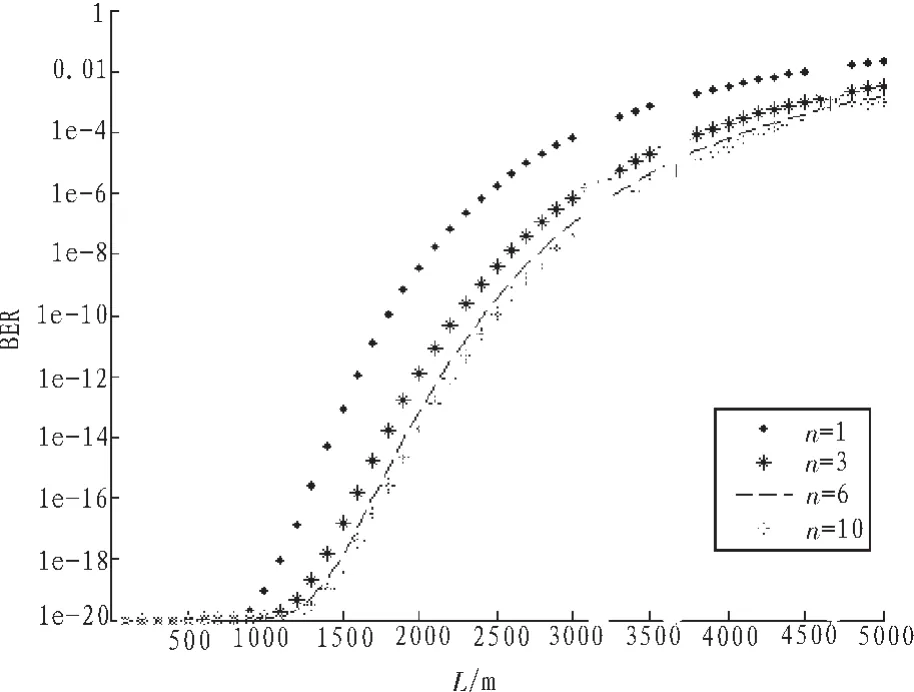
圖1 誤碼率與孔徑數目n的關系

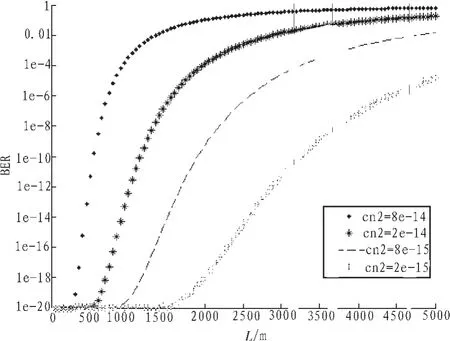
圖2 誤碼率C2n與和L傳輸距離的關系

圖3為大氣折射率結構常數C2n為 5×10-14，發(fā)射孔徑 n 為8，相關系數為0.5時，誤碼率隨波長和傳輸距離的變化關系，可以看出，波長較長誤碼率相對較小，采用長波長的光進行傳輸可以有效降低系統(tǒng)誤碼率。同樣，傳輸距離到一定程度時誤碼率增加很快。

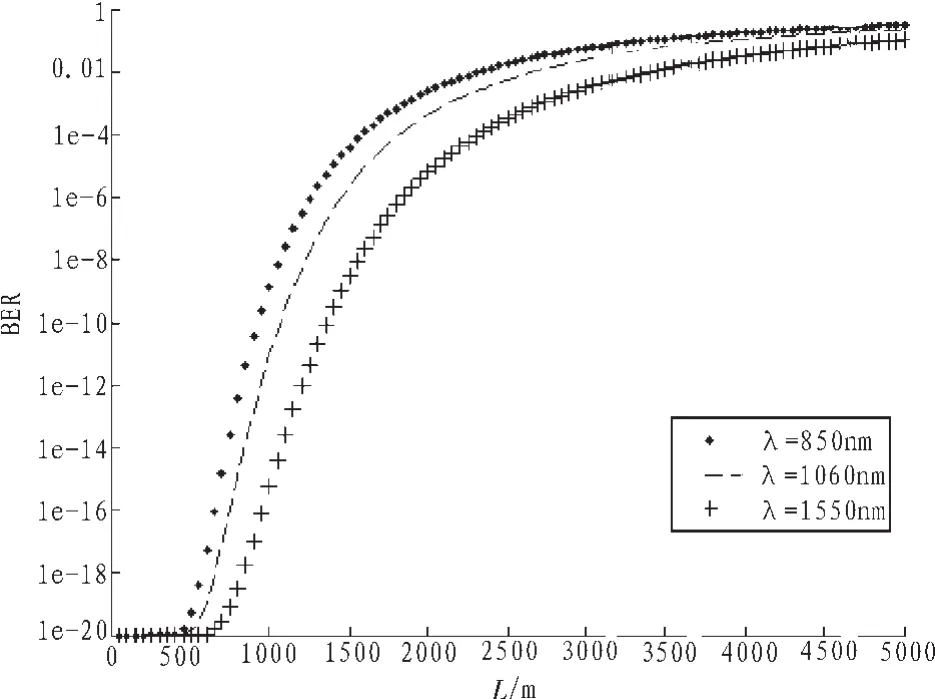
圖3 誤碼率與波長λ和傳輸距離L的關系

以上分析的都是相關系數為0.5時，誤碼率的變化。因為多孔徑發(fā)射中相關系數取值并不是一定的，下面分析相關系數對誤碼率的影響。

圖4為波長為850 nm，大氣折射率結構常數C2n為 5×10-14，發(fā)射孔徑數目 n=8，傳輸距離分別為 2、3、4、5 km 時，誤碼率隨相關系數的變化的關系圖。從圖4可以看到，相關系數越大，誤碼率就越大。傳輸距離越遠，誤碼率隨相關系數的增加也越快。

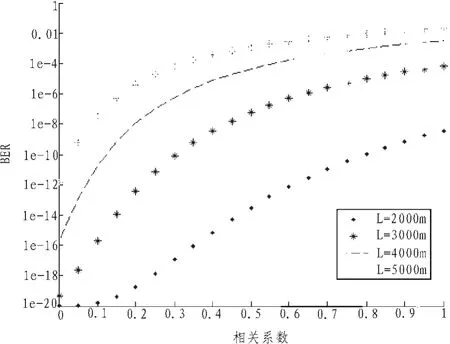
圖4 誤碼率與相關系數的關系

3 結論

在大氣激光通信系統(tǒng)中，采取多孔徑發(fā)射方式，能夠減小光強閃爍對系統(tǒng)誤碼率的影響，大大改善系統(tǒng)的通信性能。增加發(fā)射機孔徑數目，選用長波長的激光進行傳輸，都能較好的改善系統(tǒng)性能，降低誤碼率[7-8]。同時，光束間的相干系數越小，誤碼率越小。

[1]馬東堂，莊釗文.空間激光通信中的大氣閃爍問題研究[J].中國激光，2002，A29（3）：277-280.

[2]張逸新，遲澤英.光波在大氣中的傳輸與成像[M].北京：國防工業(yè)出版社，1997.

[3]Kim I I，Hakakha H，Adhikari P.Scintillation reduction using multiple transmitters[J].Proc.SPIE，1997，2990：102-113.

[4]Tatarskii V I.湍流大氣中波的傳播理論：中譯本[M].北京：科學出版社，1978.

[5]劉維慧.激光在大氣湍流中傳播時光強起伏的初步分析[D].中國學位論文全文數據庫，2004.

[6]Andrew L C，Halash M A，Hopen C Y.Theory of optical scintillation：Gaussian-beam wave model[J].Wave Random media，2001，11（2）：271-291.

[7]朱 瑞.激光多普勒流速測量技術[J].電子設計工程，2005（4）：73-74.

[8]李勇剛，白學勇，黨亞歌.基于LabVIEW的激光多譜勒信號處理系統(tǒng)[J].電子設計工程，2009，17（6）：88-89.