水泥攪拌樁重力式擋土墻變形的有限元分析

□文/趙曉萍 高 翔

基坑開挖過程中對圍護結構的變形預測與控制十分重要，有限元理論的發展為解決這一問題提供了有效途徑。本文以實際工程為背景，利用有限元理論分析水泥攪拌樁重力式擋土墻在不同開挖深度、嵌入深度及加固寬度下的變形情況，研究重力式圍護結構的變形規律。

有限元模型的計算

基本假定及建模思想

（1）模型中的介質均為連續性介質。

（2）考慮土體的非線性特點，有限元模擬中將土體本構關系定為彈塑性本構DP-model模型關系。

（3）在模擬基坑開挖過程中，將開挖部分單元用“生死單元”代替，通過“殺死”不同深度的單元來模擬土體分步開挖過程，從而了解分步開挖時間對變形及內力的影響，進而驗證“時空效應”原理的正確性。

基坑模型簡圖及有限元模型建立

工程為10棟建筑物組成的綜合服務基地，占地面積約為50 000 m2。計算的為9號樓基坑，該樓建筑面積為73 m×81 m，地上8層，地下1層用作停車庫。基坑大部分開挖深度5.4 m，局部集水坑開挖深度達到6.2 m。

由于基坑在尺寸、開挖深度、空間位置上具有對稱性，為簡化計算、加快計算速度，取基坑的1/2模型進行計算，見圖1。

根據以往工程經驗及有限元計算結果，基坑開挖影響寬度約為基坑開挖深度的3～4倍，影響深度約為基坑開挖深度的2～4倍。為了減少模型計算的“邊界的約束效應”，模型中將水平影響寬度和豎向影響深度都取為4倍的基坑開挖深度，即有限元模型的計算范圍取值為L(模型的長度)×B(模型的寬度)＝62.3 m×29.2 m。

基坑有限元模型共劃分2 536個單元和3 984個節點。位移邊界條件為兩個側面x方向的位移施加約束，y方向位移自由；上表面x、y方向位移均自由；模型底面考慮已超過影響深度范圍，可以近似認為不動，故x、y方向均施加約束。

模型參數取值

（1）土體本構關系為Dr ucker-Pr ager-model。自上而下土層的參數根據地質勘察報告進行取值，見表1。

數值模擬結果分析

不同開挖深度

為研究分步開挖過程中圍護結構體系自身及臨近土體的應力及位移變化趨勢，在有限元中通過“生死單元”技術模擬基坑分步開挖過程，本文分別選取兩種開挖深度H＝2.5 m和H＝5.4 m。

圖2為開挖深度2.5 m時的水平位移、豎向位移云圖，通過云圖的分布規律可以清楚地獲知基坑分步開挖過程中位移、應力及塑性應變的分布和變化規律。圖2中不同顏色代表不同的數值，紅色表示大值，藍色表示小值。

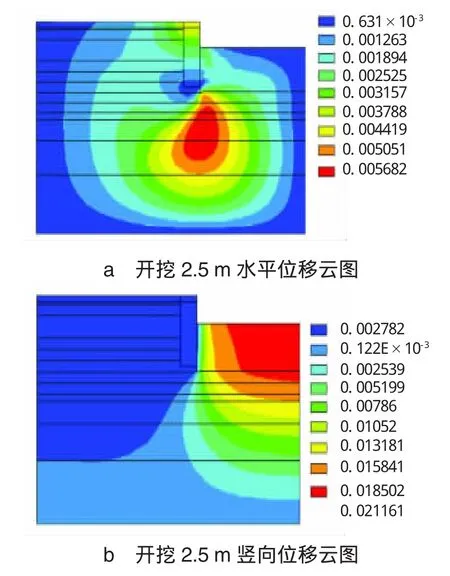
圖2 開挖深度2.5 m時的位移云圖

圖3為開挖深度分別為2.5 m和5.4 m時水泥攪拌樁重力式擋土墻水平位移曲線。

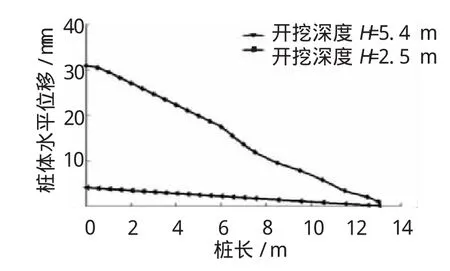
圖3 水泥土攪拌樁水平位移

從圖3可以看出，當開挖深度為2.5 m時，樁體的最大水平位移值為4.01 mm，而當開挖深度達5.4 m時，樁體最大水平位移值為30.91 mm；即當基坑開挖深度僅增加2.9 m時，樁體最大水平位移卻增加了6.7倍，增長的幅度很大。表明基坑開挖深度在時間及空間上存在一個臨界值，即當開挖深度超過某一深度之前，樁體及臨近土體的變形很小，但超過這一深度后，樁體水平位移變化相當迅速，這一過程發生的時間也比上一過程發生的時間要短。

圖4和圖5分別為不同開挖深度下臨近地表沉降曲線和坑底隆起曲線。

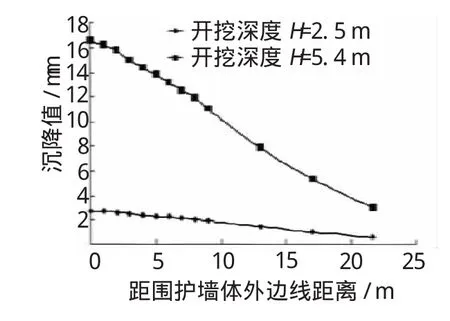
圖4 臨近地表沉降位移曲線

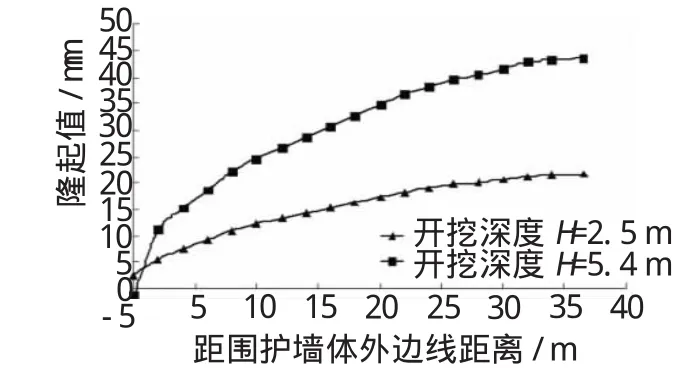
圖5 不同開挖深度下坑底隆起曲線

從圖4和圖5可以看出，曲線的變化形狀和規律均表現出在開挖的初期地表沉降及坑底隆起值較小，隨著開挖深度的增加及時間的增加，到某一臨界值后，地表沉降及坑底隆起量大幅度增加，變化非常迅速。

基坑開挖過程中樁體水平位移、臨近地表沉降及坑底隆起數值模擬結果和理論研究與眾多實測結果的變形規律和趨勢非常一致，3種變形在時間和空間分布上所具有的特殊規律很好地驗證了“時空效應”原理的存在性和正確性。

不同加固深度

為研究水泥土攪拌樁重力式擋土墻不同加固深度下圍護結構體系自身及臨近土體的應力及位移變化趨勢，選取設計樁長為13 m和16 m，同時考慮分步開挖的影響，設計開挖深度分別為H=2.5 m和H=5.4 m的情況。圖6為不同加固深度下水泥攪拌樁重力式擋土墻水平位移曲線。

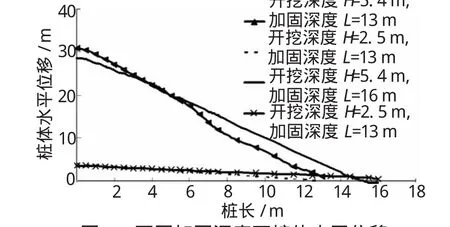
圖6 不同加固深度下樁體水平位移

從圖6可以看出，當開挖深度為2.5 m，樁長L為13 m和16 m兩種情況下樁身水平位移基本上沒有太大變化，水平位移最大值也較為接近，表明樁長增加3 m對樁身的水平位移基本上沒有影響，從另一個角度說明13 m的樁長對開挖深度僅為2.5 m的基坑不管是從圍護結構安全還是從變形角度考慮都已經是滿足要求的，繼續增加樁長并不能起到限制變形的效果，反而造成浪費；開挖深度達到5.4 m時也說明了這一現象，樁長L=16 m時的最大水平位移值僅比樁長L=13 m時的最大水平位移值小2 mm左右，增加樁長并不能很有效地抑制樁身的水平位移。

圖7和圖8分別為不同加固深度下臨近地表沉降曲線和坑底隆起曲線。

圖7 不同加固深度下臨近地表沉降

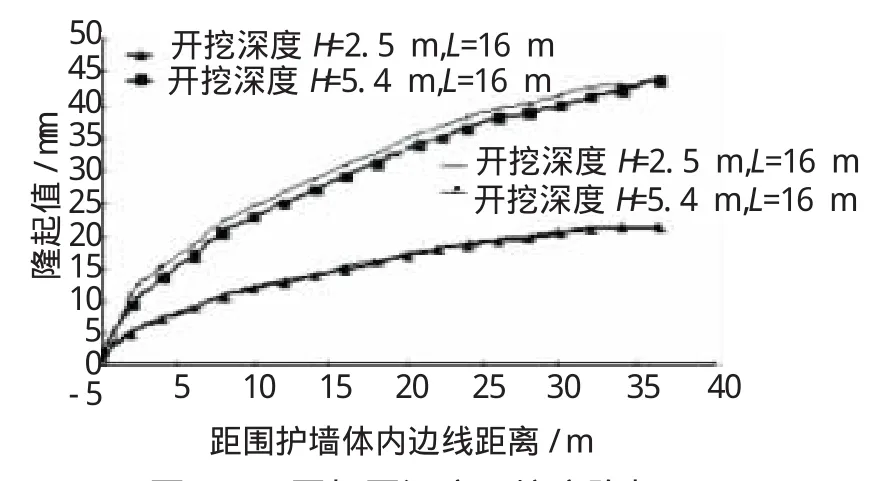
圖8 不同加固深度下坑底隆起

從圖7和圖8可以看出，在開挖深度為2.5 m時，樁長增加3 m對臨近地表沉降及坑底隆起基本沒有影響，地表沉降及坑底隆起最大值基本相同，這一變化規律與水平位移變化規律一致；當開挖深度達到5.4 m時，樁長增加3 m對臨近地表的沉降有一些影響，沉降最大值減少約4.1 mm，對坑底隆起仍然沒有太大影響，隆起最大值約增加0.8 mm。

綜上分析，欲通過增加水泥攪拌樁樁長來減少圍護結構自身的水平位移、鄰近地表沉降及坑底隆起效果不是很明顯。一般來說，水泥攪拌樁重力式擋土墻的嵌入深度為開挖深度的0.8～1.2倍，在嵌入深度滿足計算要求后，一味地增加樁長用以限制和減少變形效果不明顯，反而會造成嚴重浪費。

不同加固寬度

為研究水泥攪拌樁重力式擋土墻不同加固寬度下圍護結構體系自身及臨近土體的應力及位移變化趨勢，選取設計加固寬度為4.2 m和5.7 m，同時考慮分步開挖的影響，設計開挖深度分別為H=2.5 m和H=5.4 m的情況。圖9為不同加固深度時水泥攪拌重力式擋土墻水平位移曲線，為了與原設計加固寬度進行對比，將加固寬度為4.2 m的樁身水平位移繪制在同一張圖中。

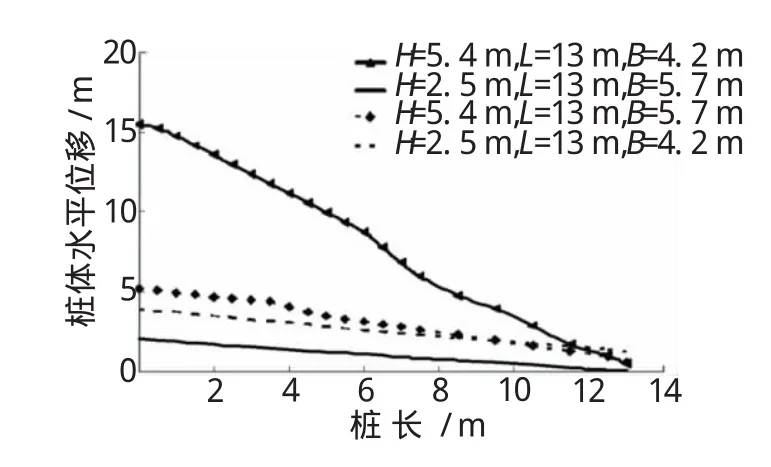
圖9 不同加固寬度下樁體水平位移

從圖9可以看出，當開挖深度為2.5 m，加固寬度為4.2 m和5.7 m兩種情況下樁身水平位移變化較大，當開挖深度為2.5 m時，加固寬度增加1.5 m后，水平位移有所減小，但減小的幅度并不是十分明顯；當開挖深度達到5.4 m時上述這一規律非常明顯；加固寬度為4.2 m時的樁頂最大水平位移值為31 mm，約為加固寬度5.7 m時樁頂最大水平位移值10.2 mm的3倍，表明加固寬度增加1.5 m對樁身的水平位移的影響非常顯著，即對樁身水平位移的限制效果非常好。從另一個角度說明盡管4.2 m厚的重力式擋土墻已經能夠滿足強度及變形的要求，但如果能夠繼續加大重力式擋土墻的加固寬度將會很高效地限制樁身水平變形的發展。

圖10和圖11分別為不同加固寬度下臨近地表沉降曲線和坑底隆起曲線，曲線的變化形狀和在時間及空間分布上的變化規律與前面的分析基本相同。

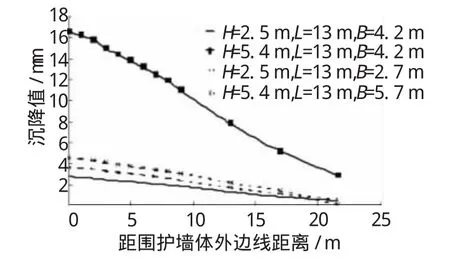
圖10 不同加固寬度下臨近地表沉降

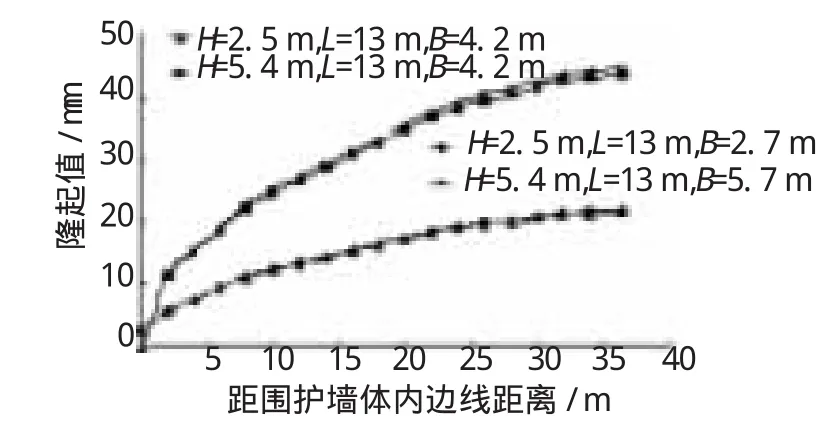
圖11 不同加固寬度下坑底隆起

從圖10和圖11可以看出，在開挖深度為2.5 m時，擋土墻加固寬度增加1.5 m對臨近地表沉降及坑底隆起有所影響，但影響不是太明顯，這一變化規律與前面水平位移變化規律基本一致；當開挖深度達到5.4 m時，擋土墻加固寬度增加1.5 m對臨近地表的沉降影響相當明顯，沉降最大值減少約11 mm，豎向沉降得到了較為顯著地限制，對坑底隆起的限制不是十分明顯，隆起最大值約增加1.5 mm。

綜上分析，欲通過增加水泥攪拌樁重力式擋土墻加固寬度來減少圍護結構自身的水平位移、鄰近地表沉降效果十分明顯。一般來說，水泥攪拌樁重力式擋土墻的加固寬度為開挖深度的0.7～0.8倍，在基坑周邊環境較為復雜的情況下，通過合適地加大加固寬度能夠較為有效地限制和減少圍護結構自身、臨近地表變形，但對坑底土體隆起變形的抑制效果不是很明顯。

結論

（1）本文通過有限元ANSYS程序建立數值模型對水泥攪拌樁重力式擋土墻圍護結構的3種變形進行了模擬并考慮了不同墻寬、墻深及分步開挖等情況下圍護結構水平變形、坑底隆起和地表沉降的變化趨勢及規律，模擬結果表明有限元模擬水泥攪拌樁重力式擋土墻的變形規律是可行、有效的。3種變形在時間和空間分布上所具有的特殊規律很好地驗證了“時空效應”原理的存在性和正確性。

（2）基坑開挖深度在時間及空間上存在一個臨界值，即當開挖深度超過某一深度之前，樁體及臨近土體的變形相當小，但超過這一深度后，樁體水平位移變化相當迅速，這一過程發生的時間也比上一過程發生的時間要短，即超過某一臨界，變形迅速完成，因此在工程實踐中，要盡量減少基坑無支撐的暴露時間。

（3）通過增加水泥攪拌樁重力式擋土墻嵌入深度，即增加樁長來減少圍護結構自身的水平位移、鄰近地表沉降及坑底隆起效果不是很明顯。

（4）通過增加水泥攪拌樁重力式擋土墻加固寬度，來減少圍護結構自身的水平位移、鄰近地表沉降效果十分明顯，但對坑底土體隆起變形的抑制效果不是很明顯。