線性函數的平均值在高中物理中的應用

臧立志

(蘇州大學附屬中學,江蘇蘇州 215006)

在中學物理中,線性函數y=kx+b或y=kx等獲得了極其廣泛的應用.利用線性函數,我們不但能正確地表達諸如由時間決定的變力,彈簧類物體的彈力,線性變化的感應電動勢,靜止液體內部的壓強,共軸轉動物體的各點的線速度等等一般的物理規律,更重要的是,我們還可以利用線性函數在定義區間 x1～x2(或 t1～t2)內的平均值ˉy=來分析和解決許多比較復雜乃至極其困難的物理問題,從而刪繁就簡,化難為易,收到良好的教學效果.下面,筆者試從3個方面展開討論.

1 關于線性變力的做功問題

這里所謂線性變力,是一種方向沿同一直線而大小隨位移均勻變化的力,亦即大小與位移成正比而方向相反的變力,其表達式為 F=-kx+b或F=-kx.反映在數學中,這種變力是位移的一次函數.對解決這種變力做功的問題,使許多初學者感到困惑不解或十分棘手.但是,從另一個角度著眼,若利用這種函數在0～x位移內的平均值即ˉF作為恒力來替代線性變力,使求線性變力做功的問題予以簡化.

例 1.如圖 1所示,把質量為 m、底面積為 S的木塊,放入密度為ρ的水內的O點,即木塊下底面在水下 h0深度處時,由于恰好受力平衡而靜止.現用力下按使其豎直向下移動 xm至 O′點,然后釋放.求木塊由O′點返回到O點時的瞬時速度.

解析:選豎直向下為 x軸的坐標正方向,以O點為坐標原點.考慮到浮力遵守阿基米德定律,可得 N=ρ gSh,其中h為木塊沒入水中的深度.從而,可得木塊所受的合力為

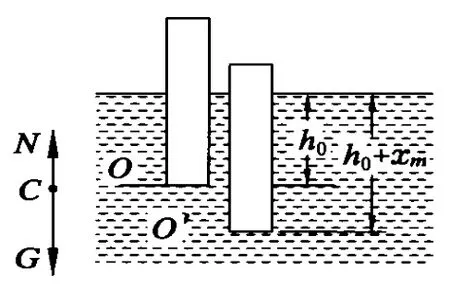
圖1

其中x為木塊在任意位置偏離O點的位移.

依題意,當木塊在O點時,

再把(2)式代入(1)式,又得 F=-ρ gSx.

由此可見,木塊在此線性變力作用下做簡諧運動.不難求出合力F在0-xm區間上的平均值為

設由O′點返回到O點時的瞬時速度為v,根據動能定理可得

最后,由(3)、(4)式即可求出

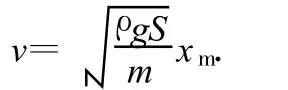
點撥:應該指出,當線性變力 F=kx與另一恒力(如此例之重力)共同作用于一個物體時,其合力也是線性的,從而形成F=kx+b形式的線性變力,其平均值的表達式與前者亦有所不同.并且這一點對于以時間為自變量的一次函數也是如此.

例2.如圖2所示,一根輕質彈簧豎直站立、下端固定在水平支持面上,恰好在彈簧的正上方高度為h的A點,有一質量為 m的物體由靜止自由下落.當物體落至彈簧上端的O點時,彈簧開始被壓縮,而當它到達B點時,物體的速度為零.試求:

(1)物體位移多大時達到最大速度,最大速度為多少.

(2)彈簧的最大壓縮量.

解析:首先,分析可知物體在豎直向下的重力、豎直向上的彈力等共同作用下,做先加速、后減速、最后靜止的變加速運動.

選豎直向下為 x軸正方向,以O點為坐標原點.由牛頓第二定律,可得

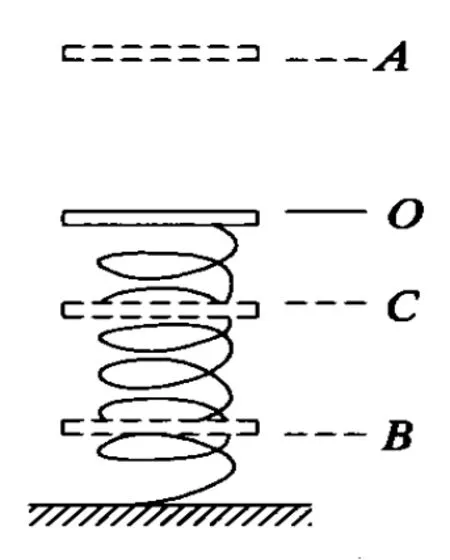
圖2

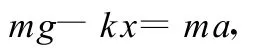
其中F=-kx為彈簧的彈力.

然后,設物體自A點下落至C點時加速度為零,此時物體達到最大速度vm;又設 OC=x1,亦即 mg-kx1=0.于是可得

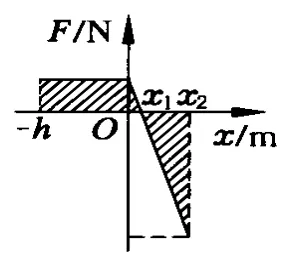
圖3

顯然,重力、彈力的合力在位移 x內的平均值為

從而由動能定理,我們不難得到

由(1)～(3)式,即可解得

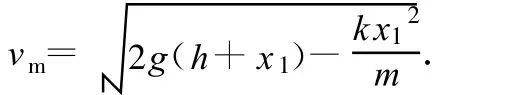
最后,依題意知物體自 A點下落到B點時速度為零,再設彈簧的最大壓縮量即OB=x2,我們由動能定理又得

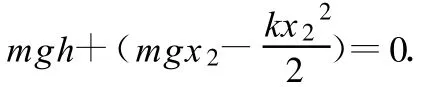
顯然,上式是關于 x2的一元二次方程.從而又可解得

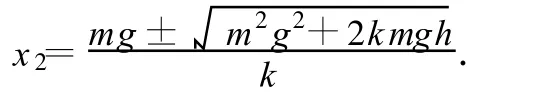
由于 m2g2+2kmgh＞m2g2,因而當根式前為“-”號時,x2＜0,舍去負解.從而可得到

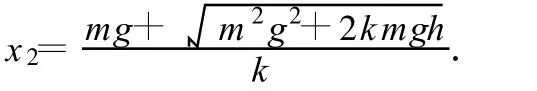
亦即線段 BC＞OC,點 C不是線段OB的中點;若 h比較大,則BC段比OC段要大得多.圖3表示出合力隨位移變化的大致情形,“陰影”的面積則為合力在相應位移內所做的功.

點撥:由此例解析可見,我們雖然先后在 AC和AB兩段位移上都利用動能定理解決問題,但由于前者與后者的位移不同,使得同一合力的平均值顯然不同;從做功角度看,造成BC＞OC的原因,顯然是在 AC一段位移上,重力做了比在BC段更多的正功.還應明確,若使上式中h=0,可知物體由O到B恰好完成簡諧運動的半個全振動,此時C點才是OB線段的中點,同時也是振動的平衡位置.

2 關于線性變力沖量的問題

這里所謂線性變力,是另一種方向沿同一直線而大小隨時間均勻變化的力,其表達式為 F=kt+b或F=kt.反映于數學中,這種線性變力是時間的一次函數.類似地,若能利用線性變力在時間0～t內的平均值,即作為恒力替代線性變力,使求變力的沖量問題得以簡化.

例3.灑水車在灑水過程中,由于水流速度、噴水口面積等在比較長的時間內,可以認為保持不變,即單位時間內流出的水的質量相等.因而,灑水車的質量是時間的一次函數,可以寫作 m=m0-kt.其中 m0為初始質量,k為質量對時間的變化率,t為灑水的時間.現設灑水車的初速度為 v0,初始質量為 m0,經過 t的時間,車速增加為 vt;再設它的牽引力F恒定不變,與路面的摩擦因數為 μ.試求:灑水車在時間t內損失的動量.

解析:首先,分析可知灑水車在水平方向的牽引力和滑動摩擦力等作用下做加速度逐漸增大的加速運動.

顯然,由于所受合力不為零,動量守恒定律不適用.但是筆者們可以先用合力的平均值求出合力的沖量,再利用動量定理即可求出動量的損失.依題意,可知其合力為

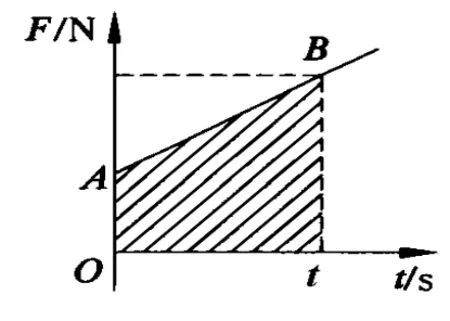
圖4

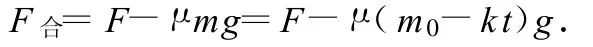
合力隨時間變化的情形如圖4中直線 AB所示,“陰影”的面積則表示了合力的沖量.在時間t內合力的平均值為

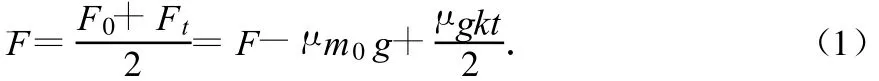
設灑水過程中損失的動量為Δp,由動量定理得

由(1)、(2)式,可以解得

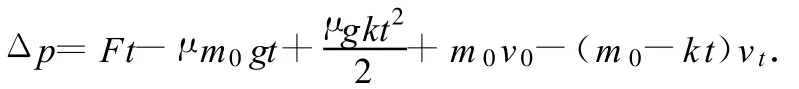
點撥:解答此題的關鍵有二:一先用線性變力——合力對時間的平均值,求出合力的沖量;進而,再利用動量定理去求動量的變化.二在全過程的動量變化之中,不但有末、初動量之差,同時必須包括流出的水帶走的動量,亦即題目所求的損失的動量.

3 線性長度導致的感應電動勢問題

電磁感應現象中也有一類隨位移或時間均勻變化的感應電動勢問題,即感應電動勢E是位移s或時間t的一次函數.類似地,筆者們也可以利用求其平均值的方法去分析和解決.

例 4.如圖 5所示,兩條平行的虛線 M、N之間存在著垂直紙面向內、磁感應強度為 B的勻強磁場.在磁場的左側另有一個位于紙面內的等腰梯形線框 ABCD,已知 AB邊的長度d,底角 α,且總電阻為 R.現使線框自左至右以速度v勻速進入磁場,自 AB邊進入直到CD邊與磁場左邊界M重合為止,所用的時間為t,那么求在此過程中通過線框某一橫截面的電量.

解析:分析可知,在題設過程中梯形線框切割部分的有效長度為

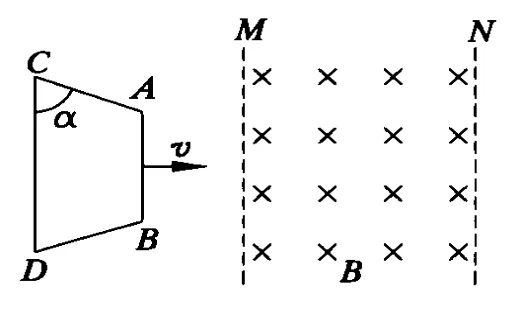
圖5

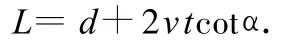
由電磁感應規律得線框中的感應電動勢

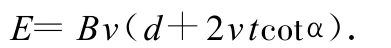
顯見,它是時間的一次函數.

然后,該電動勢在時間0～t內的平均值

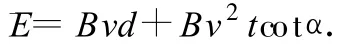
最后由歐姆定律求出通過線框某一橫截面的電荷量

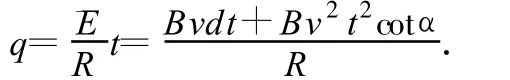
點撥:解決此題的關鍵在于,先求出線框勻速進入磁場時切割磁感線的有效長度L,再由感應電動勢的瞬時表達式求出其在時間0t內的平均值;然后,作為恒定的感應電動勢結合歐姆定律等處理.

綜上所述,若能巧妙的利用一次函數的平均值,筆者們的確可以解決中學物理中一大類物理問題.它不僅可以大幅度提高中學生分析和解決物理問題的能力、利用數學知識解決物理問題的能力,而且對于培養求異思維、巧妙思維和創新思維能力,進而大面積提高中學物理的教學質量都有十分重要的意義.

1 復旦大學、上海師范大學物理系編.物理學.上海:上海科學技術出版社,1997.

2 人民教育出版社編.全日制普通高中(必修加選修)教師教學用書.北京:人民教育出版社,2003.