構建思維平臺,促進學生思維再發展

張靜娟

(蘇州市相城區陸慕高級中學,江蘇蘇州 215131)

在高中物理的學習中,學生物理知識的獲取主要是建立在抽象思維基礎之上的概括和總結.在學生的思維活動中呈現的是經過抽象概括的物理模型和物理學規律.一個學生的抽象思維的深度和廣度是有限的,它總有一個臨界極限,這使得大部分學生在解決某些物理問題時只能徘徊于某一層面,在思維的深度和廣度上無法取得突破性進展.因此,如果我們能準確的抓住學生的思維臨界點,并采用有效的方法把它構建成一個能促使學生思維再發展的平臺,這將不僅能使學生對相關物理模型的理解得以加深、處理能力得以提高,還能促使學生思維的深度和廣度容易得到進一步的延伸和發展.

檔案保存只停留在紙質件。由于重視程度不夠，資金投入不足，檔案信息化建設的設備設施未投入，致使當前基層所檔案掃描、電子檔案等工作沒有開展。

在整個優化迭代過程中，FP設計區域的單元相對密度也在不斷發生變化。單元相對密度分布在0～1范圍之間，并以云圖形式顯示（圖4）。其中暖色系單元表示該處材料承擔著相對較高的載荷，對整體結構的剛度貢獻值較大；冷色系單元表示材料承擔的載荷相對較小，對結構的剛度貢獻值較小，該部分材料在鋼板后期重設計過程中將被移除。從整體上看，鋼板主體在橈骨遠端骨缺損層面保留了較多的材料，而在近骨折端的橈骨鋼板尺側區域（對應橈骨的中間柱區域）的大部分材料也被保留了下來。

那么,如何突破臨界點構建學生再發展的思維平臺呢?在實際教學過程中,可以從多角度引導學生構建不同問題的思維平臺.

1 從基本物理概念出發,通過拓展概念內涵和外延來構建思維平臺

物理概念是物理學的基礎.學生對物理概念理解的深度是學好物理的關鍵,但有時充分挖掘物理概念的內涵和外延,能使筆者們有如獲至寶的感覺.

在重力場中豎直平面內的圓周運動:

有了這一重力場中豎直平面內圓周運動扎實的力學知識,便可促使學生對重力場與電場的復合場中豎直平面內圓周運動的思維得到進一步發展與飛躍.

近幾年來，鉆井技術不斷進步，新技術不斷更新，尤其是各種鉆井液新型處理劑相繼問世，這就迫切要求相關行業標準能夠及時滿足技術進步的需要。但是我國目前鉆井液方面技術標準的內容和水平還不能完全適應發展的需要。在一些標準的銜接方面，還不能完全滿足與市場接軌的要求。因此就需要加大力度完善鉆井液相關標準，提高處理劑質量，推動企業間良性競爭，并滿足不斷發展的鉆井技術的需要。針對目前行業標準的現狀，制定與技術發展相適應的行業標準就顯得格外重要。

(B)電流表讀數減小,電壓表讀數增大.

(C)電流表讀數增大,電壓表讀數增大.

(D)電流表讀數減小,電壓表讀數減小.

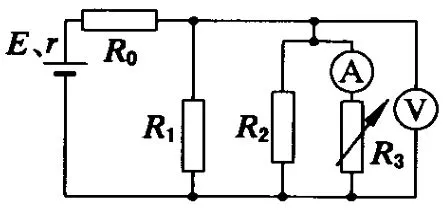
圖1

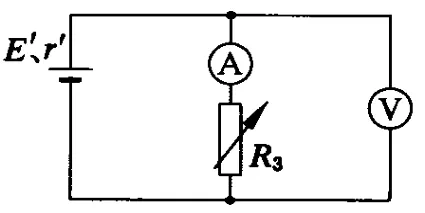
圖2

分析:學生利用上述思維平臺,不難可將圖1簡化成圖2,從而得到答案(B).

在這樣一種嚴峻的地理環境下，長期以來，民勤縣委、縣政府致力于治沙防沙，建設綠色生態文明。這次“2018首屆中國·民勤沙漠雕塑國際創作營”的呈現，便是民勤文化建設又一新的有力舉措。

當然,學生建立了這一思維平臺,還可以處理求極值問題、“測電源電動勢和內阻”實驗誤差分析等一系列問題,使學生牢固掌握這一類物理問題的解決方法,思維的深度和廣度得到再延伸和發展.

2 從物體受力特點出發,構建思維平臺

在力學中,許多問題中物體的受力情況具有一定的類似性.筆者們可以通過這些類似性引導學生構建相關問題(模型)的思維平臺,以求學生對這類問題(模型)思維的深度和廣度得到再發展.

例如:(1)如圖3,在勻加速前進的車廂內,懸掛一小球,懸線與豎直方向夾角穩定為θ,則小車加速度為 a=gtanθ.

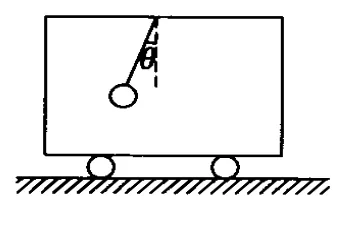
圖3

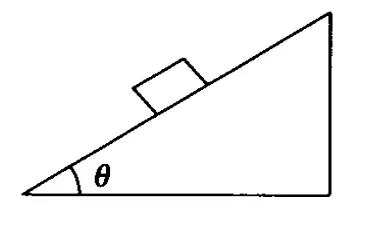
圖4

(3)如圖5,小球靜止,當 OA細繩被剪斷瞬間,小球加速度為a=gtanθ.

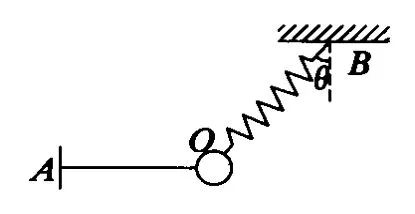
圖5

以上3題中,小物體受力特點有一定類似性,即重力、彈力和彈力與豎直方向夾角,筆者們便可構建一個如圖6受力特點的思維平臺,引導學生得到 F合=mgtanθ=ma、a=gtanθ的結論,促使學生思維得到更深更廣的發展.

例如圖7,一質量為1 kg的小球用細繩吊在傾角θ=53°的斜面頂端,斜面靜止時,球緊靠在斜面上,繩與斜面平行,不計摩擦,當斜面的 10 3 m/s2的加速度向右運動時,求繩子拉力及斜面對小球的彈力.

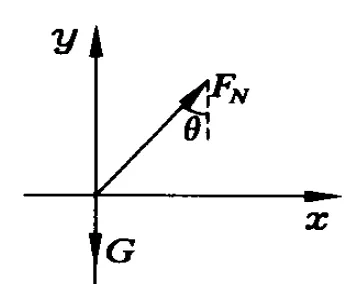
圖6

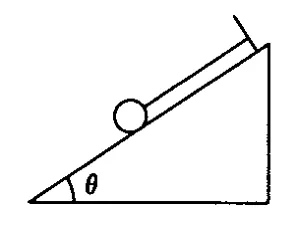
圖7

分析:學生利用上述思維平臺,不難看出當小球出現臨界情況,即小球與斜面彈力 FN=0時,a=gtan(90°-θ)=7.5 m/s2＜10 3 m/s2,由此立即能判斷小球已經飄起來,從而使學生的思維在構建的平臺上很容易得到了拓寬和延伸.

3 從物理模型的復雜程度出發,構建思維平臺

某一物理模型較為復雜,當學生難以直接接受并掌握時,我們可以根據具體情況,設法構建恰當的思維平臺,然后視情況分階段謀求思維再發展.

例如講解示波器中帶電粒子被加速電場加速后進入XX′偏轉電場,后又進 Y Y′偏轉電場,研究粒子打在熒光屏上的坐標位置和速度問題時,一般學生的空間思維能力不強.這時,可在學生完全掌握“帶電粒子在電場中的加速和偏轉”的基本物理模型后,引導他們建立如圖8所示較為簡單的思維平臺.

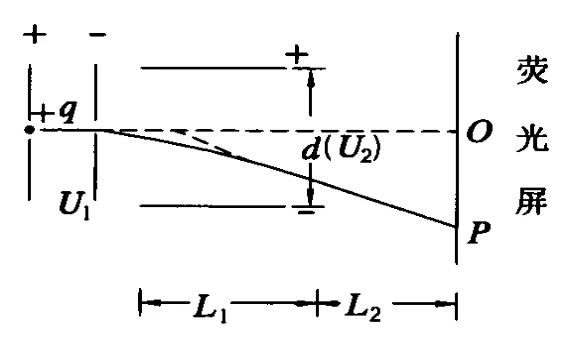
圖8

等效思想在物理學中是常用的一種思想方法,在解決某類復雜問題時,如果能引導學生構建合適的思維平臺,不但可以把復雜問題簡單化,而且有利于培養學生的發散性思維.

2.3.5 非心臟外科手術：為減少外科手術圍術期心臟并發癥風險，在術前應首先評估外科手術的緊迫性、出血風險和心血管事件的發生風險。在充分權衡出血和血栓風險的基礎上，圍手術期抗血小板治療應由多學科(外科醫師、麻醉師、心內科醫生)和患者共同決定：出血危險較低的患者，可繼續服用阿司匹林。如患者進行小型牙科手術、皮膚科操作、白內障手術等出血風險低的手術；手術相關出血風險高，應術前停用抗血小板藥物，通常術前停用P2Y12受體拮抗劑至少5d，術前需停用所有抗血小板治療的患者，如遇到血栓風險高患者，可給予靜脈抗血小板藥物GPⅡb/Ⅲa 受體拮抗劑或低分子肝素“橋接”。

(A)電流表讀數增大,電壓表讀數減小.

(2)如圖4,在一光滑斜面上,一物塊與之相對靜止,一起向前勻加速前進,則斜面體的加速度為a=gtanθ.

建立了這樣一個思維平臺,只要再適當引導學生注意運動的獨立性,便可將此物理模型的思維進一步延伸至更復雜的示波器問題(經一加速電場再先后經二個互相垂直的偏轉電場偏轉,最后打到熒光屏上的位置及速度問題).

4 從等效思想出發,構建思維平臺

即求帶電粒子由靜止開始經加速,又經U2偏轉,最終打到熒光屏上的側偏移和速度,而這一物理模型對于大部分學生是完全能夠掌握的,不難列得方程:

例如在講解帶電物體在重力場和電場的復合場中豎直平面內圓周運動時,由于勻強電場施加給帶電物體的電場力(大小、方向均不變)故可求得物體受到的重力和電場力的合力也是一個恒力,把它等效成一個新重力場內的“重力”,這樣把這類問題又轉變重力場中問題,我們應著重構建好學生重力場中豎直平面內圓周運動問題的思維平臺.

例如:在講解電源電動勢和內阻概念時,我們可以著重挖掘“電源內阻”這一物理概念的內涵和外延,引導學生構建一個把與電源串聯的定值電阻看成電源內阻的思維平臺,并引導學生的思維再發展.

以培養高素質勞動者和中初級專業人才為目標，以學生技能形成為重點，結合教材內容，建設案例庫、網絡課程、聲像資料、電子教案、數字化素材庫和虛擬仿真實訓系統等數字化教學資源；實現網上學習、在線輔導、考試評價、證書考核等功能。建立網絡交流平臺，教師上傳教學資源共享資料，學生上傳學習資料，實現教學與學習資源共享。

(1)在繩球模型中,如小球能在豎直平面內達到最高點,并持續做圓周運動,設小球在最低點a、中腰處 b(或d)、最高點 c,受到繩子的拉力大小分別為 F1、F2、F3.則F1-F3=6mg,F1-F2=F2-F3=3mg.(由動能定理和圓周運動知識可以證明)

(2)在桿球模型中,如小球能在豎直平面內到達最高點,并持續做圓周運動,設在 a、b(或 d)、c點受到桿子對它的彈力大小分別為 F1、F2、F3.則

①當小球在最高點上速率 vc≥ gl,則桿與繩一樣,桿始終提供拉力,F1、F2、F3關系同上.

②當小球在最高點速率0＜vc＜ gl,則F1+F3=6mg,且 F3＜mg(因為 c點合力指向圓心),且 F1-F2=F2+F3=3mg.

在圖 1電路中,R0、R1和 R2都是定值電阻,R3為可變電阻,當R3的阻值增大時,電流表、電壓表的讀數將如何變化?

"數據的數量、速度、種類在改變，計算機技術也在改變，而這正是讓數以萬計的商業應用成為可能的技術平臺。"

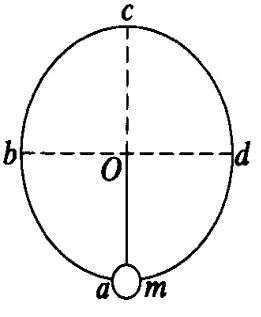
圖9

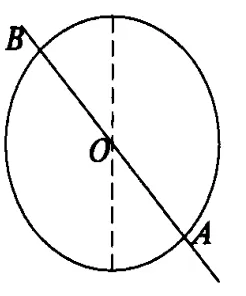
圖10

例如:半徑R=0.4 m的光滑絕緣軌道固定于豎直平面內,加上某一方向勻強電場時,帶電小球沿軌道內側做圓周運動,小球動量最大的位置在 A點,OA連線與豎直線成一角度,如圖10,在 A點小球對軌道壓力N=108 N,若小球最大動能比最小動能多14.4 J(忽略空氣阻力),求(1)小球的最小動能多大?(2)小球動能最小位置在何處?此時球對軌道的壓力多大?

分析:小球所受重力與電場力的合力是一定值,等效成一“重力”,故它的方向必與OA共線,OA連線反向延長線交軌道B點即為小球動能最小處.

《背影》是朱自清先生寫于1925年的一篇回憶性散文，講述了普通小人物的平凡小事。文章以“我”的視野記錄了1917年離開南京前往北京大學求學，父子二人車站送別的情景。在人物描寫方面本文不同于一般的抒情散文，它沒有做過多的人物神情、心理、外貌的描寫，而是細致刻畫了父親的“背影”。對于《背影》這一經典敘事性散文的研究，大致分為兩種類型：一種是從文本解讀的角度分析課文的主題、情感、人物形象等內容，《背影》隨著時代的變遷，人們對其主題的解讀也是日漸不同。另一種則是從課堂教學的角度探討教學技巧，教學方式，研究課堂實錄。本文主要研究黃厚江《背影》的課堂實錄，對他的教學語言風格做一個解析。

由動能定理得:-F合?2R=EkB-EkA,解得 F合=18 N.

學生由上述思維平臺不難得出:FA-FB=6F合,所以FB=0.

利用EDEM的后處理模塊在仿真模型中劃分統計區，統計在吸塵孔內分區的煤塵以及巖塵顆粒累積質量，進而計算出其除塵率，其中統計區內煤塵累計質量如圖4所示。

因專項資金的滯留和挪用，造成不同程度的存在獎補資金撥付不及時、專項資金掛在往來賬的問題，個別單位甚至存在財政資金公款私存現象。

由此可見,當構建了這一思維平臺,不僅能使學生快速、準確地解決重力場中豎直平面內的圓周運動問題,而且也能簡捷解決重力場與電場的復合場中豎直平面內圓周運動的絕大部分問題.

當然,構建思維平臺的角度是多方位的,關鍵是要在教學實踐中積極引導學生構建合理、科學的思維平臺,讓學生站在適合自己的思維平臺上去看所要解決的有關物理問題,問題的深度與難度都會相應變淺,更有效地幫助了學生掌握重點,逐步分解難點,以更好地適應高考物理題的靈活多變.