基于混沌振子和小波理論的軸承故障診斷方法

張 勇，紀(jì)國(guó)宜

(南京航空航天大學(xué) 振動(dòng)工程研究所，南京 210016)

混沌振子檢測(cè)微弱信號(hào)主要是利用混沌系統(tǒng)對(duì)初始條件的敏感性，當(dāng)被測(cè)信號(hào)輸入混沌系統(tǒng)后就可導(dǎo)致系統(tǒng)的動(dòng)力學(xué)行為發(fā)生變化，從而測(cè)出有用特征信號(hào)[1-2]。而小波分析是一種多尺度的分析方法，在故障診斷方面有著廣泛的應(yīng)用。現(xiàn)將小波分析思想與混沌振子結(jié)合起來(lái)檢測(cè)滾動(dòng)軸承的故障信號(hào)，以實(shí)現(xiàn)對(duì)軸承故障的成功診斷。

1 基于混沌振子檢測(cè)信號(hào)的方法

1.1 混沌振子方程

從微弱信號(hào)的檢測(cè)下限、混沌系統(tǒng)檢測(cè)信噪比、系統(tǒng)混沌判據(jù)的證明等幾方面，文獻(xiàn)[3]對(duì)Duffing方程進(jìn)行了改進(jìn)，提出的混沌檢測(cè)模型為：

(1)

式中：k為固定值,fcos (t)為周期策動(dòng)力。此方程構(gòu)成的非線性動(dòng)力系統(tǒng)是一個(gè)混沌系統(tǒng)，其參數(shù)的攝動(dòng)會(huì)引起周期解發(fā)生本質(zhì)的變化。在進(jìn)行微弱信號(hào)檢測(cè)時(shí)，將待檢信號(hào)作為周期策動(dòng)力的攝動(dòng)并入系統(tǒng),通過(guò)觀測(cè)混沌系統(tǒng)的相軌跡變化，可知待檢信號(hào)中是否含有周期微弱信號(hào)。

設(shè)待測(cè)信號(hào)為：

s(t)=Acos (t)+σrandn(t)

(2)

式中：randn(t)為滿足正態(tài)分布的均值為零的白噪聲；σ為噪聲的標(biāo)準(zhǔn)偏差；A為微弱信號(hào)的幅值。將s(t)代入(1)式得：

(3)

采用4階Runge-Kutta法，對(duì)(3)式進(jìn)行數(shù)值微分。選擇不同的步長(zhǎng)時(shí)，從同一連續(xù)系統(tǒng)中導(dǎo)出的離散系統(tǒng)也不相同，特別是在系統(tǒng)從混沌到有序轉(zhuǎn)變這一特別情況下，不同的步長(zhǎng)值將導(dǎo)致分岔值明顯不同[4]。考慮到不同的步長(zhǎng)h、頻率ω以及噪聲的強(qiáng)度都會(huì)對(duì)閾值產(chǎn)生微小的影響，經(jīng)過(guò)大量的仿真試驗(yàn)，認(rèn)為選取f=0.717較為合適，此時(shí)系統(tǒng)雖然處于混沌運(yùn)動(dòng)狀態(tài)，但即將向周期狀態(tài)轉(zhuǎn)變。

為了滿足信號(hào)檢測(cè)的需要，將(3)式進(jìn)行尺度變換：

ω2[Acosωt+σrandn (t)]

(4)

可以證明(3)式和(4)式系統(tǒng)的分岔值是相同的[5]。

1.2 混沌振子的間歇運(yùn)動(dòng)

間歇混沌主要是指非線性系統(tǒng)在時(shí)間和空間上表現(xiàn)出的有序和無(wú)序交替出現(xiàn)的特殊動(dòng)力學(xué)形態(tài)。現(xiàn)所指的間歇混沌是由周期策動(dòng)力幅值在非平衡相變臨界值附近的消漲而引起的。

當(dāng)內(nèi)驅(qū)動(dòng)信號(hào)與微弱信號(hào)存在頻率差時(shí)：

cos [(1+Δω)t+φ]

(5)

式中：fcos (t)為內(nèi)驅(qū)動(dòng)信號(hào)；Δω為微弱信號(hào)與內(nèi)驅(qū)動(dòng)信號(hào)的角頻率差；A為微弱信號(hào)幅值；φ為微弱信號(hào)的相位。對(duì)(5)式等號(hào)的右側(cè)進(jìn)行變換，如下所示：

fcos (t)+Acos [(1+Δω)t+φ]=F(t)·

cos [t+θ(t)]

(6)

其中：

(7)

(8)

當(dāng)Δω≠0時(shí)，F(xiàn)(t)在f+A和f-A之間周期性變化。這樣混沌系統(tǒng)就出現(xiàn)時(shí)而混沌，時(shí)而大周期的間歇混沌現(xiàn)象。當(dāng)Δω很小時(shí)，F(xiàn)(t)變化非常緩慢，遠(yuǎn)遠(yuǎn)慢于相變過(guò)程，因此周期和混沌的出現(xiàn)是涇渭分明的。說(shuō)明振子相變對(duì)小信號(hào)很敏感。當(dāng)系統(tǒng)存在微小角頻率差時(shí)，F(xiàn)(t)值的大小將在f值左右兩側(cè)變化，系統(tǒng)將以ΔT的周期做間歇混沌運(yùn)動(dòng)。其ΔT的值為：

ΔT=2π/Δω

(9)

因此可以通過(guò)測(cè)量ΔT的數(shù)值來(lái)獲得微弱信號(hào)頻率的數(shù)值。文獻(xiàn)[4]中應(yīng)用Duffing振子分析并得出，當(dāng)角頻率差與系統(tǒng)內(nèi)驅(qū)動(dòng)頻率之比不大于0.03時(shí)，可以觀察到間歇混沌現(xiàn)象的發(fā)生。經(jīng)試驗(yàn)發(fā)現(xiàn)，在頻差比等于0.03時(shí)，微弱信號(hào)的幅值要足夠大才能較清楚地從圖形中看出間歇混沌現(xiàn)象。而在實(shí)際中，由于微弱信號(hào)幅值都很小，通過(guò)仿真得出使用本研究所使用的振子系統(tǒng)在頻差比不大于0.02時(shí)，應(yīng)用時(shí)域圖可以較明顯地觀測(cè)出間歇混沌運(yùn)動(dòng)現(xiàn)象。(5)式中令k=0.5，f=0.717，Δω=0.01，A=0.03，φ=-π/6時(shí)，系統(tǒng)的間歇混沌運(yùn)動(dòng)的現(xiàn)象如圖1所示。

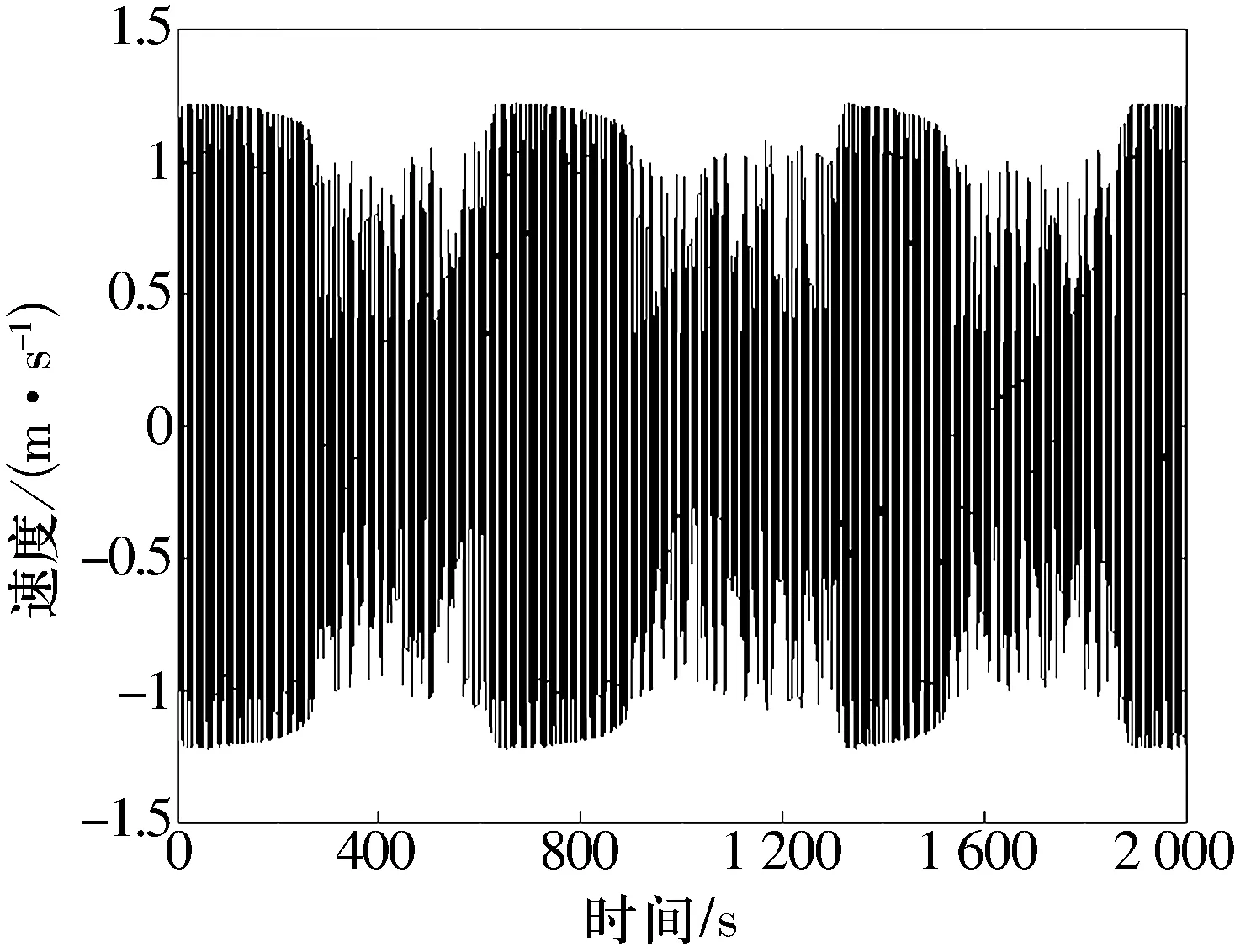
圖1 間歇混沌運(yùn)動(dòng)狀態(tài)圖

2 滾動(dòng)軸承故障分析

下面以6205軸承為例，分析其在1 797 r/min下的滾動(dòng)體故障。軸承損傷采用電火花加工而成，損傷直徑為0.711 2 mm，深度為3.810 mm，軸承故障數(shù)據(jù)的采樣頻率為12 kHz，軸承各部件的故障頻率如表1所示。

表1 軸承各部件的故障頻率

小波分析和混沌振子結(jié)合檢測(cè)滾動(dòng)軸承故障信號(hào)的基本原理如圖2所示。

圖2 檢測(cè)原理圖

滾動(dòng)體故障的原始數(shù)據(jù)時(shí)域圖如圖3所示。從表1的軸承故障數(shù)據(jù)中可以看出，其故障頻率點(diǎn)主要集中在低頻段，所以在處理數(shù)據(jù)時(shí)采用小波的多分辨率分析原理，應(yīng)用Daubechies小波對(duì)故障原始數(shù)據(jù)進(jìn)行6層分解，由于采樣頻率為12 kHz，故通過(guò)小波分解后留下94～187 Hz頻率的數(shù)據(jù)作為分析對(duì)象，其時(shí)域圖如圖4所示。再將分解后的信號(hào)輸入到混沌振子系統(tǒng)進(jìn)行頻率成分的識(shí)別。由于故障信號(hào)比較微弱(閾值為0.717)，為了便于觀測(cè)，在輸入混沌振子系統(tǒng)前可將小波處理后的故障信號(hào)適當(dāng)放大。在混沌振子系統(tǒng)的內(nèi)驅(qū)動(dòng)頻率為140 Hz和144 Hz時(shí)，得到了間歇混沌運(yùn)動(dòng)現(xiàn)象，如圖5和圖6所示。

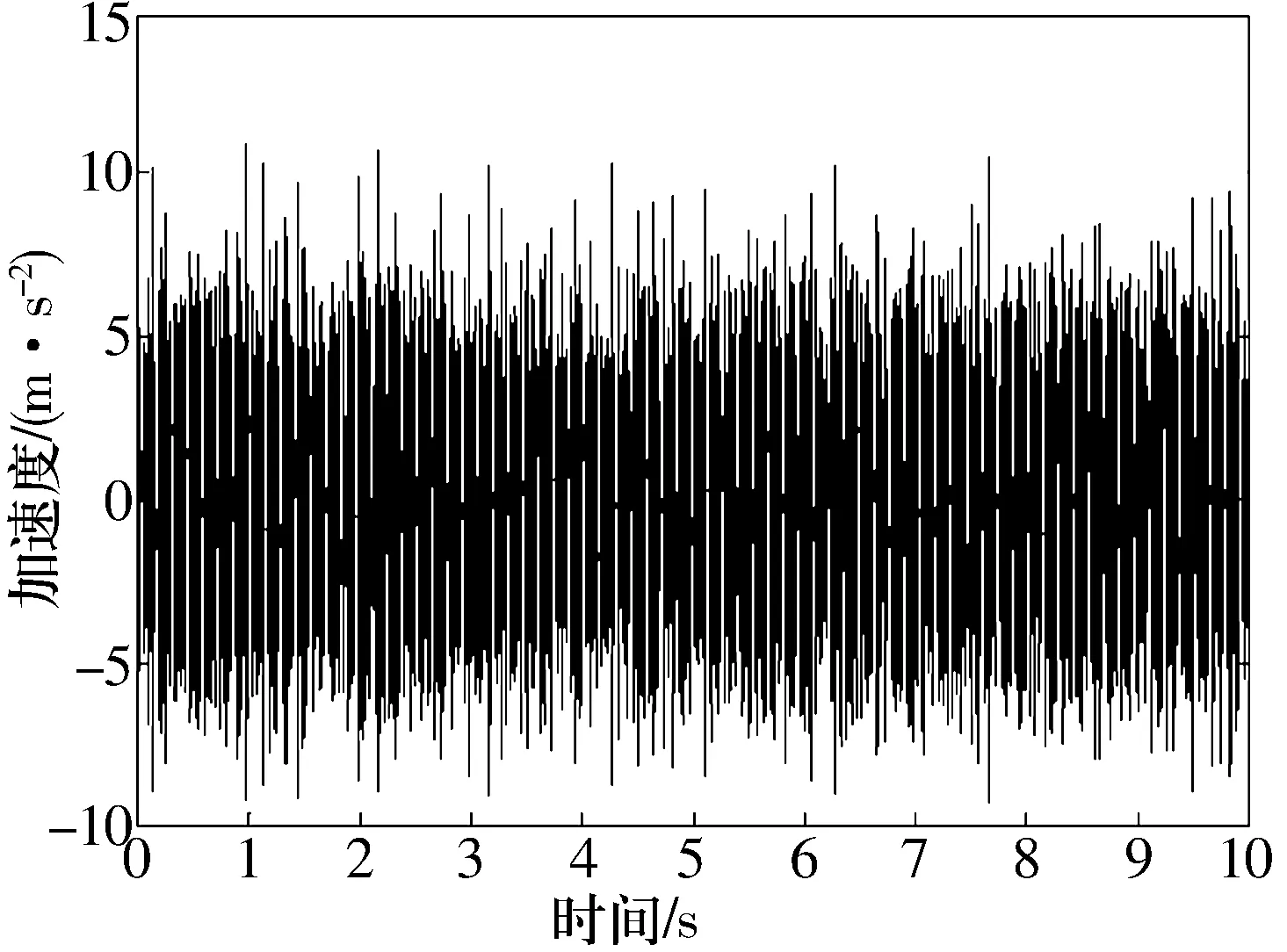
圖3 滾動(dòng)體故障的原始數(shù)據(jù)時(shí)域圖

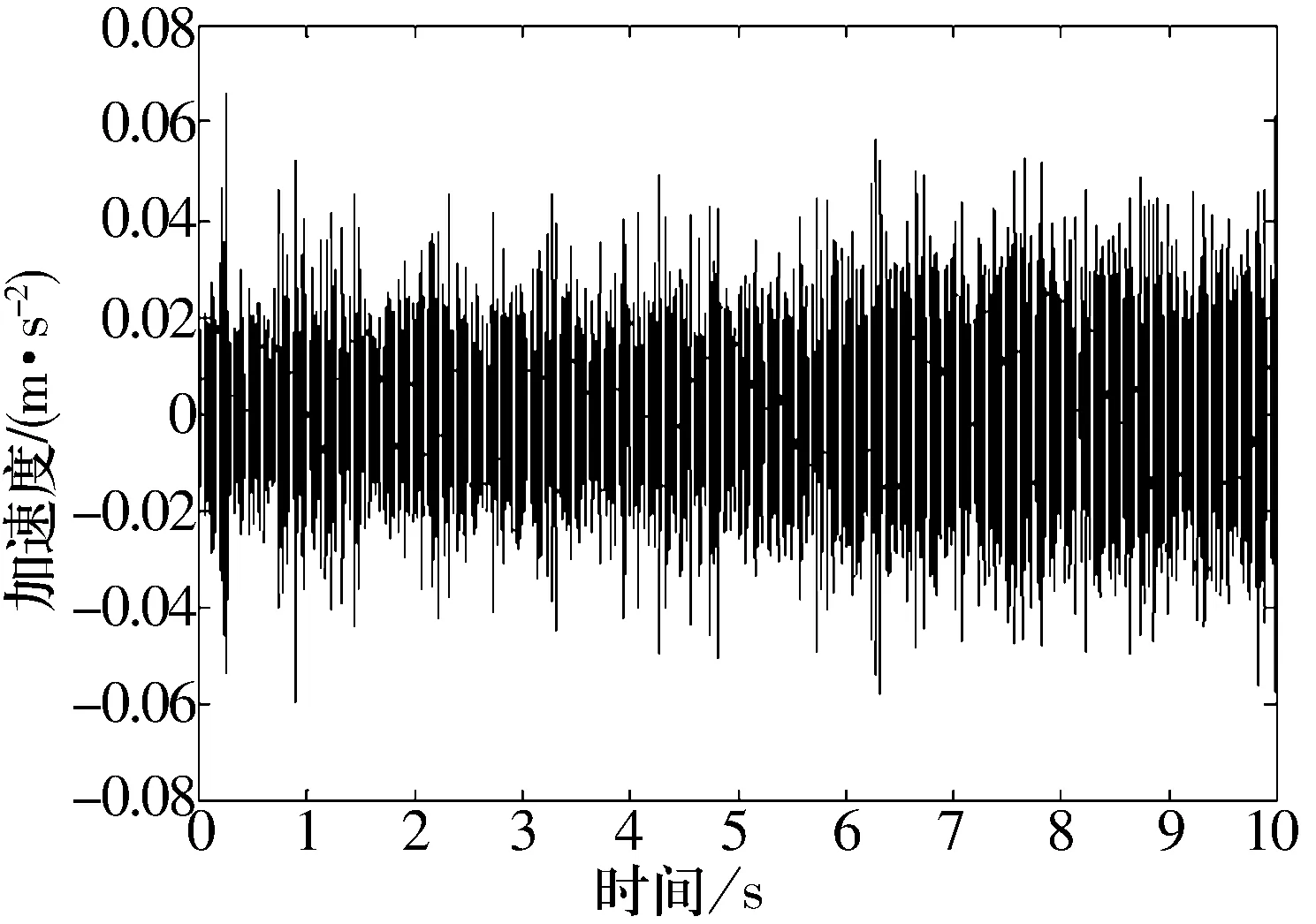
圖4 小波分解后時(shí)域圖

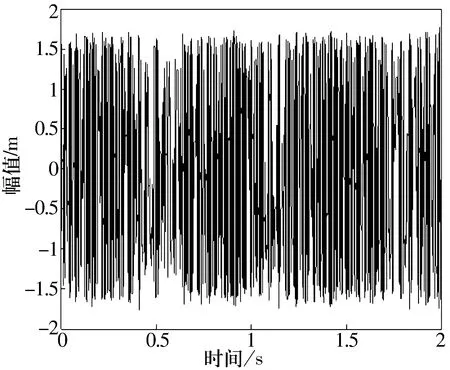
圖5 頻率140 Hz時(shí)的間歇混沌現(xiàn)象圖

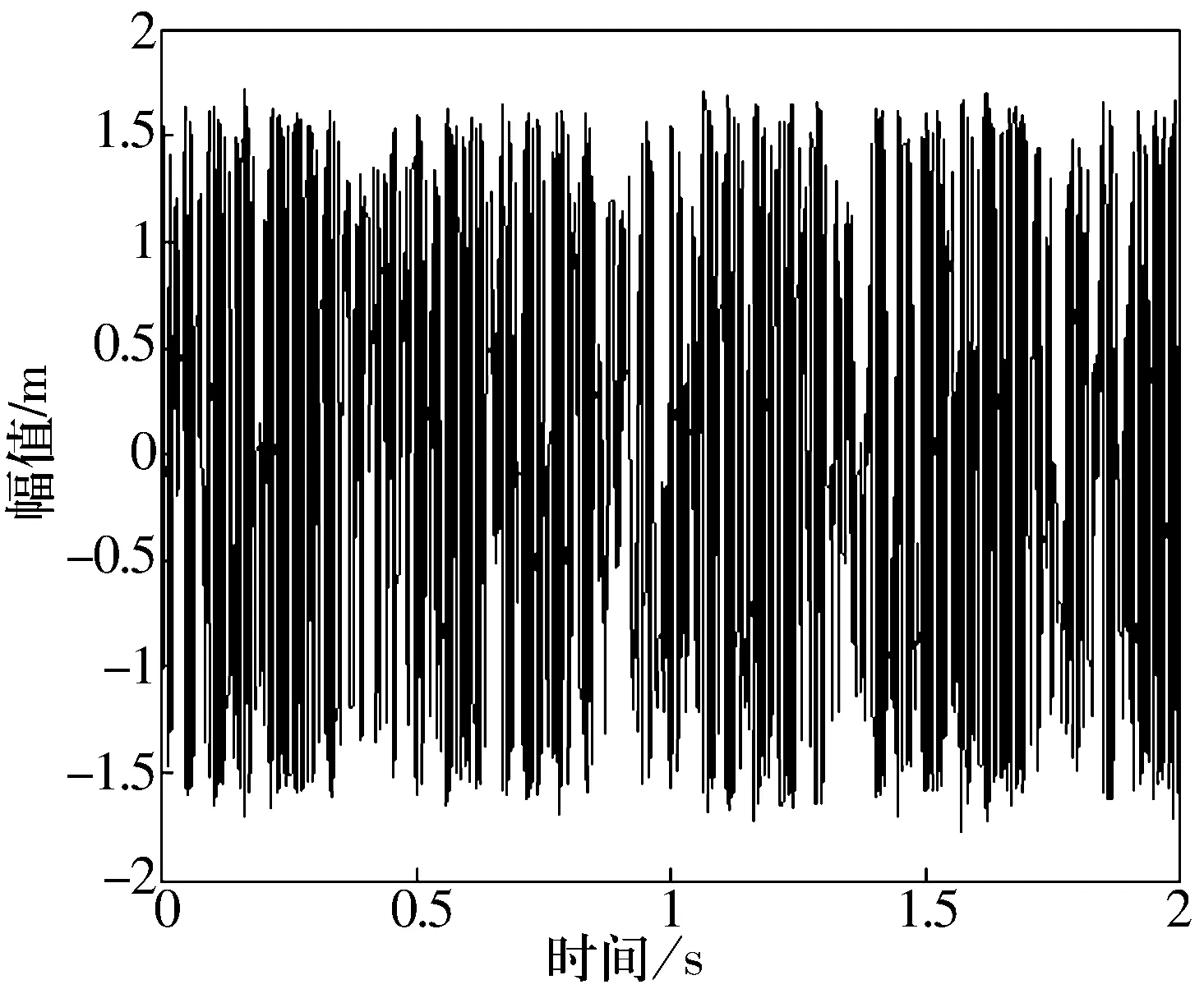
圖6 頻率144 Hz時(shí)的間歇混沌現(xiàn)象圖

在頻率為f1=140 Hz時(shí)，間歇混沌周期ΔT1=0.636 2 s，Δf1=1/ΔT1=1.572 Hz；在頻率為f2=144 Hz時(shí)，間歇混沌周期ΔT2=0.451 2 s，Δf2=1/ΔT2=2.216 Hz；通過(guò)混沌振子系統(tǒng)的間歇混沌運(yùn)動(dòng)現(xiàn)象檢測(cè)到的故障信號(hào)的頻率大小為：

與理論分析的軸承滾動(dòng)體故障頻率141.17 Hz比較接近，且誤差較小。通過(guò)以上分析可以判斷出此軸承有滾動(dòng)體故障出現(xiàn)，同時(shí)證實(shí)了所提出的方法對(duì)滾動(dòng)軸承故障識(shí)別具有一定的可行性。

3 結(jié)束語(yǔ)

介紹了利用小波分析和混沌振子相結(jié)合診斷滾動(dòng)軸承故障的一種方法,分析了其基本原理及可行性，并通過(guò)試驗(yàn)證實(shí)了其具有較高的精度和可靠性。該方法具有簡(jiǎn)單、直觀、便于實(shí)現(xiàn)的特點(diǎn)，在軸承故障診斷方面具有很好的應(yīng)用前景。