結構優化理論在預應力混凝土連續梁橋配束中的應用

王文清，侯廣偉

(1.安徽建筑工業學院，合肥 230601;2.西安鐵路局 總工程師室，西安 710054)

預應力混凝土連續梁橋以結構受力性能好、變形小、伸縮縫少、行車平順舒適、造型簡潔美觀、養護工程量小、抗震能力強及施工方法成熟等特點，在橋梁工程中得到廣泛的應用。在預應力混凝土連續梁橋的結構計算中，確定預應力鋼束(筋)的數量與位置，使結構在施工與使用階段處于合理的受力狀態是一項重要的內容。傳統的配束方法是:首先按照正常使用極限狀態的應力要求以及按承載能力極限狀態的強度要求預估預應力鋼束的數量，然后根據預應力鋼束的預估數量進行預應力鋼束的布置。由于結構的次內力與預應力鋼束的數量和布置有關，而且結構施工方法轉換體系的順序對結構次內力的影響也很大，因此預估的預應力鋼束的數量是非常粗略的，而且配置的預應力鋼束又導致內力重分配，需再調整。有時結構尺寸不符合要求，亦需要調整。此過程重復幾次，直到滿足規范要求。因此，預應力混凝土連續梁橋的配束是一項十分繁瑣的工作。

土建結構優化設計是一門土建工程與運籌學交叉的學科，它的出現使設計者從被動的分析、校核而進入主動的設計，這是結構設計上的一次飛躍。結構優化設計理論已經成功地應用于確定斜拉橋的合理成橋狀態，如彎曲能量最小法(以結構的彎曲應變能作為目標函數)、用索量最小法(以索力乘以索長累計值作為目標函數)，這些方法屬于線性規劃和非線性規劃問題。

在預應力混凝土連續梁橋設計中，在滿足連續梁橋各控制斷面應力的條件下，使預應力鋼筋數量達到最小時的配束設計方案是最經濟的。因此以鋼束用量最小為目標函數，采用優化設計方法進行預應力混凝土連續梁橋的配束設計是合理的。

1 鋼束用量最小法的基本原理和計算步驟

1.1 基本原理

在恒載、汽車荷載、溫度變化、基礎沉降等作用下，計算連續梁橋各控制截面的應力向量和其中{σ}為按照作用(或荷載)的標準值組max合得到的各控制截面最大應力向量(壓應力為正，拉應力為負，以下同)，為按照作用(或荷載)的短期組合得到的各控制截面最小應力向量，為按照作用(或荷載)的長期組合得到的各控制截面最小應力向量。

對各預應力鋼束施加單位張拉力，按施工過程求得預應力鋼束對各截面的應力的影響矩陣［C］。

根據橋涵設計規范，使用階段預應力混凝土受彎構件在正截面混凝土的壓應力和拉應力均不得超過規范規定的限值。上述限值構成了優化計算模型的約束條件。

1)混凝土壓應力限值

對全預應力混凝土構件和A類預應力混凝土構件，{σmax}+［C］{Ti}其結果均≤0.5fck(fck混凝土標準抗壓強度，Ti為第i根鋼束的張拉力)。

2)混凝土拉應力限值

當然，設計者也可根據橋梁使用耐久性的要求，提出混凝土應力(包括壓應力、拉應力、主壓應力、主拉應力等)的限制值。顯而易見，只需改變優化計算模型的約束條件，即可達到上述目的。

1.2 計算步驟

1)擬定結構尺寸和預應力鋼束的位置;

2)在恒載、活載、溫度變化、支座沉降等作用下，當不考慮混凝土收縮徐變時，按照實際施工步驟對全橋進行結構計算，形成各控制斷面的應力向量{σmax}、和

3)不考慮混凝土收縮徐變的影響，對各預應力鋼束施加單位張拉力，按施工過程求得預應力鋼束對各截面的應力的影響矩陣［C］。計算時，考慮了除混凝土收縮徐變影響以外的全部預應力損失;

4)求解U→min的線性規劃問題，得到不考慮混凝土收縮徐變時的鋼束張拉力 { T0};

5)將索力轉換成相應的鋼束數目，將此結果帶入到計算模型中重新進行計算，并考慮混凝土收縮、徐變的影響，重新形成各控制斷面的應力向量 { σmax}、此時，預應力鋼束考慮了包括混凝土收縮徐變影響的全部預應力損失;

6)重新求解 U→min的線性規劃問題，得到考慮混凝土收縮徐變的鋼束張拉力 { T1};

7)對連續梁橋的各控制斷面進行應力驗算;

8)重復第5)～7)步，直到整個結構滿足應力條件為止。在一般情況下，2～3個循環即可達到設計要求。

2 算例

某三跨變截面預應力混凝土連續梁橋，跨徑組合為(40+60+40)m，支點梁高3.3 m，跨中梁高1.6 m，如圖1所示。上部結構采用雙幅橋布置，主梁采用單箱雙室的箱形截面，箱梁的頂板寬13.5 m，底板寬8.5 m，頂板厚22 cm，腹板厚30 cm，底板厚40～25 cm，如圖2所示。箱梁采用 C50混凝土，預應力鋼材采用ASTM A416-87a標準270級鋼絞線，公稱直徑為15.24 mm，抗拉強度標準值為1 860 MPa。設計荷載為公路—Ⅰ級。主梁按照全預應力混凝土結構進行設計。本橋采用懸臂掛籃法施工。

圖1 橋梁立面與截面編號(單位:cm)

圖2 橋梁橫斷面(單位:cm)

預應力鋼束的布置形式，與橋梁結構體系、受力情況、構造形式和施工方法都有密切關系。采用懸臂掛籃法施工的預應力混凝土連續梁橋的布束形式分為懸臂力筋、中跨力筋、邊跨力筋和連續力筋。布置在梁頂的懸臂力筋主要承受結構的重量與施工荷載，中跨合龍段附近的下緣鋼束和邊跨用支架施工端部梁段的下緣鋼束除了承受活載需要外，常因結構次內力在這些部位產生正彎矩而需要布置。根據以上的布束特點，擬定本橋的預應力鋼束的位置，如圖3～圖5所示。

圖3 懸臂鋼束布置(單位:cm)

圖4 中跨鋼束布置(單位:cm)

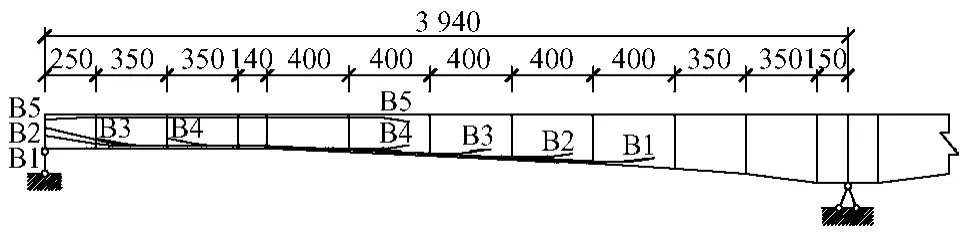
圖5 邊跨鋼束布置(單位:cm)

對各預應力鋼束施加單位張拉力，按施工過程計算預應力鋼束對各截面的應力的影響矩陣，見表2。求解U→min的線性規劃問題，得到不考慮混凝土收縮徐變時的鋼束張拉力，并將索力轉換成相應的鋼絞線數量。這時得到的各個鋼束數量是不均勻的，需要對鋼束數量進行均勻化處理。鋼束數量的均勻化處理是通過指定優化模型中的設計變量(鋼束數量)的值實現的。鋼束均勻化順序為:懸臂鋼束→邊跨鋼束→中跨鋼束。當懸臂鋼束數量調整以后，邊跨鋼束和中跨鋼束的數量隨之發生變化。當邊跨鋼束數量調整以后，中跨鋼束的數量隨之發生變化，從而實現了鋼束的自動調整，避免了傳統方法中的顧此失彼的現象，見表3。

表1 各控制截面的應力MPa

表2 預應力鋼束施加單位張拉力時截面的應力 Pa/kN

將均勻化后的優化結果帶入到計算模型中重新進行計算，當不考慮混凝土收縮徐變時，在恒載、汽車荷載、溫度變化、基礎沉降等的作用下主梁應力如圖6所示。當考慮混凝土收縮徐變時，由于混凝土收縮徐變產生的次內力以及預應力鋼束由于混凝土收縮徐變引起的預應力損失的影響，局部的主梁應力不滿足規范要求，如圖7所示。

圖6 不考慮混凝土收縮徐變時的主梁最小應力(單位:MPa)

圖7 考慮混凝土收縮徐變時的主梁最小應力(單位:MPa)

以上述計算結果為初始狀態，并考慮混凝土收縮徐變的影響，重新形成各控制斷面的應力向量以及預應力鋼束對各截面的應力的影響矩陣，再次求解線性規劃問題，并對各鋼束數量進行均勻化處理。最終的各預應力束的鋼絞線數量見表4。在各種作用或荷載的作用下，主梁應力滿足規范設計要求，如圖8、圖9所示。

圖8 在作用的短期效應組合下主梁的最小應力(單位:MPa)

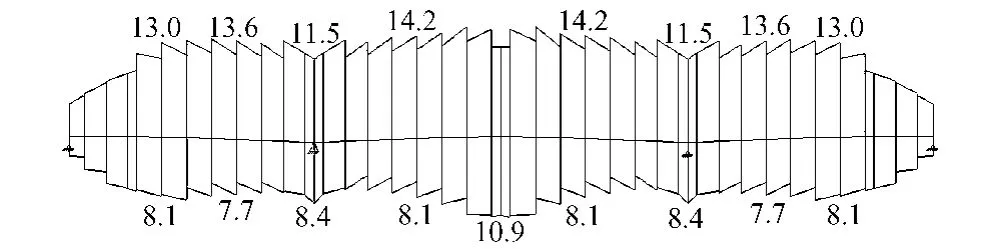
圖9 在作用的標準值組合下主梁的最大應力(單位:MPa)

表4 預應力鋼束數量表

4 結語

基于預應力混凝土連續梁橋的配束設計的傳統方法，參考確定斜拉橋合理成橋索力的“用索量最小法”，把結構優化設計理論應用于預應力混凝土連續梁橋的配束設計。通過改變優化模型的限制條件，設計者可靈活地控制混凝土的應力，并且實現鋼束的自動調整，不會發生傳統方法中的顧此失彼現象，而且可得出比較經濟的配束結果，具有廣闊的應用前景。

[1] 徐岳，王亞君，萬振江.預應力混凝土連續梁橋設計［M］.北京:人民交通出版社，2000.

[2] 范立礎.橋梁工程(上冊)［M］.北京:人民交通出版社，2001.

[3] 范立礎.預應力混凝土連續梁［M］.北京:人民交通出版社，1988.

[4] 項海帆.高等橋梁結構理論［M］.北京:人民交通出版社，2001.

[5] 賀栓海.橋梁結構理論與計算方法［M］.北京:人民交通出版社，2003.

[6] 張炳華，侯昶.土建結構優化設計［M］.上海:同濟大學出版社，1998.

[7] 江愛川.結構優化設計［M］.北京:清華大學出版社，1986.[8] 中華人民共和國交通部.JTG D62—2004 公路鋼筋混凝土及預應力混凝土橋涵設計規范［S］.北京:人民交通出版社，2004.