鐵路路基沉降評估中預測模型的選擇

劉俊飛，趙國堂，2

(1.西南交通大學 巖土工程系，成都 610031;2.京滬高速鐵路股份有限公司，北京 100038)

新建鐵路線下工程沉降評估是針對無砟軌道鋪設條件的評估，是通過對線下結構既有沉降觀測數據的分析，預測其遠期沉降，來判斷和檢驗能夠滿足工后沉降要求的無砟軌道鋪設時機。沉降評估是解決當前設計階段沉降計算精度不足與無砟軌道線路毫米級工后沉降控制標準之間矛盾的必要途徑。隨著線下工程施工中和施工后持續的沉降觀測，及時進行沉降評估，動態地驗證或調整后續施工的時間節點和設計措施，進行信息化施工，是實現新建鐵路沉降控制標準的關鍵手段。這種方法正符合了劉建航院士總結的巖土工程工作方法的十六字訣:“理論導向，實測定量，經驗判斷，檢驗驗證”[1]。新建鐵路設計階段的沉降計算起著“理論導向”和“經驗判斷”的作用，而沉降觀測與評估則是“實測定量”和“檢驗驗證”。

路基、橋梁等線下工程必需在沉降評估通過后，方可開展無砟軌道鋪設施工。相對于橋梁等工程，路基沉降量一般較大，沉降穩定所需時間一般較長，所以路基的沉降評估顯得更為重要。

《客運專線鐵路無砟軌道鋪設條件評估技術指南》(以下簡稱《指南》)規定:路基沉降根據填筑完成或堆載預壓后不少于3個月的實際觀測數據作多種曲線的回歸分析，進行沉降預測[2]。其條文說明中給出了雙曲線法、三點法、拋物線法、指數曲線法、沉降速率法、星野法、Asaoka法、泊松曲線法、灰色理論和人工神經網絡等分析方法。此外，還有學者提出一些新的預測方法[5]。

面對這些多種沉降預測方法，如何判斷它們的適用性和沉降預測結果的有效性，選擇恰當的預測模型是沉降評估工作的關鍵之一。本文將結合新建鐵路線下工程沉降評估中沉降預測的特殊性，對這些預測模型的適用性進行初步分析，并提出預測模型的優選方法。

1 新建鐵路路基沉降預測的特殊性

新建鐵路路基沉降的預測并非一個完全的“黑箱系統”，只根據現場反饋的數據本身進行推算，它必需考慮到沉降評估工作本身的特殊性。路基沉降預測數學模型的確定需要通過模型實際意義的檢驗，新建鐵路路基沉降預測的特殊性主要表現為以下三點:

1)要求數學模型具備連續性和單調性

恒載作用下沉降量是連續的，并隨時間的增加而增加。用數學函數S(t)表示t時刻沉降，則該函數對時間 t求導應 >0，即

若用負數表示沉降值，則式(1)中不等式符號為≤。

2)對遠期沉降的預測，要求數學模型具備有界性

恒載作用下沉降速率隨著時間的增加不斷減小，并趨于穩定。另一方面，沉降評估針對的是工后沉降，這就要求預測出t→∞時的沉降，至少是無砟軌道主體設計年限內(一般不小于60年)的最終沉降量。這就要求沉降預測的數學模型本身能夠求取極限，即

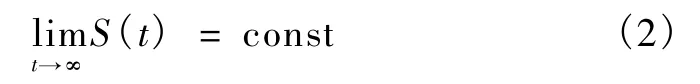
其它巖土工程中的沉降預測多為短期預測。例如，建筑基坑工程中通過坑壁附近的沉降觀測對基坑側壁的穩定性進行判斷，軟土路基填筑工程通過原地面或路基表面的沉降觀測對路堤邊坡的穩定性進行判斷，只需要對一天或數天之內的沉降進行短期預測。在高速公路工程中，也有對工后沉降的預測，其預測時間一般結合道路路面的使用年限，設為15年或20年。

3)對預測的可靠性要求較高

為了保證新建鐵路線路的高平順性和高可靠性，無砟軌道的工后沉降標準十分嚴格。我國高速公路工后沉降控制標準要求僅為一般路段不大于30 cm，橋頭不大于10 cm，與我國普速鐵路標準相當。而我國《新建時速300～350 km客運專線鐵路設計暫行規定》要求無砟軌道地段路基工后沉降一般不應超過扣件的允許調高量15 mm，并有其它嚴格的縱向差異沉降的限值要求。

新建鐵路除對工后沉降嚴格要求外，也同時需要在沉降評估中的沉降預測具有較高的可靠性。

2 《指南》中各沉降預測模型分析

《指南》中列出的十余種沉降預測方法可分為兩大類:曲線回歸分析法和系統科學法。其中，曲線回歸分析法都有一定的顯式數學表達式，系統科學法則不采用顯式數學表達式，而是采用某種系統科學理論對數據進行處理和分析。《指南》中的系統科學法包含灰色理論和神經網絡兩種。這兩種方法都是近些年發展并興起的新的數學方法。

《指南》明確規定了路基沉降觀測的頻次，指出回歸分析的時間不早于恒載期3個月，并在此基礎上提出了檢驗沉降預測有效性和可靠性的三個標準:①相關系數標準。曲線回歸的相關系數不低于0.92。②沉降速率標準。間隔不少于3個月的兩次預測最終沉降的差值不大于8 mm。③完成的沉降量標準。路基填筑完成或堆載預壓完成后已產生的沉降占預測最終沉降的比例不小于75%[2]。

這三個標準中，相關系數標準僅適用于回歸分析方法，而另外兩個標準則只是經驗性的控制方法。可見，《指南》在預測模型的選擇上給了評估人較大的自主空間，需要評估人在多種預測模型之間進行橫向比較，進一步優選出適當的預測模型。

因此，有必要首先對《指南》中各種預測模型進行一下總體上的對比和分析。各模型對數據的要求和理論依據的對比見表1。

2.1 系統科學法預測模型分析

1)灰色理論

灰色系統的任務是少數數據建模，目標是微分方程建模，要求動態信息的開發、利用和加工，充分開發利用少數數據中的顯信息和隱信息。一般來說，微分方程只適合連續可導函數，而灰色系統的行為特征是用時間序列表征，是一種離散的函數。為建立微分方程模型，灰色系統理論通過關聯分析，提取建模所需變量，并在對離散函數的性質進行研究的基礎上，實現對離散數據建立微分方程的動態模型，即灰色模型(Gray Model，簡稱 GM)。

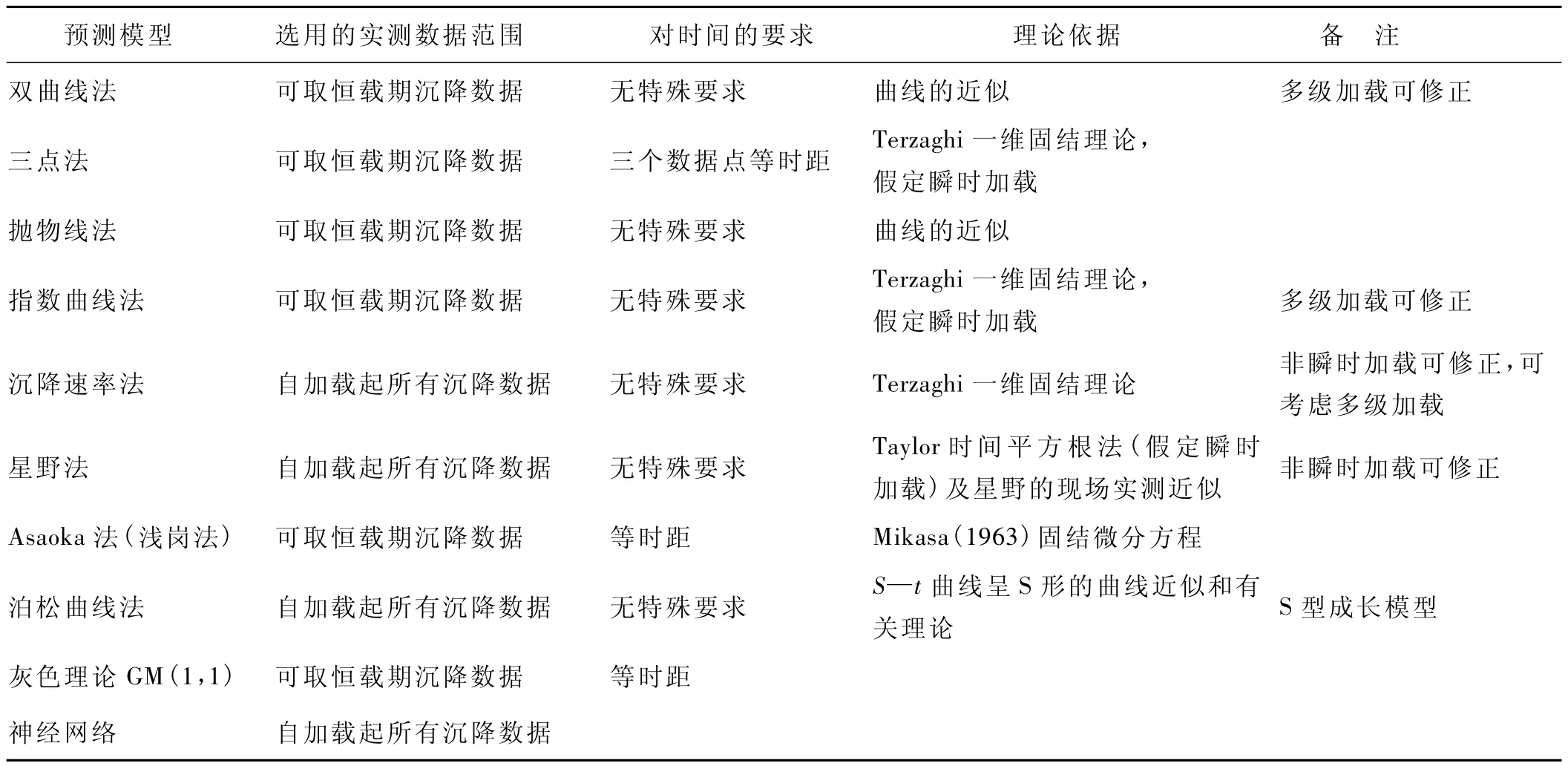
表1 《指南》中各沉降預測模型對數據的要求和理論依據

一般的灰色模型為GM(h，n)模型，表示h個變量的n階微分方程。在巖土工程有關變形問題的預測研究中，目前用得最多的是 GM(1，1)模型，因為變量越多，階數越高，計算量就越大，且精度也不一定就很高。GM(1，1)要求數據等時距，因此需要預先對既有沉降數據進行等時距處理，如采用樣條曲線上內插的方法獲得等時距沉降數據。

由于灰色模型是通過離散函數對時序數據的加工和處理，它并不具備有極限的特征。圖1為對某組沉降數據的GM(1，1)預測，可以發現其后期預測值并沒有收斂的趨勢，沉降反而有所加速，這與地基沉降的自身特征明顯不符。雖然該組數據并不滿足恒載期不少于3個月要求，但是GM(1，1)對遠期沉降預測的不適應性已暴露無遺。可見，GM(1，1)僅在短期沉降預測中可以使用。

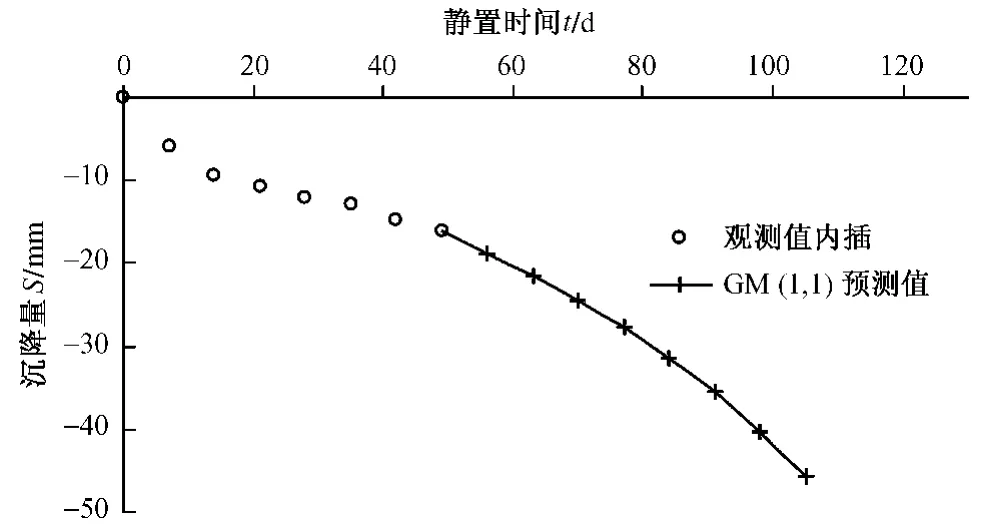
圖1 GM(1，1)沉降預測示例

2)神經網絡

神經網絡不需要精確的數學模型，運用由輸入層、隱層和輸出層組成的神經網絡的非線性映射能力，對實測數據進行直接建模，常用的算法有BP算法等。

模仿人腦的學習過程，神經網絡預測路基沉降時序問題，需要學習訓練和預測兩個過程。神經網絡能夠把地基處理方式、地基土模量與厚度、填土高度等因素納入“學習”范圍，通過數學上的“學習訓練”使輸出接近實際值。

通過神經網絡的學習訓練后，當輸入值為接近其學習范圍時，能夠獲得較為理想的效果。然而，在沉降評估階段無法獲得實測的遠期沉降數據，就世界范圍來看，高速鐵路也仍是一個新生事物，其它高速鐵路的歷史性數據也無法獲得，因此神經網絡對遠期沉降的“學習”也無從談起。這就限制了當前的新建鐵路地基沉降神經網絡的預測，即僅適用于短期預測。

2.2 曲線回歸分析法預測模型分析

回歸分析是數理統計學的重要分支，其應用范圍十分廣泛。回歸模型的數學形式可以基于一定的理論推導，也可以根據曲線的近似。由于當前的巖土工程理論和技術水平，并不能通過理論推導來獲得準確的S(t)數學模型，因此即使表1中所列的基于一定固結理論的回歸分析法模型中的數學形式也只能是近似，仍需要根據實測數據進行回歸分析。

《指南》中各回歸分析法預測模型都能滿足式(1)所表示的連續性和單調性要求。考察各回歸分析法預測模型的有界性則發現，除拋物線法外，其它幾種回歸模型都可以求得極限。

拋物線法來自于文獻[10] ，其沉降曲線的一般表達式為

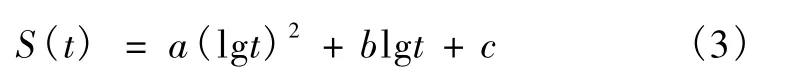
式中，a、b、c為待定常數。其極限無法求得，該函數為發散函數。

究其原因，該方法所列的表達式只適用于對固結曲線前段的擬合，不能將式(3)擴展到 t較大的情況。該文獻作者指出，最終沉降量近似等于常數項c。這一結論也緣于經驗性的判斷，在使用該模型時應予以注意。若沉降評估者無相應經驗，不建議使用本模型。

幾種回歸分析法模型中，三點法與指數曲線法的理論依據完全相同，它們的區別僅在于求解方法的不同:三點法利用三點的數據解方程組(三和值法)求取各參數，而指數曲線法可采用非線性最小二乘獲得估計值。在正態誤差假定下，非線性最小二乘估計值比三和值更精確[4]。

另外，需要說明的是泊松曲線法，它是一種S型曲線模型。S型曲線模型又稱“成長模型”，它表示地基沉降從加載伊始經歷了一個“成長—發展—穩定”的過程，沉降曲線呈S形。文獻[9] 從理論上證明了線性加載或近似線性加載情況下，沉降—時間曲線呈S形。實踐表明，S型沉降曲線多出現于加載過程較慢的軟土路基。因此S型成長模型所統計的數據范圍包含自加載起所有的沉降數據，而其它回歸分析方法常用于恒載期的數據統計。

新建鐵路出于沉降控制的需要，在軟弱土地基路段均進行了良好的地基處理，路堤填土施工也一般較快，S型沉降曲線并不多見。

3 用殘差分析輔助判斷預測結果的可靠性

《指南》中用相關系數作為沉降預測可靠性的數學標準。非線性回歸的相關系數是比照線性回歸中相關系數的方法，采用下式求得

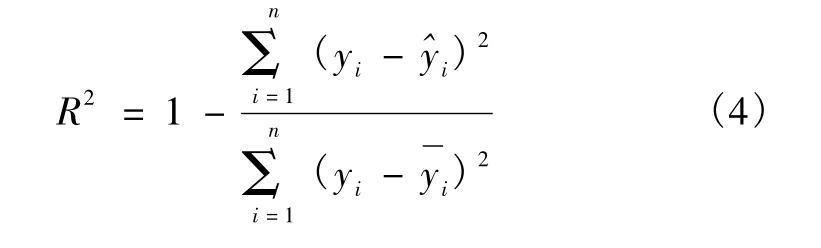
式中，yi為第i個觀測值，為回歸擬合值，為觀測值的平均值，稱為殘差，記為ei。

文獻[4] 指出，對非線性強度很高的回歸方程在使用相關指數R2時應慎重。1990年就有人提出 R2不能用于非線性回歸方程的評價，目前這一問題的研究已引起一些學者的關注。一般地說，當非線性回歸模型選擇正確，回歸擬合效果較好時，相關指數R2能夠如實反映回歸擬合效果;而當回歸擬合效果較差時，相關指數R2則不能夠如實反映回歸擬合效果，甚至可能取為負值。

另一方面，對基于數據統計的預測而言，建立回歸方程時樣本容量越大，預測的精度就越高;預測時所給定的t越靠近樣本t的平均值，預測的精度越高。這就要求沉降觀測應保證應有的頻次，沉降評估時選擇的統計數據范圍應盡量大，同時要求沉降評估的時間不能太早。

實際工程，沉降觀測的頻次可以保證需要，沉降觀測數據的質量也可以通過技術手段得到保障，這樣時間便成為控制沉降預測可靠性的一個關鍵因素。施工中，軌道板鋪設和線上工程各專業施工等大量后續工作需要在沉降評估通過后進行，路基的靜置時間過長是客觀條件所不允許的。因此需要評估者盡早根據既有數據做出可靠的沉降預測。

下面以新建鐵路李窯試驗段A區為例，通過對該點沉降曲線擬合特征的分析，研究提高沉降預測可靠性的方法。

李窯試驗段A區為濱海相沉積的深厚軟弱土地基，采用樁網復合地基加固，樁長24 m。路堤設計填高6.9 m，堆載預壓高度3.5 m。該處路基已完成填筑、靜置、預壓土卸載階段，沉降觀測歷時較長，具有一定代表性。該區自填筑施工開始，第16 d完成路堤和堆載預壓土填筑，第278 d卸除預壓土，第288 d完成預壓土卸載。路基中心CFG樁頂沉降觀測數據見表2。

從《指南》所列的幾種回歸分析模型中選取具有代表性的雙曲線法、指數曲線法和星野法三種模型分別進行回歸分析，曲線擬合結果見圖2。雙曲線法、指數曲線法和星野法預測得到的最終沉降分別為－48.7 mm、－43.4 mm和 －50.2 mm，其相關指數 R2分別為0.985 9、0.987 1和0.969 4。

由圖2可以看出，三種曲線具有不同的曲率適應性。其中，指數曲線收斂速度較快。雖然指數曲線法的相關指數最高，但可以看出它的預測值偏小，并不是最可靠的結果。三種擬合方法的殘差分布見圖3。從圖3可見，三種擬合的殘差分布都不完全具備正態特征，特別是尾段殘差仍有較為明顯的增大或減小。這種現象表現了天然土體性質和地基沉降過程的復雜性，所用的函數還不能完全反映沉降發展的規律。另一方面，也可以利用這一現象對長期預測的傾向性進行判斷，以提高預測結果的可靠性。

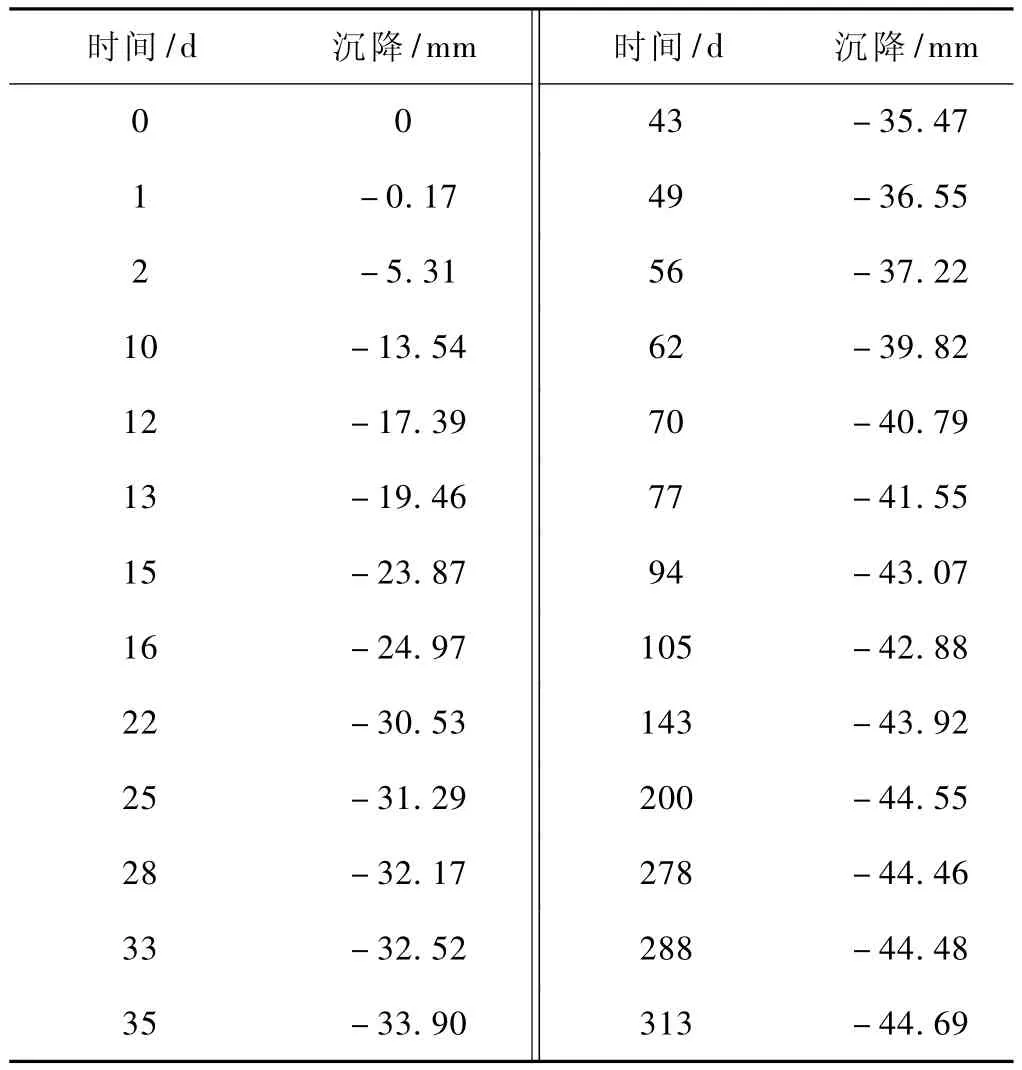
表2 李窯路基試驗段A區路基中心CFG樁頂沉降觀測數據

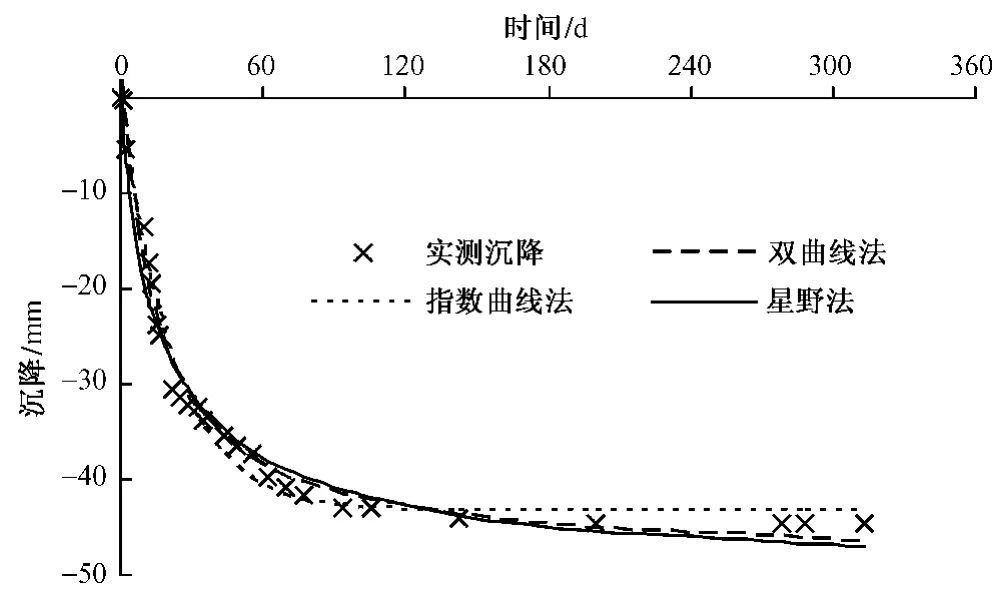
圖2 李窯試驗段A區0～313 d沉降數據擬合結果

如圖3，雙曲線法和星野法的尾段殘差趨于增大，說明當前的最終沉降預測值偏于安全。與之對應，指數曲線法尾段殘差趨于減小，說明當前的最終沉降預測值偏于不安全(第278 d后殘差變化趨勢變緩為預壓土卸載所致)。最有可能的最終沉降介于－48.7～－43.4 mm之間，沉降評估使用－48.7 mm作為預測值是可靠的。

圖3 李窯試驗段A區0～313 d沉降擬合殘差分布

圖4為李窯試驗段 A區由0～105 d(靜置期89 d)沉降觀測數據擬合得到的殘差分布。此時，雙曲線法、指數曲線法和星野法得到的最終沉降分別為－51.4 mm、－41.9 mm和 －57.6 mm，相關指數 R2分別為0.986 7、0.987 1和0.972 9。由殘差分布圖尾段1個多月連續的4次觀測殘差趨勢可見，此時的星野法預測值偏于安全，指數曲線法預測值偏于不安全，雙曲線法稍偏于安全，可以作為此時的預測值。

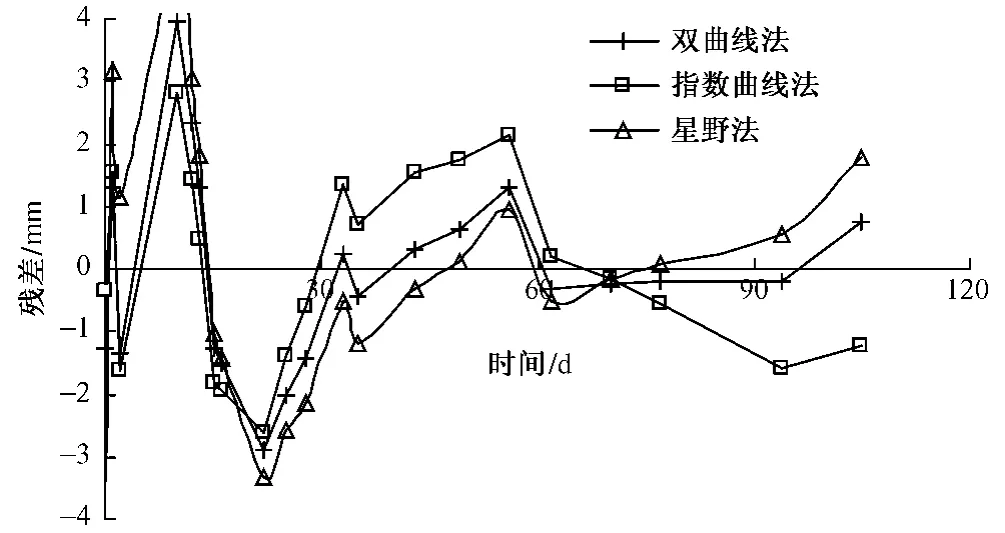
圖4 李窯試驗段A區0～105 d沉降擬合殘差分布

由此可見，借助殘差分析可以較早地判斷出當前的預測值是否偏于安全，有利于沉降評估工作的快速推進。殘差分布圖尾段趨勢分析時，尾段所涵蓋的時間不宜少于1個月，觀測值不宜少于4組。

4 結語

根據新建鐵路線下工程沉降評估工作的特殊性，提出沉降預測的三個特點:對可靠性要求較高，要求數學模型具備連續性和單調性，要求數學模型具備有界性。

工后沉降預測是遠期預測，目前的灰色理論和神經網絡方法尚不能完全適應，不建議在沉降評估中使用這兩種方法。

使用回歸分析法預測模型時，可以結合殘差分析判斷沉降預測的可靠性。

[1] 張在明.巖土工程的工作方法［C］//第二屆全國巖土與工程學術大會論文集.北京:科學出版社，2006.

[2] 中華人民共和國鐵道部.客運專線鐵路無砟軌道鋪設條件評估技術指南［S］.北京:中國鐵道出版社，2006.

[3] 付宏淵.高速公路路基沉降預測及施工控制［M］.北京:人民交通出版社，2007.

[4] 何曉群，劉文卿.應用回歸分析［M］.北京:中國人民大學出版社，2007.

[5] 王麗琴，靳寶成，楊有海.黃土路堤工后沉降預測新模型與方法［J］.巖石力學與工程學報，2007，26(11):2370-2376.

[6] 尤昌龍.無砟軌道鋪設條件——線下工程沉降變形分析評估［J］.鐵道工程學報，2008(增):110-129.

[7] 鞠國江.無砟軌道鐵路路基沉降觀測及評估［J］.鐵道標準設計，2009(8):19-22.

[8] 潘林有，謝新宇.用曲線擬合的方法預測軟土地基沉降［J］.巖土力學，2004，25(7):1053-1058.

[9] 梅國雄，宰金珉，殷宗澤，等.沉降—時間曲線呈“S”形的證明——從一維固結理論角度［J］.巖土力學，2004，25(1):20-22.

[10] 許永明，徐澤中.一種預測路基工后沉降量的方法［J］.河海大學學報，2000(5):110-113.

[11] 趙國堂，馬建林，彭聲應，等.高速鐵路CFG樁不同結構形式下地基沉降—時間發展規律的試驗研究與預測［J］.鐵道建筑，2009(7):62-65.

[12] 王勝濤，楊廣慶，薛曉輝.高速公路路基沉降監測技術研究［J］.鐵道建筑，2008(2):76-78.

[13] 呂秀杰，王卓琦.高速公路雙曲線法推算工后沉降誤差分析［J］.鐵道建筑，2008(9):61-63.

[14] 曾俊鋮，張繼文，彭志鵬，等.京滬高速鐵路CFG樁復合地基沉降預測分析［J］.鐵道建筑，2009(7):69-71.

[15] 薛曉輝，周喬勇，梁偉.滑動式沉降儀觀測路堤沉降試驗研究［J］.鐵道建筑，2007(11):52-53.