應用時間序列模型分析長武塬區地下水水位的變化特征*

張盼,劉文兆,2

(1.西北農林科技大學資源環境學院,陜西楊陵712100;2.中國科學院水利部水土保持研究所,陜西楊陵712100)

地下水是水資源的重要組成部分,目前我國大部分地區的地下水形勢不容樂觀。長武塬區地下水資源貧乏,長期以來存在的盲目開發和超量開采造成了地下水位持續下降,進而造成水資源供需矛盾加劇。因此,研究地下水動態變化規律,預測未來變化趨勢,對水資源利用管理具有重要的意義。

時間序列分析是應用比較廣泛的一種科學分析方法。由于這種方法比較簡單,而且可以定時定量地推測事物的未來發展,所以對預測、決策具有較高的實用價值[1]。近20年來,時序分析理論已應用于地下水資源評價、預報和管理之中。常用于地下水位預報的時序模型有自回歸模型(AR),滑動平均模型(MA)、自回歸滑動平均模型(AR-MA)。近年來隨著計算機技術的發展和廣泛應用又發展了多種模型,如求和自回歸滑動平均模型(ARIMA)、乘積型季節性模型、組合模型、混合模型以及門限模型、混沌時間序列模型等[2-5]。這些模型應用靈活方便且具有較高的模擬精度,給大區域地下水動態預報分析帶來了極大的便利。

1 研究區概況

1.1 自然地理概況

研究區所在的長武縣位于陜西省咸陽市轄區西北角,西、北、南三面分別與甘肅省涇川縣、寧縣、正縣、靈臺縣接壤,全縣土地面積為583 km2。地勢由西向東傾斜,海拔高度847～1 274 m,該地區系典型的黃土高塬溝壑區[6],屬暖溫帶半濕潤大陸性季風氣候,降水集中在7-9月,占全年降水總量的55%以上。全縣有涇河、黑河、南河3條河流。涇河沿縣北向東后折向東南流去,境內流長56 km,年平均流量42.2m3。黑河、南河年平均流量為10m3/s以下。三條河流將長武縣分割為巨家塬、棗元塬和長武塬三部分[7-8]。其中長武塬土地面積為297.4 km2,塬面積為101.6 km2,塬面和溝坡面積分別占34.2%和65.8%,地下水埋深30～80 m[7,9]。

1.2 水文地質概況

長武縣屬祁、呂、賀山子型構造的聯合復合區。基巖大部分被黃土覆蓋,基底是巨厚的中生界沉積砂頁巖,平鋪緩斜,褶皺輕微,自下而上依次為三迭系、侏羅系、白堊系[6]。研究區主要由第四系新老黃土組成,自上而下為馬蘭黃土、離石黃土、午城黃土。塬區潛水含水層是以風積黃土狀亞砂土為主的孔隙-裂隙含水層,有良好的儲水空間;且每層古土壤均含有鈣質結核,含水層底部鈣質結核膠結致密,作層狀分布,形成較好的隔水層,構成一定儲水條件,是黃土塬區主要的潛水含水層,含水深度為20～100 m。在長武北塬區中心部位,塬面平坦開闊,地下水埋深25～60 m,含水層厚度 60～80 m,為中等富水潛水層;在塬區周邊,由于溝谷對地下水的疏干作用,地下水埋深則在60～85m以上,含水層厚度也相應變薄。在南部塬區,由于地形破碎,地下水賦水條件很差,地下水埋深較深,人畜飲用水困難。

塬區地下水埋深多為40～100 m,四周均被切割至基巖的溝谷所包圍。黃土中地下水位高于溝谷中地表水流,更高于基巖中的承壓水,因此無地下側流補給,降水垂直入滲是塬面地下水補給幾乎唯一的來源[7,10]。

2 材料與方法

2.1 數據獲取

選取研究區當地水利局地下水監管站3口水位埋深監測井長期觀測資料進行分析。其中,551井位于研究區西段洪家鄉風口村,552井位于研究區中段地掌鄉代苓村,555井位于研究區東段彭公鄉豐頭村。每5天(即每月1日,6日,11日,16日,21日,26日)用測繩量測監測井水位。

2.2 時間序列分析法

時間序列,也叫時間數列、歷史復數或動態數列。它是將某種統計指標的數值,按時間先后順序排到所形成的數列。時間序列預測法就是通過編制和分析時間序列,根據時間序列所反映出來的發展過程、方向和趨勢,進行類推或延伸,借以預測下一段時間或以后若干年內可能達到的水平。在生產和科學研究中,對某一個或一組變量 x(t)進行觀察測量,將在一系列時刻t1,t2,…,tn(t為自變量且t1＜t2＜…＜tn)所得到的離散數字組成序列集合x(t1),x(t2),…,x(tn),稱之為時間序列,這種有時間意義的序列也稱為動態數據。這樣的動態數據在自然、經濟及社會等領域都很常見。

時間序列分析是根據系統觀測得到的時間序列數據,通過曲線擬合和參數估計來建立數學模型的理論和方法。它把系統看作一個暗箱,不考慮外界因素的影響,假設預測對象的變化僅與時間有關,根據客觀事物發展變化過程中的內在延續性進行預測。這種內在延續性反映了外部影響因素綜合作用下對象的變化過程。時間序列預測過程只依賴于歷史觀測數據及其數據模式,從而使預測研究更為直接和簡潔。時間序列分析主要用于:系統描述、系統分析、預測未來、決策和控制。

在對地下水系統的研究中 ,把實體系統作為直接研究對象極其困難。一般通過系統模型來描述實體系統的特性及其變化規律[11]。應用時間序列(簡稱“時序”)分析法進行水位預報,正是將地下水系統視為“黑箱”或“灰箱”,根據地下水位動態觀測資料,提取和分析歷史資料本身所蘊涵的信息,找出其規律,并利用這些規律,達到預報未來的目的,無須再進行專門的試驗來獲取其它參數,這給大區域地下水動態預報分析帶來了極大的便利,并且,該方法易于掌握,計算工作量小,易于應用推廣[12]。

如今,SAS的豐富數據采集、數據管理、數據分析和信息展現的能力,使之成為決策支持的最好工具。其中,SAS/ETS提供的基本時間序列預測方法包括:逐步自回歸模型、指數平滑模型和季節性模型[13]。用SAS軟件所提供的這三種方法對研究區地下水位建立模型,經過比較,選取了適合研究區的最優模型——指數平滑模型。

2.2.1 時間序列模型基本組成 由于地下水水位數據具有趨勢性,周期性和一個靜態分量,一個非穩定的時間序列模型可以適用于地下水位數據的分析。根據地下水水位數據的特征,一個地下水非穩定的地下水時間序列模型可以用以下疊加形式表示:

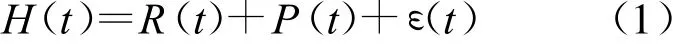
式中:H(t)——地下水位埋深;R(t)——趨勢項;P(t)——周期項 ;ε(t)——隨機分量 。

從已知序列(觀測值)H(t)(t=1,2,3,…,n)中提取各分量。提取的順序為:趨勢分量R(t)、周期分量P(t)和隨機分量ε(t)。各分量的數學模型建立后,再將其線性疊加,就得到了地下水水位埋深預測模型H(t)。其中,t為地下水水位監測周期,一個單位的t表示一個地下水水位監測周期,取決地下水水位監測頻率。

(1)趨勢分量R(t)的確定。對于趨勢分量R(t)可以用多項式逼近,即可得到估計值R'(t)。

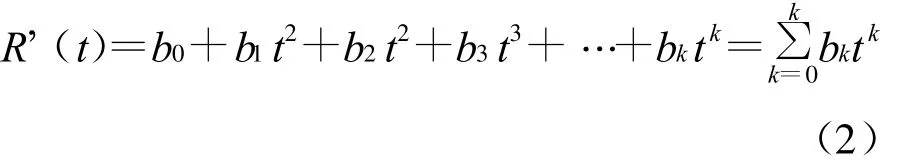
采用多元回歸方法確定待定系數b0,b1,b2,b3,…,bk和階數k。同時需要計算趨勢曲線擬合的相關系數R。

(2)周期分量P(t)的確定。趨勢函數確定后,對去除趨勢分量后的部分p(t)進行周期項分析,即:

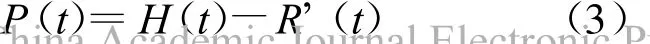
采取諧波分析法進行周期分量的分析提取。對序列P(t),可以用L個諧波疊加的形式表示其估計值為

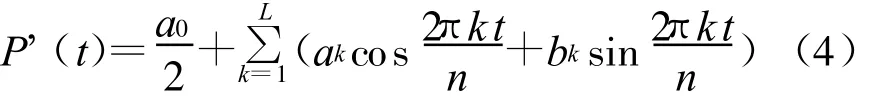
式中:P'(t)——序列 P(t)的估計值;L——諧波個數,取n/2的整數部分;k——諧波序號,k=1,2,…,L;Tk=n/k,也就是第k個諧波的周期;ak,bk——傅立葉系數,計算式為

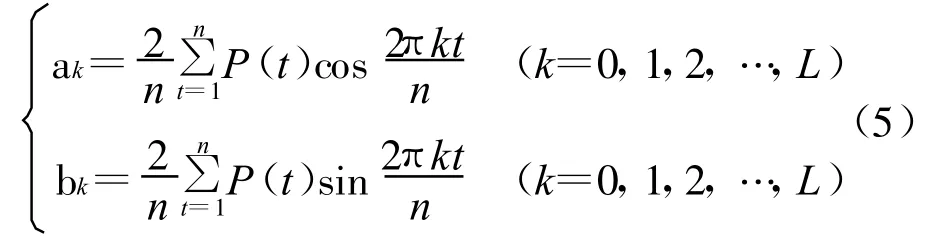
(3)隨機分量ε(t)的確定。去除趨勢分量和周期分量的部分既是隨機分量部分ε(t)。

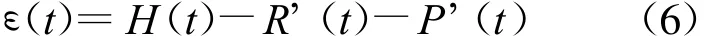
式中:ε(t)——一平穩隨機系列項,可直接對其用自回歸模型求解。其自回歸模型為

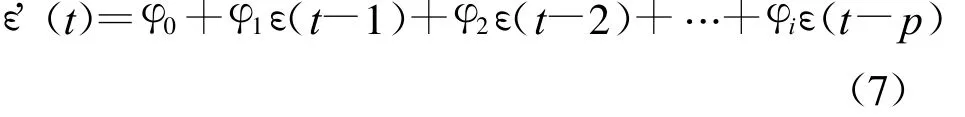
式中:p——模型階數;φi——模型自回歸系數,i=0,1,2,…,p。

對某一階數的自回歸模型,類似多元回歸計算可求得自回歸系數φi。本文采用了AIC準則[4]來確定模型的階數,即:

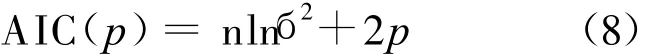
使上式值最小時所對應的 p值為最佳階數。

式中:n——序列數據總個數;б2——式(7)階數為 p時殘差的方差。(4)時間序列模型。將上述趨勢分量,周期分量,隨機分量線性疊加,即可得到地下水位的總預測模型:

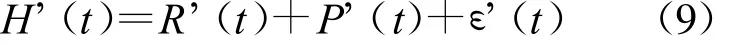
2.2.2 模型的檢驗 應用SAS軟件自帶的時間序列模型對研究區地下水位進行模擬后,對其精度進行檢驗,進而確定其是否合理。本文采用后驗差方法[3,6]對模型進行精度檢驗。通過后驗差比值C和小誤差頻率P來檢驗(見公式10)。

式中:S1——原始數據(實測值)方差的開方;S2——殘差(絕對誤差)的標準差;ξ(k)——殘差;ˉξ— —殘差均值。

上述兩個指標C,P把預測的等級劃分為四等,如表1所示,通常用其作為檢驗預測模型的精度。

表1 預報精度評價標準

如果P,C值都在允許范圍內,則模型可用于計算預報值,否則需要對模型進行檢查、分析和重新調參。

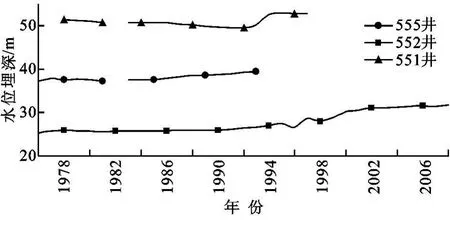
圖1 研究區地下水位埋深概況

2.3 所選監測井水位埋深概況

分別選取551井,552井和555井1976-1993年,1976-2008年和1978-2003年的水位觀測資料進行分析。(其中552井監測情況最好,1976年至今資料保存完備;551井的監測資料自1993年后部分丟失,故只選連續較好的前18年監測資料進行分析;555井由于干枯而于2003年停測,期間1996年資料丟失。)

研究區三口井水位埋深情況見圖2。由圖可以看出這三口監測井中552井水位較淺水位埋深不超過35 m,555井水位較深,水位埋深大于50 m,551井水位埋深則處于35～40 m。

3 時間序列分析在研究區地下水位預報中的應用

3.1 模型的應用

利用SAS/ETS中的指數平滑模型對研究區552井(1976-2008年)、551井(1976-1992年)及555井(1978-2002年)月平均地下水位數據進行模擬,擬合結果見圖2。并分別得到觀測井552井2009年各月(1-8月)水位埋深預測值,551井1993年各月(1-9月)水位埋深預測值,以及555井2003年各月水位埋深預測值,與實測值進行對比,用以評價模型的預測效果。其決定系數分別為:R2=0.999(552井),R2=0.962(551井),R2=0.997(555井)。擬合結果及誤差分析見表3,預測結果及誤差分析見表4。

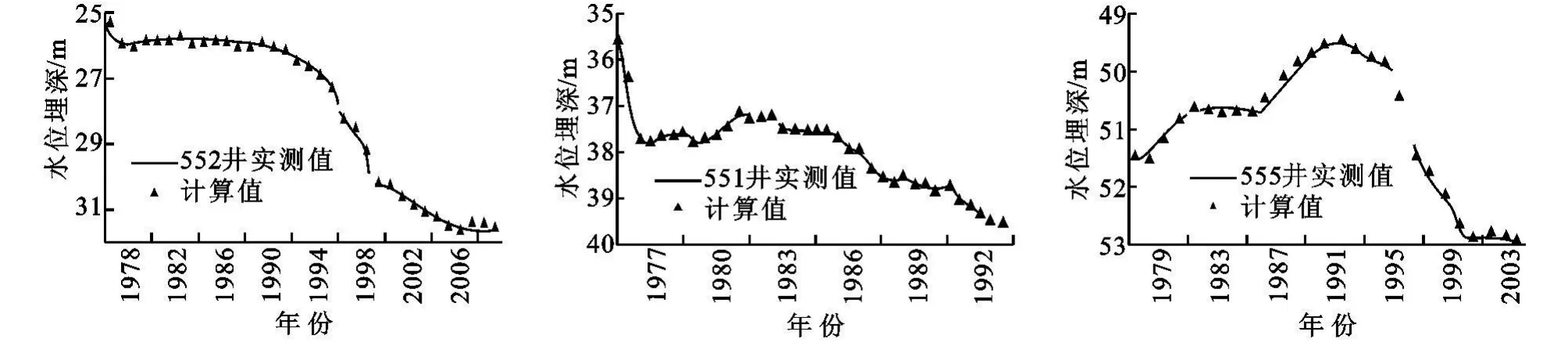
圖2 模型計算值與實測值擬合曲線

由552監測井2003-2008年的計算值與實測值的擬合曲線(圖2)可以更清楚地觀察模型對該井的計算值與模擬值的擬合情況。表1可明顯看出,該模型的擬合精度很高,其最大絕對誤差(殘差)為0.06 m,最小絕對誤差為5.67×10-5m。相對誤差大多小于0.1%,個別稍微大點的值也不超過1%。由該模型對研究區551監測井和555監測井的模擬預測擬合曲線圖(圖2)可以看出,兩口井的水位也是逐年下降的。

3.2 模型的檢驗

運用公式(10)對模型的預測精度進行計算得到P值和C值(見表2),對照表1可知,SAS軟件自帶的時間序列模型對研究區這三口井的預測精度均達到理想的預測等級。

同時,由表3可以看出,指數平滑模型對于551井的模擬預測效果較理想,擬合精度好。其絕對誤差最大值為0.14 m,最小值可達0.001m。相對誤差一般都小于0.4%,最大也不超過1%。該模型對555井的井水水位擬合程度同樣較高。其中,絕對誤差(殘差)最大為0.03 m,最小甚至不足0.001 m。相對誤差大多數在0.55%之下,個別較大的值也不超過1%。

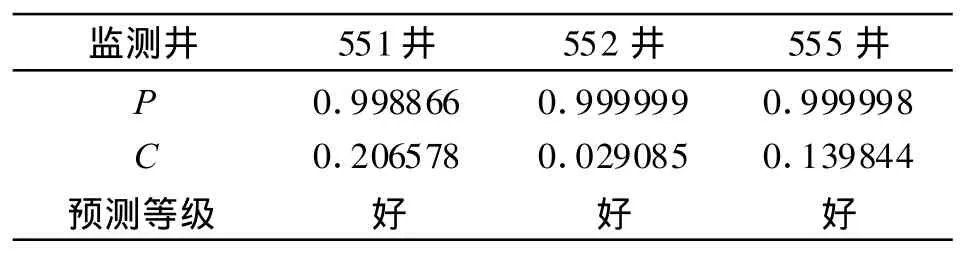
表2 精度檢驗結果表

在把已建立的模擬模型用于預報前,也要進行精度檢驗,本文用未參加建模的水位資料(551井的1993年,552井的2009年,555井的2003年)進行后驗預測檢驗。可得到551井1993年、552井2009年以及555井2003年各月水位埋深預測值。其后驗預測結果見表4。

表4中可以看出,552井預測的絕對誤差(殘差)最大值為0.12 m,絕對誤差的最小值可達1.23×10-3m。相對誤差一般都不超過1%。該模型對551井的預測精度較之552井稍好些。其絕對誤差(殘差)最大值為0.13 m,最小值可達9.59×10-4m。相對誤差均不超過0.4%。對555井的預測其絕對誤差(殘差)最大值為0.15 m,最小值達到3.38×10-5m。其相對誤差最小值為6.39×10-5%,最大值不超過0.3%。可以看出,該模型對研究區監測井的擬合及預測精度都較高。

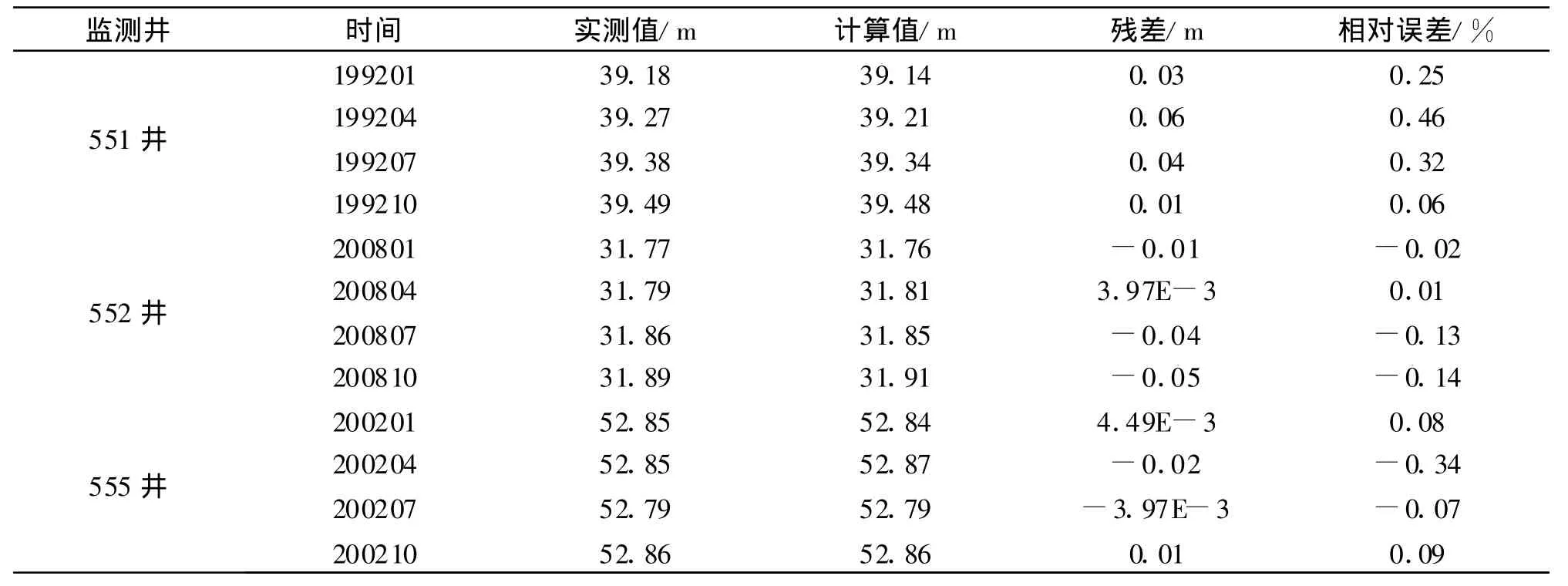
表3 模型計算結果與誤差分析

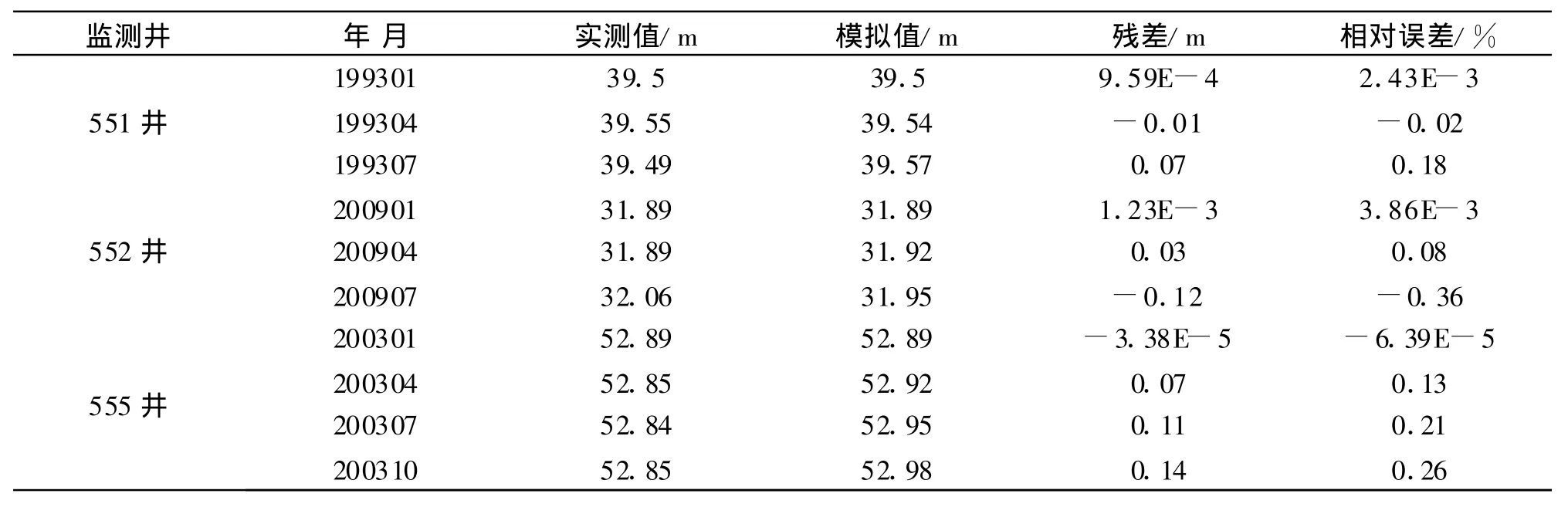
表4 模型模擬結果與誤差分析

3.3 分析與討論

時間序列分析是把系統看作一個暗箱,不考慮外界因素的影響,假設預測對象的變化僅與時間有關,根據客觀事物發展變化過程中的內在延續性進行預測。但是利用地下水系統過去的資料進行建模是通過系統過去的規律預測未來,當系統的某些因素發生較大變化時,模型預報誤差將增大,因此建模時需要考慮到系統因素的變化。影響研究區地下水變化的主要因素如下。

(1)黃土區地下水埋深大部分為40～100m,且降水幾乎是唯一的補給源[7,14-15]。研究區地下水補給來源為當地降水,降水一方面轉化為土壤水緩慢補給給地下水,年補給量約為10mm;另一方面通過降雨形成徑流,在塬面的黃土碟、黃土胡同或者居民開挖的澇池等負地形地段匯集后補給地下水,補給滯后時間多為30～40 d,也可能有較短的為10 d左右,受降雨量、降雨強度以及補給通道濕度等因素影響[7]。研究區50 a中(利用長武縣氣象局1957-2006年的逐日降水數據分析),豐水、平水和枯水年分別為18 a、12 a和20 a,豐水年和枯水年數比較接近[16]。且降水年際分布不均,年平均降水量為578.7mm(1957-2006年),年最大降水量為954.3 mm(2003年),年最小降水量為 296.0 mm(1995年),相差657.3 mm,表現出年際變化大的特點。

(2)研究區塬區的機井數量由1993年101眼增加到2008年181眼,由于研究區塬面積有限,以后塬面上的機井數量不再會有較大變化。與此同時,地下水源開采量由1999年的1.84×106m3增加到2008年的3.31×106m3。1998年至2007年10 a間年均降水量為589.39 mm,除2004年年降水量(493.7 mm)不足500mm外,其余年份年降水量均超過500mm,且2003年達到954.3 mm。而研究區地下水位埋深卻整體處于下降趨勢,是由于人為開采量增加導致的。由于塬面上的機井數量今后不會發生較大變化結合當地部門對地下水資源保護的重視,日后將會有計劃的對地下水進行開采。但是隨著社會的發展,人口的增長,工農業用水依然在不斷增長,故該因素為影響研究區地下水變化的又一重要因素。

上述這些因素在時序建模中沒有涉及到,因此,未來某些因素發生較大變化時,模型預報誤差會增大。所以,應及時把新得到的實測數據加到原序列中,實時更新模型,以提高預測的精度。

由上述分析可知,SAS/ETS中指數平滑模型可以用于研究區地下水位的研究。其擬合精度高,且需要的數據不多,獲取也簡單,可以考慮用于研究區地下水位動態變化規律的研究。

4 結論

(1)運用SAS軟件自帶的時間序列分析法中的指數平滑模型分別對長武塬區三口監測井建立地下水位埋深模型。結果表明,擬合精度和預測精度均較高。該模型較全面地反眏了地下水位動態變化規律,且計算簡單,所需資料較少,易于獲得,是一種較好的模擬預測模型,能很好地應用于分析地下水位動態的趨勢性和周期性以及進行地下水埋深預測,為區域地下水的合理開發利用及水資源規劃提供可靠依據。

(2)通過對趨勢項的分析可知,552監測井32 a間水位埋深由25.3 m(水位標高1 163.12 m)上升到31.84 m(水位標高1 156.58m),即水位降幅達到6.54 m,年均下降為0.2 m。由圖可知,1976-1995年間,該井水位下降緩慢,這20 a間的水位年均下降為0.1 m。1996-2008年間,呈明顯下降趨勢,年均下降0.4 m。尤其是近幾年,地下水位下降幅度越來越大,從模擬結果可看出,如果不進行科學管理,控制開采,還有繼續下降的趨勢。

(3)通過對模型中的周期項分析可知,該區地下水位動態具有兩個主要的周期成分。一個周期長度為一年,反映了一年內地下水位的季節性周期變化。另一個周期長度為7.4～10 a,并且隨著時間的增長周期也逐漸增長,這與該地區氣候(主要是降水量)多年的周期性變化情況大體一致。

(4)利用地下水系統過去的資料進行建模是通過了解過去的規律對未來進行預測,當系統的某些因素在未來時刻有較大變化時,模型預報誤差將增大。因此,要及時把新得到的實測數據加到原序列中,實時更新模型,以提高預測的精度。

鑒于研究區特殊地形及氣候的影響,地下水的開發利用在當地工業和生態用水中占據重要地位,有的地方甚至成為唯一的水源。因此建議當地相關部門加強對地下水位變化規律的研究,掌握預測水位未來變化趨勢的方法,合理規劃和開發利用地下水資源。

[1] 董殿偉,劉久榮,林沛,等.時間序列分析法在地下水水位預測中的應用[J].城市地質,2007,2(4):29-32.

[2] 丁濤,周惠成,黃健輝.混沌水文時間序列區間預測研究[J].水利學報,2004,35(12):15-20.

[3] 楊位欽,顧嵐.時間序列分析與動態數據建模[M].北京:北京工業學院出版社,1986:8-14.

[4] 楊志霞.時間序列模型在深層地下水水位預測中的應用[J].河北工程技術高等專科學校學報,2000(3):34-38.

[5] 楊忠平,盧文喜,李平.時間序列模型在吉林西部地下水動態變化預測中的應用[J].水利學報,2005,36(12):1475-1479.

[6] 中國科學院水利部水土保持研究所.土地資源及生產力研究[M].北京:科學技術文獻出版社,1991:4-6.

[7] 王銳.基于環境同位素的黃土塬區降水-土壤水-地下水轉換關系研究[D].北京:中國科學院研究生院,2007.

[8] 長武縣農業區劃委員會.陜西省長武縣農業資源調查和農業區劃報告集[M].長武:長武縣印刷廠,1985.

[9] Liu Wenzhao,Li Zhi,Wang Rui,et al.Dynamic change of groundw ater level in Changw u tableland region on the Loess Plateau of China[C]//Proceedings of 3rd Internationna lWorkshop on Yellow River Studies.Japan:Kyoto,2007.

[10] 咸陽市水政水資辦,長武縣水政水資辦.陜西省長武縣水資源評價及開發利用現狀分析[M].咸陽:咸陽市地下水管理監測站印制,1993.

[11] 盧曉燕,施鑫源,眭克仁.地下水資源系統時序管理模型[J].工程勘察,1999(4):35-38.

[12] 楊金忠,蔡樹英.一種區域地下水預報的時間序列分析方法[J].武漢水利電力大學學報,1996,29(4):6-10.

[13] 張小娟,蔣云鐘,秦長海,等.時間序列分析在地下水位預報中的應用[J].南水北調與水利科技,2007,5(4):40-42.

[14] 楊文治,趙沛倫,張啟元.不同濕度條件下土壤水分的蒸發性能和移動規律[J].土壤學報,1981,18(1):24-37.

[15] 李玉山.黃土區土壤水分循環特征及其對陸地水分循環的影響[J].生態學報,1983,3(2):24-37.

[16] 陳杰,劉文兆,王文龍,等.長武黃土高塬溝壑區降水及侵蝕性降雨特征[J].中國水土保持科學,2009,7(1):27-31.