基于粒子群算法的預編碼設計

劉小聰，劉洪武

（南昌航空大學 信息工程學院，江西 南昌 330063）

0 引言

多輸入多輸出(MIMO)系統利用空分復用技術可以獲得很高的頻譜效率，能在多徑環境下能獲得更大的分集增益，同時提高系統容量[1]。然而空間冗余的缺乏使得空分復用技術不再適用于虧秩MIMO信道[2-3]，并且在多用戶MIMO系統的下行鏈路中，傳輸環境復雜導致了在接收端不能完成協作譯碼、檢測[4]。所以為了簡化接收機和避免接收端固有的噪聲增強特點，發射端可以在獲得信道信息情況下對用戶間的干擾進行預消除，使得接收端可以不需要譯碼而直接接收[5-6]。

預編碼技術是將輸入數據流分成M個子流，再通過矩陣乘法將輸入M個數據流映射到所有發射天線進行發射[7]，該技術能有效對抗MIMO信道虧秩問題，同時降低系統錯誤概率。在傳統的預編碼方案中一般采用對信道進行奇異值分解(SVD)、幾何均值分解(GMD)[8-9]。提出一種基于粒子群算法(PSO)的預編碼矩陣搜索方案，根據錯誤概率上界和最小信噪比之間的關系采用最小誤符號準則來衡量系統性能。

1 系統模型

在多用戶MIMO系統下行鏈路系統中，考慮有K個用戶，每個用戶采用相同星座符號集合Ω進行獨立調制, 在時刻t，用戶 k發射符號為b (t)=[b(t),b(t),…,(t)]T，

k k ,1k ,2（k=1,2,…,K）。用戶k發射符號 bk(t)經過 M×Tk維預編碼矩陣編碼后產生矢量 xk(t)，M為發射天線數，Tk為發送符號長度，假設預編碼矩陣為Wk(t)，則：

εk為用戶k發射符號能量，假設M≥Tk，經PSO預編碼搜索編碼矩陣相乘后，矢量 xk(t)的第q個元素 xk,q(t)映射到第q跟天線進行發射。用戶k的發射天線q，接收天線p之間信道均服從N(0,1)。如果m≠p或者n≠p，則(t)獨立于(t)。任意第p跟接收天線上疊加噪聲為 n (t)，服從 k,p N(0,)，且m≠p時，n(t)獨立于n(t)。用戶 k接收 k,p k,m天線數為 Rk，且假設 Rk≥Tk，則用戶k接收基帶信號為：

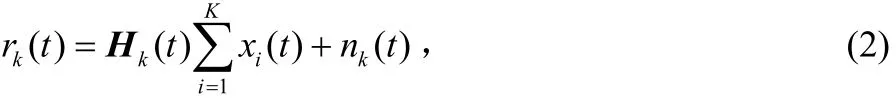
其中 Gk為 Tk×Rk維線性解碼矩陣。因為在下行傳輸過程中，移動臺之間距離不定，所以假設用戶k接收到的信號無其他用戶干擾，則接收信號可以寫成：

接收通過線性解碼器有：

由最小子流的信噪比SNR可推導得到系統平均符號錯誤概率性能。接收后第l，l ∈( 1,2,… ,T )層數據子流 S 為[10]：

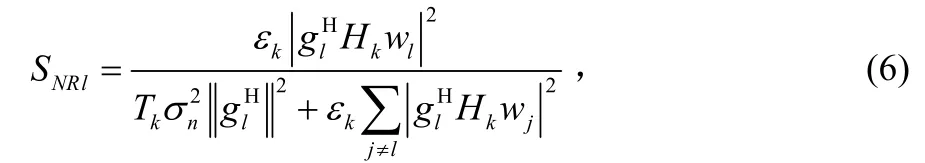
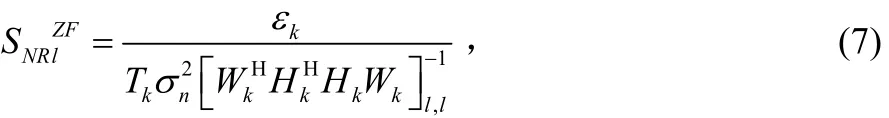
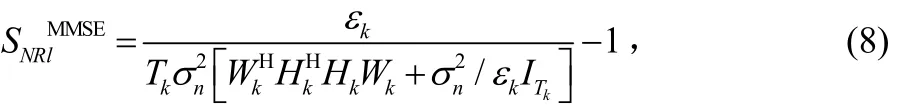
其中：

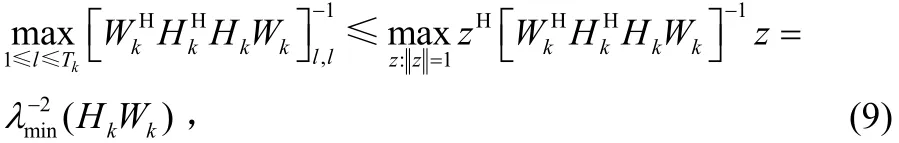
其中 el是ITk的第l列，λ()表示求奇異值。聯合式(7)、式(8)和式(9)得到：

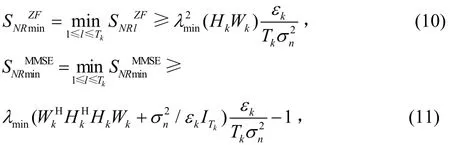
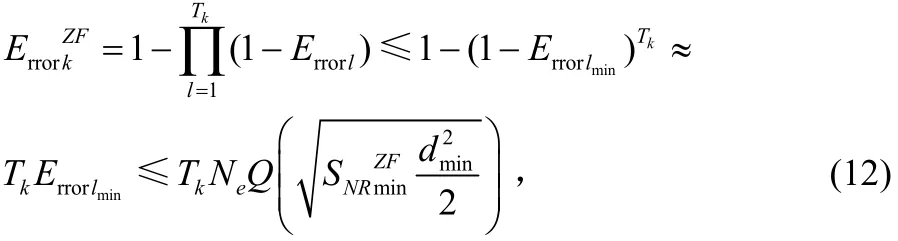
對于MMSE接收機有：

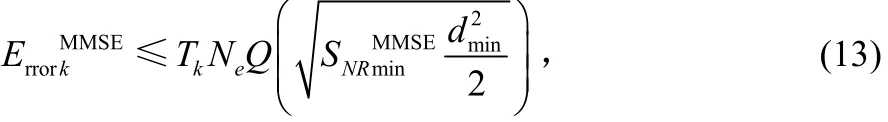
其中，dmin為發射星座符號間最小距離，Ne為發射星座圖符號集Ω中最近鄰居數。因此，對給定調制方式和εσ2，并k n且已經獲得信道信息情況下，對于求 Errork越小，等價于求使越大的W與使最大的W，約束條件為WHW=I。在傳統的預編碼方案中采用對信道H進行SVD分解求W。

2 基于粒子群算法的預編碼

粒子群算法是一種有效的全局尋優算法，他是基于群體智能理論的優化算法，通過群體中粒子間的合作和競爭產生的群體智能指導優化搜索[11]。一個基本的粒子種群包括多個粒子，每個粒子在自由空間有記憶的無規律變化。粒子群算法中將每一個可能產生的解表述為群中的一個粒子，每個粒子有自己的速度和位置向量，以及一個由目標函數決定的適應值，所有粒子在搜索空間以一定速度飛行，通過追隨當前搜索到的最優適應值來尋找全局最優。

在n維空間中有M個粒子，每個粒子的位置表示一個潛在的解。設 Xi= ( xi,1, xi,2, …,xi,n)表示粒子 i的當前位置，Vi= ( vi,1, vi,2,…,vin)表示粒子 i的當前速度，Pi=(pi,1, pi,2,…,pin)表示粒子i所歷經最佳位置，即 Pbest。Pg表示群體中所有粒子歷經的最佳位置。則對于每一代，粒子i的第j維的進化方程：

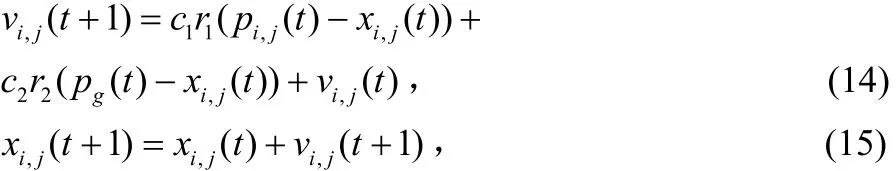
其中 c1，c2為加速常數，r1，r2為 0，1范圍內的隨機數。在多用戶下行傳輸預編碼過程中，M ×Tk維矩陣Wk的一種可能表示一個粒子，Errork表示單個粒子的適應度。其搜索過程如下：

步驟① 初始化粒子種群W = [w1,w2,… ,wn]，wi(i=1,2,…,n )表示第i個粒子，n為群體規模。在允許范圍內隨機設置粒子的位置和速度。并對每一個粒子計算初始化位置的最佳適應度,記為(i=1 ,2,…,n )，以及初始化的最佳位置，初始化全局最佳位置；

步驟② 根據式(14)，式(15)更新粒子速度和位置；

步驟③ 再次計算更新后的粒子的適應度Errori，當前位置ip和當前全局最優位置gp；

3 仿真結果

現對平坦衰落信道迫零檢測和最小均方誤差檢測兩種檢測方案采用粒群算法進行預編碼設計進行仿真。結果如圖1和圖2所示。

圖1中接收端采用迫零檢測方案，圖2中接收端采用最小均方誤差檢測。仿真時粒子種群為10，迭代次數為10，發射天線4，接收天線3，用戶數2。采用4QAM調制方式，符號間距離為，對10 000幀求平均得最終符號錯誤概率。-3 dB信噪比情況下，迫零檢測情況下的PSO預編碼方案、SVD預編碼方案和未編碼系統誤符號率基本接近，最小均方誤差檢測情況下則PSO預編碼方案誤符號率未編碼系統性能高出0.1 dB。在0 dB信噪比情況下，PSO預編碼方案比未編碼情況性能高約1 dB，比傳統SVD預編碼方案性能高約0.3 dB。在10 dB信噪比情況下PSO預編碼方案比未編碼系統性能高約3 dB，比SVD預編碼方案系統性能高約1.7 dB。

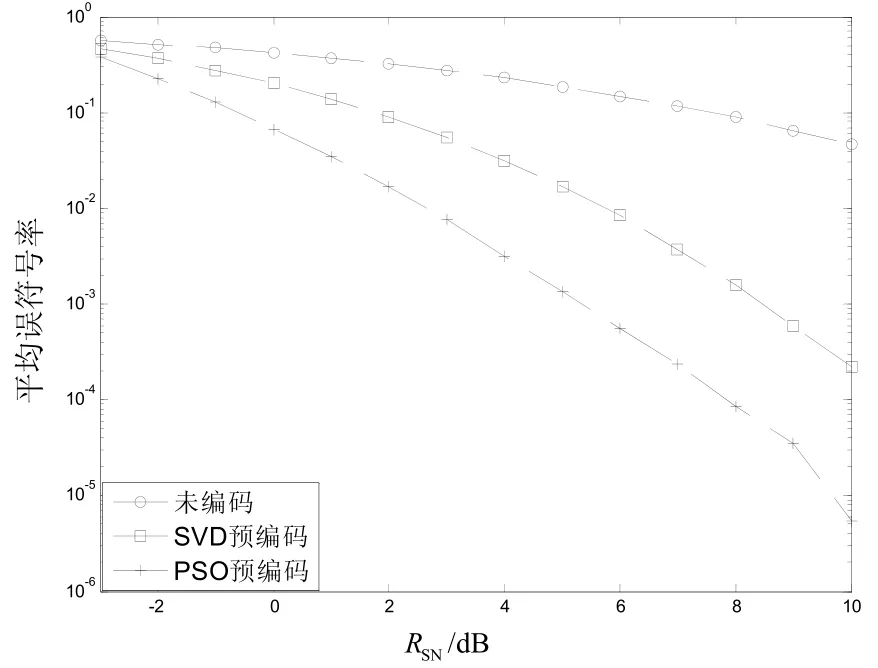
圖1 4×3系統ZF檢測預編碼性能比較

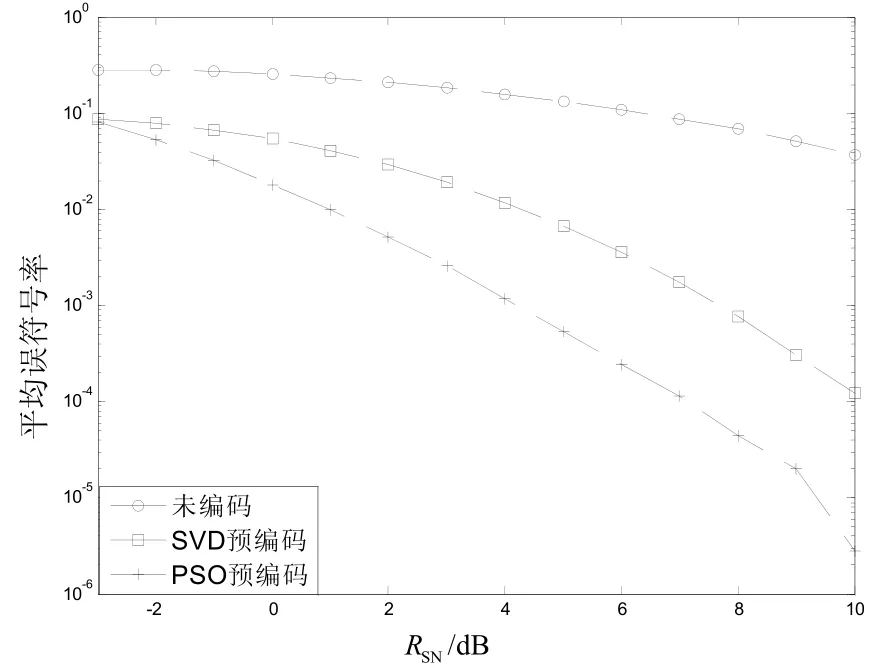
圖2 4×3系統MMSE檢測預編碼性能比較

4 結語

利用粒子群算法對多用戶MIMO下行傳輸系統進行預編碼，仿真結果表明該算法比傳統預編碼方法性能更優越。由于粒子群算法是一種優化搜索算法，其編碼復雜度相比傳統預編碼方法要大，因此在以后的研究過程中可以著重改進其復雜度和收斂速度。

[1] GOLDSMITH A,JAFAR S A, VISHWANATH S. Capacity Limits of MIMO Channels[J].IEEE Journal on Selected Areas in Conmmunications,2003(21):684-702.

[2] LI J W,LI D B.Limited Feedback Open Loop Precoding in the Downlink Relay Multiuser MIMO System[C].USA:IEEE,2009:1-4.

[3] GORE D A,NABAR U R. Selecting an Optimal Set of Transmit Antennas for a Low Rank Matrix Channel[C].USA:IEEE,2000:2785-2788.

[4] 李昊,徐昌慶.多用戶 MIMO下行鏈路中線性預編碼器和譯碼的聯合優化[J].通信技術,2009,42(02):1-3.

[5] SCAGLIONE A,STOICA P, BARBAROSSA S. Optimal Designs for Spacetime Linear Precoders and Decoders[J].IEEE Transactions Signal Processing,2002,50(05):1051-1064.

[6] XIN Y, WANG Z, GIANNAKIS G B. Space-time Diversity Systems based on Linear Constellation Precoding[J].IEEE Transaction Wireless communication,2003,2(02):249-309.

[7] ZHANG J, WU Y, XU M. Linear Transmitter Precoding Design for Downlink of Mulfuser MIMO Systems[J].Electronics Letters,2005,41(14):811-813.

[8] SCHMIDT D A, JOHAM M, UTSCHICK W. Minimum Mean Square Error Vector Precoding[J].Proceedings of PIMRC,2005(01):107-111.

[9] CHEN R, JEFFREY G, HEATH ROBERT W. Multiuser Space-time Block Coded MIMO System with Downlink Precoding[C].USA:IEEE,2004:2689-2693.

[10] HEATH ROBERT W, Jr.Antenna Selection for Spatial Multiplexing Systems with Linear Receivers[J].IEEE Communications Letters,2001(05):142-144.

[11] 胡宏梅,浦靈敏.基于粒子群算法的碼書設計研究[J].通信技術,2009,42(02):171-173.