大跨度連續剛構橋的彈塑性動力時程分析
劉大明 劉文浩
1 概述
在各國抗震設計規范中,抗震設計的基本原則是“小震不壞,中震可修,大震不倒”。由于交通中斷造成直接、間接經濟損失巨大。且對于許多大型橋梁空間結構來說,采用線性結構分析并不是真實的安全設計[1]。因此,除要進行結構在“小震”作用下的彈性分析外,還要進行“大震”作用下的彈塑性動力反應分析。
本文利用剛度退化三線性模型對某大跨度連續剛構橋實體工程進行了彈塑性動力時程分析,確定了橋墩塑性鉸對結構抗震性能的影響。算例分析結果可為同類橋梁工程的抗震設計提供參考。
2 剛度退化三線性模型彈塑性動力分析
2.1 剛度退化三線性模型
該模型的主要特點是:用三段折線代表正、反向加載恢復力骨架曲線,并考慮鋼筋混凝土結構或構件的剛度退化性質(如圖1所示)。
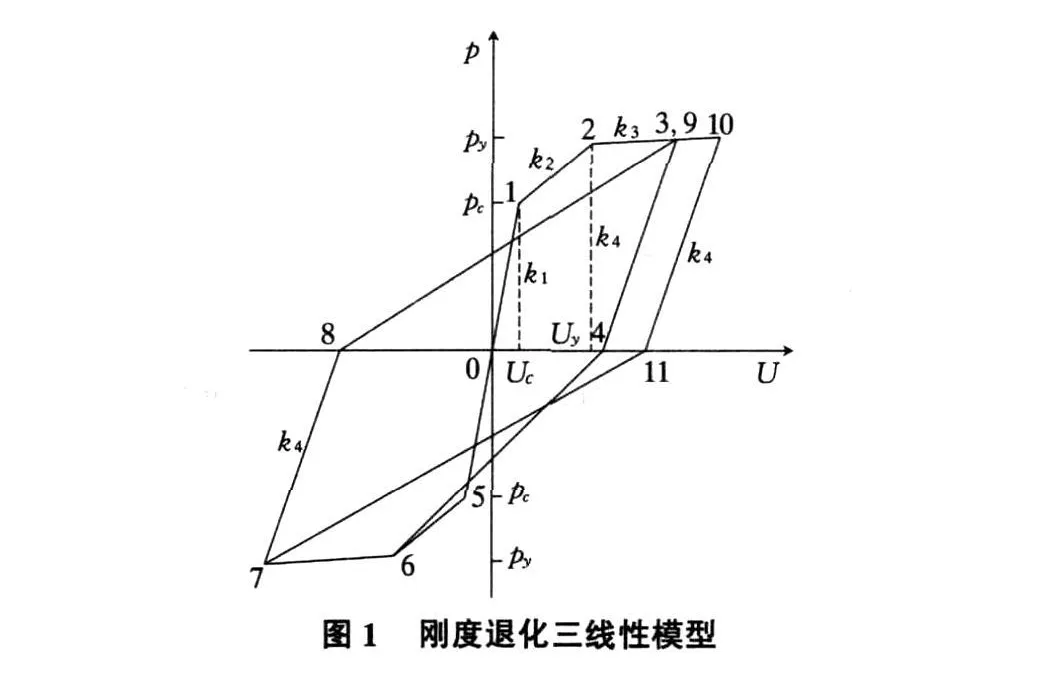
1)三折線的第一段表示線彈性階段,此階段剛度為k1,點1為開裂點。第二段折線表示開裂至屈服的階段,此階段剛度為k2,點2為屈服點。屈服后則由第三段折線代表,其剛度為k3。2)若在開裂至屈服階段卸載,則卸載剛度取k1。若屈服后卸載,則卸載剛度取割線2的剛度 k4。3)中途卸載,卸載剛度取 k4。4)1-2段(2-3段)卸載至零,第一次反向加載時直線指向反向開裂點(屈服點)。后續反向加載時直線指向所經歷過的最大位移點。
2.2 剛度退化三線性模型中的特征參數
若已知構件開裂荷載 pc及彈性剛度k1,開裂點(點1)即可確定。屈服點(點2)則可根據構件屈服荷載 py及屈服點割線剛度k4確定。k4表示為:

其中,αy為屈服點割線剛度降低系數。
顯然,若已知 pc,py,k1,αy,即可完全確定模型(如圖1所示)。對鋼筋混凝土梁、柱,pc,py通常取為梁、柱開裂彎矩與屈服彎矩;k1則為梁、柱截面彈性彎曲剛度或梁、柱彈性彎曲剛度[2]。
3 工程實例
3.1 工程概況
大橋設計荷載為公路—Ⅰ級,主橋為75 m+136 m+75 m三跨預應力混凝土變截面連續剛構箱梁橋,全長286 m。全幅橋箱梁采用分離式單箱雙室截面,C50混凝土,頂板寬度為20.25 m,底板寬13.25 m,翼緣寬3.5 m,最大懸臂長69 m,墩頂梁段高為7.5 m,跨中梁段高為 3 m,箱梁頂板厚 0.26 m,邊跨端部現澆段腹板厚度65 cm,其余梁段腹板采用65 cm,55 cm,40 cm三種厚度,中間設過渡梁段,箱梁采用三向預應力體系。
主墩墩身采用單箱雙室的箱形薄壁斷面,墩寬13.25 m,墩厚3 m,壁厚 0.6 m。主墩承臺采用整體式承臺,承臺厚度4 m,橫橋向兩端做成弧形,承臺封底混凝土厚度0.5 m。每個主墩基礎采用12根D250 cm的鉆孔灌注樁,樁基按嵌巖樁設計。橋面鋪裝采用10 cm厚瀝青混凝土。
3.2 橋墩和樁計算模型中特征參數
根據文獻[3]~[5]和上述理論及公式,文中模型做了簡化計算,只以墩柱在初始狀態下的受力來計算模型特征參數,不考慮在地震過程中結構受力狀態改變對模型特征參數的影響,計算結果見表1。
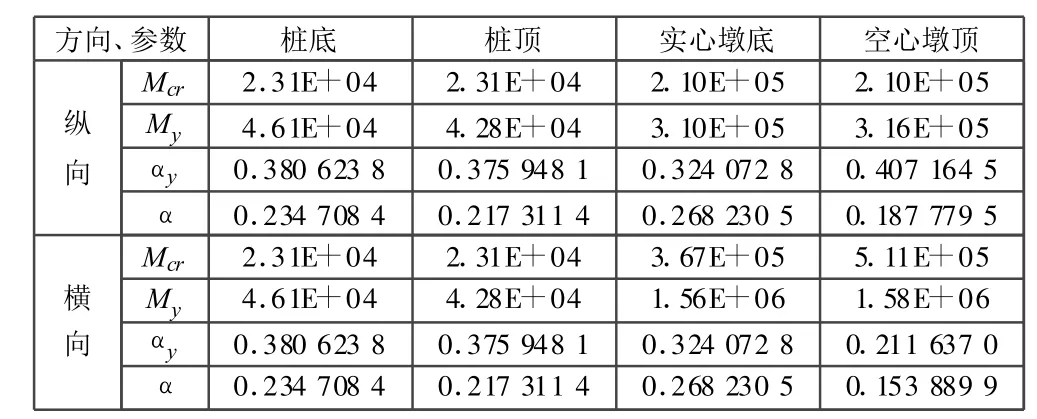
表1 特征參數 kN?m
3.3 彈塑性動力時程分析結果
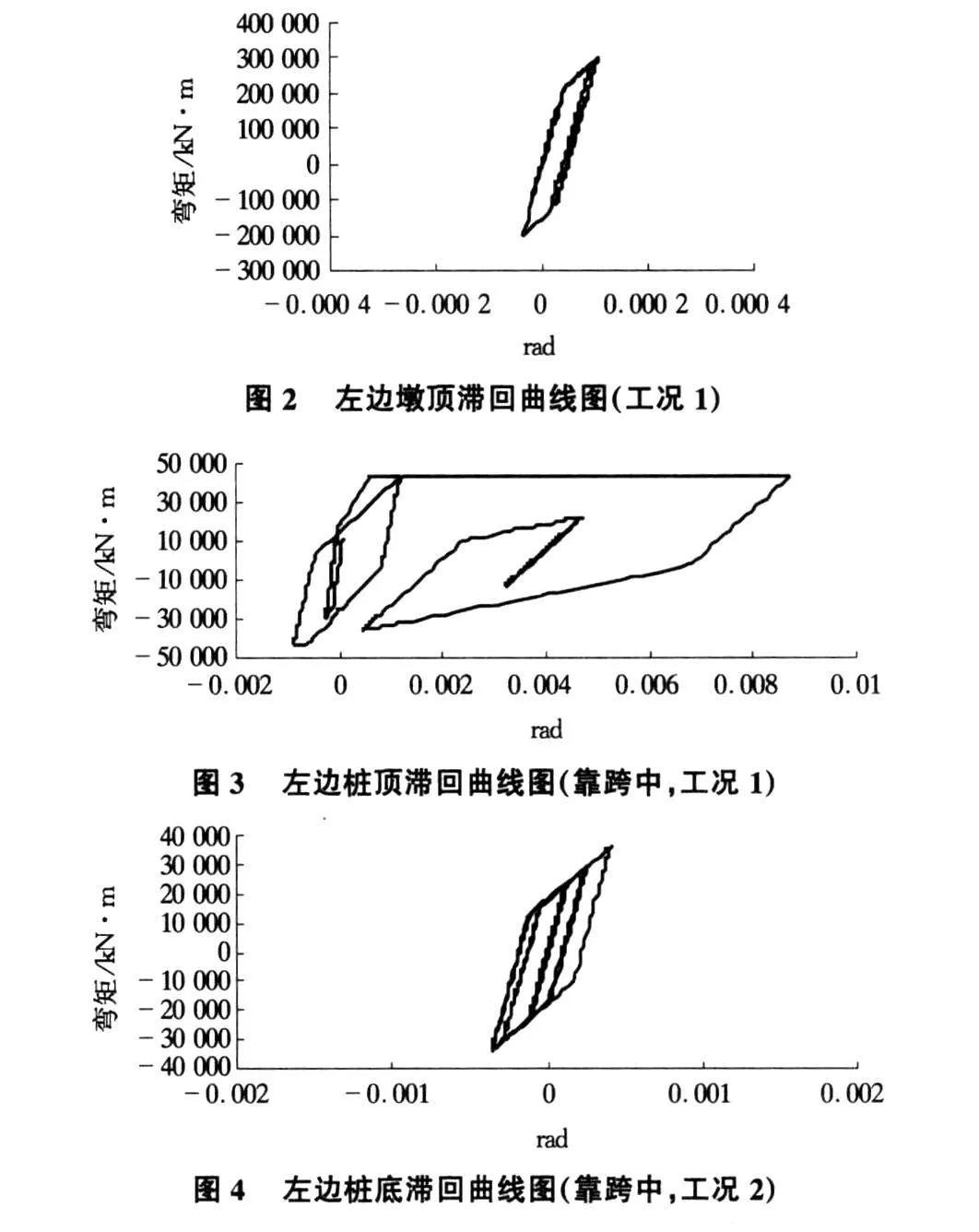
計算模型選取了工況1(自重+縱向地震+0.5豎向)和工況2(自重+橫向地震+0.5豎向)兩種工況,同時為了能夠體現橋梁局部位置的塑性性能,在計算時將地震波峰值加速度調整為0.62g(9度罕遇地震)。計算結果見圖 2~圖4。
從圖2~圖 4可以看出:
1)工況1作用下,墩頂截面滯回曲線為一棱形,但其中并無水平段。表明截面已進入開裂階段但仍未進入屈服階段,圖中棱形所圍成的大小表示截面開裂后所消耗的地震能量。樁頂和樁底的滯回曲線都出現了水平段,表明截面進入屈服階段,塑性鉸變形已十分明顯,表明鉸已進入完全塑性狀態,其中樁頂的塑性鉸變形大于樁底變形。由此可以看出,此橋梁結構的薄弱環節主要是在樁頂,樁底和墩頂截面。
2)工況2作用下,樁頂滯回曲線出現了水平段,表明截面進入屈服階段,但塑性鉸變形比工況1要小,塑性鉸也已進入完全塑性狀態。樁底截面的滯回曲線為一棱形,但其中并無水平段,表明截面已進入開裂階段但仍未進入屈服階段。由此可以看出,此橋梁結構的薄弱環節主要是在樁頂、樁底。鑒于此,作者認為有必要提高樁的自身剛度,同時在樁頂和樁底位置局部加大配筋并且加密箍筋,提高其延性。
4 結語
1)橋梁的塑性鉸是先在樁中出現,此處位于橋梁的下部基礎隱蔽處,由于地震過后橋梁裸露部分的修復和重建比隱蔽的下部基礎更為經濟、省時、省力,因此在設計過程中應盡量使地震時在橋墩而不是在基礎出現塑性鉸,也即要求橋梁基礎的抗震能力應比橋墩高。
2)彈塑性動力時程分析方法考慮結構材料的彈塑性,研究控制破壞程度的條件,進而可以尋找防止結構倒塌的措施。易于工程師在設計中掌握和應用,在今后的橋梁設計中,不失為一種簡單的抗震設計分析方法。
[1] 李光輝.大跨度連續剛構橋空間地震反應分析[D].成都:西南交通大學碩士學位論文,2005.
[2] 張新培.鋼筋混凝土抗震結構非線性分析[M].北京:科學出版社,2003.
[3] 龍曉鴻,李 黎,唐家祥,等.澳凼第三大橋斜拉橋的非線性地震反應及TMD初步控制研究[J].土木工程學報,2004,37(11):56-61.
[4] Fajfar P,Gaspersic P.The N2method:the seismic damage analysis of RC buildings earthquanke[J].Engineering and Structural Dynamics,1996(25):31-46.
[5] 王亞勇.關于設計反應譜、時程法和能量方法的探討[J].建筑結構學報,2000,21(1):21-28.

