三相SPWM逆變電源輸出電壓的諧波抑制綜合方法
王正 潘高強
(沈陽工業大學電氣工程學院,沈陽 110178)
1 引言
隨著SPWM控制技術在電力電子逆變電源的廣泛應用,為了降低逆變電路輸出側產生的高次諧波對其負載和周圍電氣裝置所產生的負面影響,人們把改善輸出波形,消除諧波,提高波形質量作為一項重要的研究內容。所以,對SPWM波形的諧波分析有著十分重要的意義。
針對現代各行各業對電氣設備控制性能日益提高的要求,本文對電壓型SPWM逆變電源的控制方法進行了諧波分析,根據諧波在頻譜上的分布情況,提出減少諧波對電機及其他用電設備危害的方法。
2 SPWM逆變電源模型的建立
正弦脈寬調制(Sinusoid Pulse Width Modulation-SPWM)是在脈寬調制(PWM)的基礎上發展起來的。因其調制波采用正弦波故稱為正弦脈寬調制。正弦波脈寬調制SPWM是利用三角波與正弦波的交點作為逆變電源的開關控制信號,SPWM逆變電源主電路和控制方式波形如圖1所示。其中逆變電源的主回路采用高速開關元件,以保證逆變電源能工作在較高的開關頻率下。SPWM控制技術的實質在于功率開關元件的開關信號是通過期望頻率的正弦調制波與特定的載波信號相比較而獲得的。這種方法適用于各種調頻或調壓裝置中,是一種開關式穩壓電源領域廣泛應用的方法。在變頻器中,通過正弦脈寬調制來控制逆變電源的功率開關器件的導通或關斷,將整流器變換成的直流電壓逆變為具有可控幅值和頻率的電壓源。
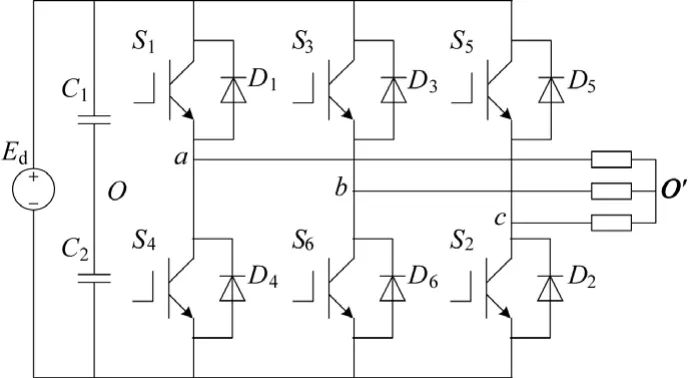
圖1 三相SPWM逆變電源原理圖
3 SPWM逆變電源的諧波分析
3.1 諧波分析的基本假設
為了便于分析諧波,在此對SPWM逆變電源作以下假設.
假設1:支流環節電壓Ed是最理想的電壓源,不考慮其紋波對逆變器輸出的影響;
假設2:視功率開關元件為理想器件,具有理想的開關特性。
3.2 逆變電源輸出電壓的諧波分析[1]
在3.1的假設下,SPWM逆變電源的輸出相電壓傅里葉級數表示為
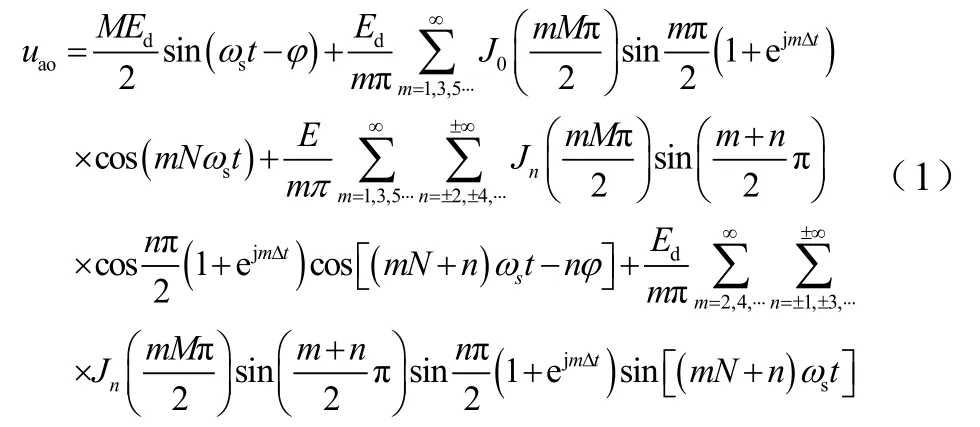
同理可得ubo、uco,所以在不考慮死區Δt的情況下,線電壓uab=uao-ubo,將上式代入并簡化得
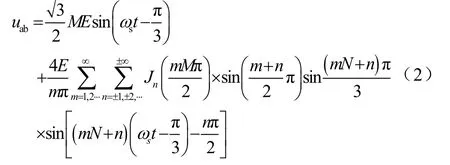
式中,ωs=2πfs;fs為調制波頻率;Ed為直流電源電壓;M為調制度;N為載波比;m為相對于載波的諧波次數;n為相對于調制波的諧波次數;φ為調制波初相; J0,? ??,Jn為第一類Bessel函數。
由式(2)輸出電壓的諧波集中分布在
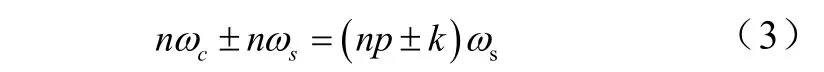
其中,n=1,3,5,…時,k=3(2m-1)±1,m=1,2,3…n=2,4,6…時,k=6m±1,m=0,1,2,…,或k=6m±1,m=0,1,2, …,
由上式可知,在載波頻率的整數倍處的高次諧波不再存在。SPWM 的諧波分布帶有明顯的“集簇”特性,也就是一組一組地集中分布于載波頻率的整數倍頻率兩側,而且在每一組諧波中,隨著k的增大,即遠離該組諧波的中心,則諧波幅值通常逐漸減小。值得考慮的最低次諧波為p-2次。另外,由于3的整數倍次諧波屬諧波分量,故逆變電源輸出線電壓中將不存在3的整數倍次諧波。
4 SPWM逆變電源的諧波抑制
為抑制SPWM電壓源型逆變電源的輸出諧波,從工程實際出發,正確選擇和精確實現載波頻率是使輸出波形改善的最簡潔途徑。但是隨著載波頻率的提高,會增加功率元件的開關次數和開關損耗,提高對功率元件和控制電路的要求。本文將分別從調制法和計算法兩個角度來提出SPWM逆變電源的諧波抑制方法。
4.1 基本的抑制方法[2]
選擇合適的載波頻率,以消除低次和某些奇次諧波。SPWM的載波頻率越高,則逆變器輸出電壓諧波頻率也就越高,所需的濾波器的體積就越小。雖然提高載波頻率可以消除逆變器的低次諧波減小電機的諧波損耗,但是也會使逆變器開關損耗大幅度增加。因此為協調二者的矛盾,一般認為在中小功率的IGBT逆變器中,SPWM的載波頻率取3kHz左右為宜。同時,載波比N應為3的整數倍,以消除3的整數倍數次諧波。
精確實現選定的載波頻率,以避免異步調制中會出現的偶次諧波。但是,在實現選定的載波頻率時,無論采用模擬電路,還是采用數字電路,總是不可避免地帶來一定的誤差。為避免以上情況的出現,需要設法使載波頻率精確實現,盡可能減小載波頻率誤差。在載波頻率誤差不可避免的情況下,可在SPWM的實現中強行使載波和正弦調制波同步。
4.2 調制法
所謂調制法就是在正弦調制波中疊加入一定比例的零序諧波,即3倍頻諧波的諧波注入式SPWM(HIPWM)。它能使調制波呈現出馬鞍形,以降低調制波幅值,增大直流電源電壓的利用率,同時又能使逆變電源具有良好的諧波抑制特性[1,3]。
在正弦函數中注入一定的零序諧波后,其調制函數可表示為
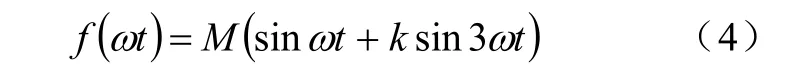
式中,Μ為調制系數;k∈[0,1]為注入的3次諧波的系數。
當k 取不同值時,調制函數 f(ωt )中注入的3次諧波含量亦不同。圖2為調制系數Μ為0.9情況下k 不同時的調制函數波形,其中包括k=0、0.1、0.2、0.5四種情況。
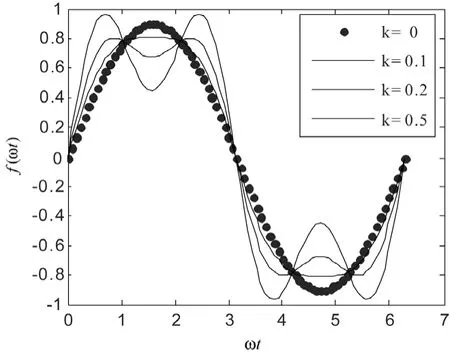
圖2 注入三次諧波后的調制函數波形圖
由圖2可見,改變k便可改變調制函數 f(ωt)與橫軸之間包圍的面積,從而可使逆變器輸出電壓的幅值隨之改變。同時,當逆變電源加入對稱負載時,3的整數倍諧波自行消失,因此,注入3次諧波分量的SPWM并不增加逆變器輸出電壓中的諧波含量。
4.3 計算法
本文介紹在計算法中一種較有代表性的方法——特定諧波消去法。其基本理論是在電壓波形的特定位置設置“缺口”,通過每半個周期間中逆變器的多次換向,恰當地控制逆變器脈寬調制電壓的波形,通過脈寬平均法把逆變器輸出的方波電壓轉換成等效的正弦波,以消除某些特定的諧波。
若以圖1中的直流側電壓中點O為參考點,可得出a相雙極性的電壓輸出波形,如圖3所示。而b、c相的電壓波形只需將a相的波形移相120°和240°即可得到[4-5]。
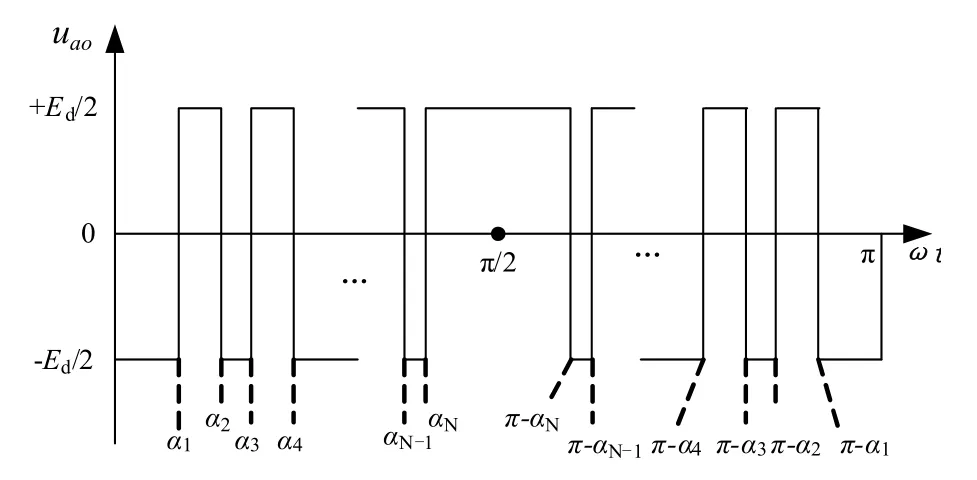
圖3 特定諧波消除PWM的相電壓波形
從0到π /2的電壓波形有N個開關時刻,波形在[0,2π]域對 π 點為中心對稱,在[0,2π ]域對 π/2點為軸對稱,因此,a相電壓的傅里葉級數為
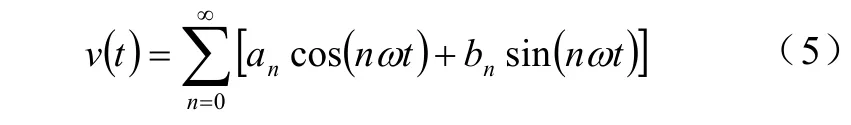
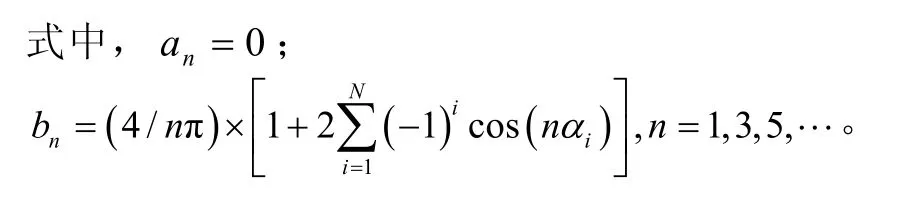
式(5)表明,諧波幅值與開關角α有關,只要適當選擇N個α值,就可以使基波電壓得到控制并且消除N-1個頻率的特定諧波。對于三相對稱負載而言,3的整數倍次諧波在線電壓中因同相被抵消,所以只存在的諧波次數為5,7,11,13,…。
如果令q為選定的輸出基波電壓與逆變器直流側電壓的幅值比[(E1Ed2)],被指定消除的N-1個諧波幅值為零,則周期內的開關角的方程組為
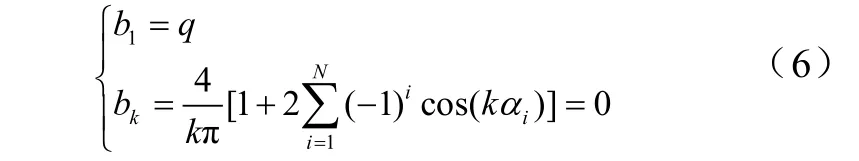
式中,k=6±1(i =1,2,???)為諧波次數;αi為1/4周期內第j個開關角。
5 仿真與試驗驗證
5.1 調制法的仿真驗證
本文就圖1所示電路應用Matlab/Simulink作仿真分析[6]。仿真負載為異步電動機,電動機星形連接,空載運行,逆變器采用雙極性同步調制,載波為共用的等腰三角波,頻率 fc=2850Hz;調制波為三相正弦波,頻率 fs=50Hz,調制度M=0.9。式(4)中k從0到0.5之間變化,得出在不同3次諧波系數k時逆變器輸出電壓諧波含量變化如表1所示。
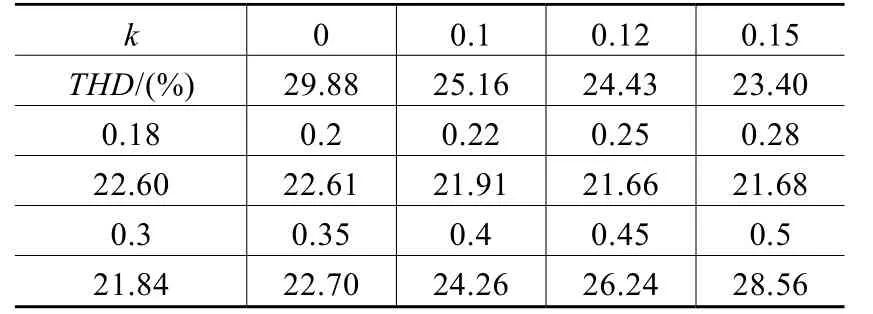
表1 不同k時逆變器輸出線電壓諧波含量變化
由表1可知,當k=0(即沒有注入三次諧波)時,逆變電源輸出線電壓uab的THD為29.88%。
當k由零逐漸增大時,逆變電源輸出線電壓THD就逐漸減小。直到k=0.25時,逆變器輸出線電壓uab的THD為21.66%,此時逆變電源輸出線電壓uab的THD最小。
當k值超過0.25時,逆變器輸出線電壓uab的THD又逐漸增大。當k=0.5時,逆變器輸出線電壓uab的THD為28.56%。由以上分析說明:三次諧波分量的注入并不是越多越好,更不能隨便定一個數值,而是要根據具體的電路結構和載波頻率來選擇一個比較合適的值。本文仿真得到比較理想的k值為0.25。
在某種意義上,可以認為注入3次諧波分量的SPWM逆變器輸出電壓中的諧波含量有所減小,從而在一定程度上改善了逆變器的輸出電壓特性。
5.2 計算法的仿真驗證
同調制法的仿真一樣,本文也利用Matlab對SHE做了仿真驗證。負載為異步電動機,電動機星形連接,空載運行,N=9,fc= 2850Hz,fs= 50Hz,q=0.6,Ed2=190V;實驗步驟包括:利用編制的開關角計算程序,計算出事先設定的q、N值所對應的開關角時刻并生成數據文件。將該數據文件與仿真實驗模型相連,用于控制觸發角。
據式(4)所抑制的諧波次數來看,對于給定的N,能抑制的最大諧波次數為。也就是說,諧波出現的次數應為以上的諧波。本文N=9時,能抑制的最大諧波次數為25,在頻譜圖上就會出現29次以上的諧波。表2為N=9時基波及各次諧波幅值,圖4和圖5為SPWM調制與SHEPWM調制線電壓的頻譜圖。
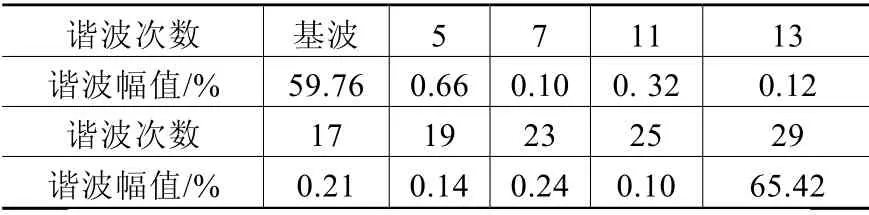
表2 基波及各次諧波幅值
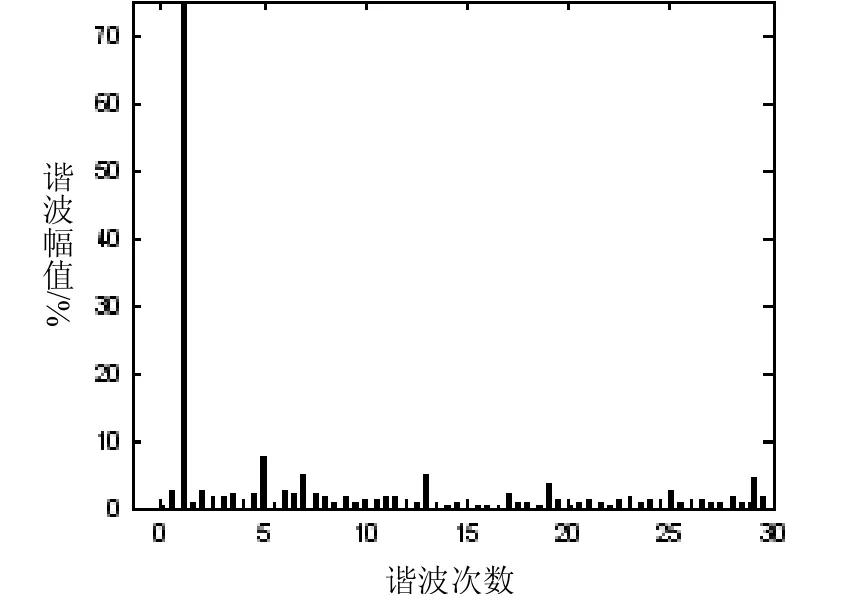
圖4 SPWM線電壓頻譜圖
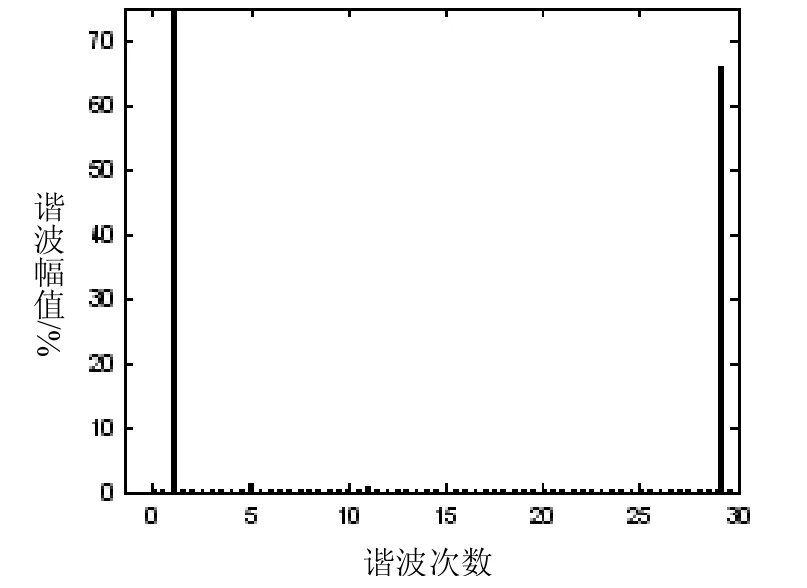
圖5 特定諧波消除PWM線電壓頻譜圖
從仿真結果來看,線電壓的基波幅值與設定的q值一致,5、7、11、…、6i±1次特定諧波得到了有效的抑制;通過對SHEPWM仿真實驗,進一步驗證了用計算出的開關角來控制的逆變電源,能夠實現抑制特定諧波,對SHEPWM技術的實用化具有一定的參考價值。
本文設計出一功率為500W的PWM逆變器。圖6和圖7分別為SPWM調制與SHEPWM時輸出濾波電容上測量得到的波形,對波形進行分析發SHEPWM技術消除諧波的效果要好于SPWM,這與理論和仿真實驗相一致。
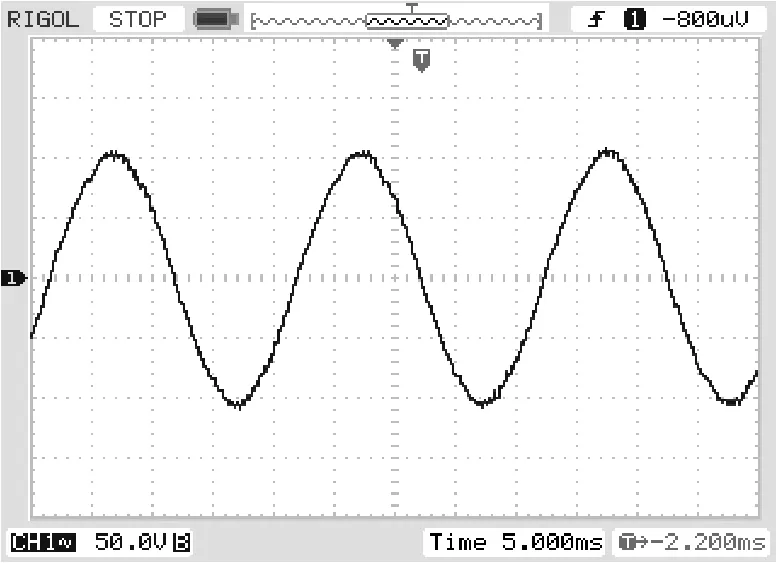
圖6 SPWM調制制輸出波形
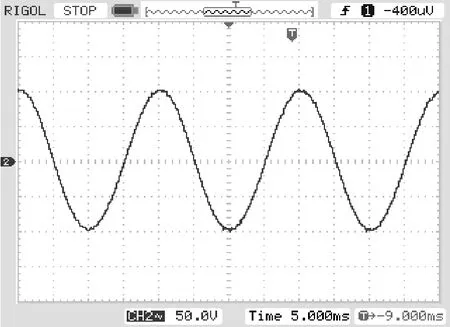
圖7 SHEPWM調制時輸出波形
6 結論
本文主要分析研究了電壓型SPWM逆變器輸出電壓諧波及其產生規律,并通過仿真進行了驗證。從調制法和計算法兩個角度分析研究表明:注入適當的三次諧波分量都應是工程應用上較為有效的諧波抑制方法,而且該種諧波抑制方法比較簡單,在工程上容易實現;采用SHEPWM技術使逆變電源具有優良的諧波抑制特性,能夠從根本上解決諧波抑制問題,隨著DSP等處理芯片的快速發展,通過軟件、硬件的設計可使SHEPWM這一很有前景的技術盡快走向實用化。
[1]劉鳳君.現代逆變技術及應用[M].北京:電子工業出版社, 2006.
[2]吳忠,等.自然采樣SPWM電源的諧波分析及抑制策略[J].電網技術, 2001,25(4): 17-20.
[3]HE Yu-yao,LiHong,HeHua.A novelsoft SPWM waveform synthetic method and harmonic analysis[J].Proceedings of the CSEE,2002,22(12):118-122.
[4]孫柯,羅利文,吳曉毅.利用特定消諧技術進行PWM逆變器的設計[J].儀表技術,2007,5:55-57.
[5]費萬民,呂征宇,姚文熙.多電平逆變器特定諧波消除脈寬調制方法的仿真研究[J].中國電機工程學報,2004, 24(1):102-106.
[6]洪乃剛等編著.電力電子和電力拖動控制系統的Matlab仿真[M].北京:機械工業出版社, 2006.

