一種改進的七電平逆變器對比仿真研究

孫長冬 黃松清 劉緒良 謝玉干 龍佼佼

（安徽工業大學電氣信息學院，安徽 馬鞍山 243002）

1 引言

近年來，多電平結構大量應用于高壓大功率等場合，主要是多電平逆變器由于其電平數多、開關頻率低、輸出諧波小等特點，因此越來越受到重視，并得到迅速發展。到目前為止，各國學者提出了大量的拓撲結構，歸納起來主要有三種：二極管鉗位型、飛躍電容型多電平逆變器、級聯型。

傳統的逆變器由于輸出的PWM脈沖波電平數很少，因此存在很高的電壓變化率和共模電壓，而且波形諧波含量較大，使得輸出濾波器的設計更加復雜。為了解決這些問題，發展了各種多電平逆變器電路。所謂多電平逆變器，就是采用多個直流電源和電力電子器件經過特定的拓撲變換，控制不同的直流電源輸出，將其組合成不同幅值的多電平交流輸出的功率變換裝置。這種逆變器在高壓大容量電力電子系統中發展迅速，成為電力電子領域新的研究熱點。自1980年日本學者A.Nabse提出三電平中點鉗位式逆變電路以來，經過多年的發展，現已形成鉗位型和級聯型兩大類多種樣式的多電平逆變器拓撲結構。豐富了多電平逆變電路的拓撲形式。

本文結合傳統兩電平逆變器和嵌位多電平逆變器的拓撲結構，取長補短，既采用了兩電平電路結構，也吸取三電平鉗位的優點，以及當今非對稱電路拓撲的研究的特性，提出本文所研究的七電平逆變器的拓撲結構，并對分析了電路的工作原理，通過Matlab對其仿真，用簡單的硬件電路驗證了分析和仿真的正確。此電路和三電平逆變器的單相所用的開關管數量相當，鉗位二極管減少，但是電平數增加到七電平。

2 電路拓撲

圖1給出了單相7電平逆變器的電路拓撲和5電平電路拓撲，7電平電路也正是在5電平電路的基礎之上，5電平工作過程見參考文獻[1]，結合鉗位3電平逆變器，才產生的本文的研究電路拓撲，增加2個開關管，電平數也增加2個，控制方法大致相同。本文主要是對7電平逆變器進行分析和研究，左邊的7電平電路拓撲的前邊 Q3，Q4組成的橋是傳統的2電平單相橋，后邊的 Q5，Q6，Q7，Q8橋是鉗位3電平的單向橋，用 Q1，Q2對電源進行控制，通過對此拓撲進行適當的控制，產生期望的7電平。主要是通過控制開關的導通，讓電源疊加，產生7電平。7電平僅僅是將后板橋換成了鉗位3電平的形式，可以再換成鉗位5電平，可以產生11電平。依次類推可知，如果換成鉗位七電平逆變器的半橋可以產生15電平。同樣如果換成理想的鉗位N電平逆變器，可以產生（2N+1）個電平。電平數越高，需要的獨立電源也越多，控制也會變的更加復雜。

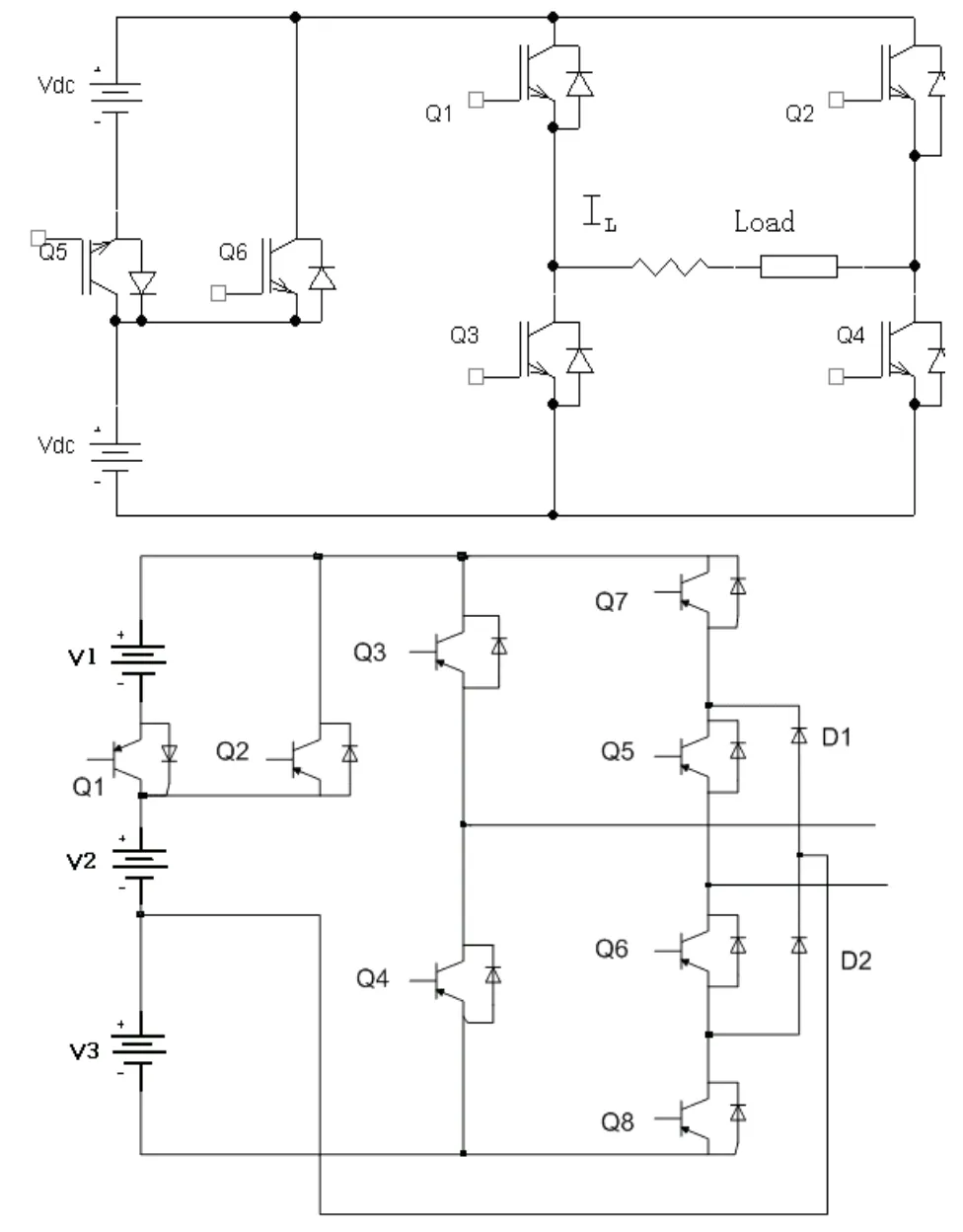
圖1 5電平逆變器電路拓撲和改進的7電平電路拓撲

3 拓撲的工作原理

5電平逆變器的工作原理在此就不再分析，重點分析7電平逆變器的工作原理，圖1有7種工作形式，本文主要對下面這7種工作狀態進行了分析和研究。

（1）第1種工作狀態，令Q3和Q6導通，其余的開關管關閉。電流從電源V2的正極開始，通過Q2的反并聯二極管，以及Q3和Q6，還有嵌位二極管D2形成電流回路，最后流回電源V2的負極。輸出電壓為+V2。

（2）第2種工作狀態，在Q3和Q6導通的基礎上，再令Q8導通，從電源V2的正極開始，通過這三個開關管，流回V3的負極，逆變器輸出電壓為+(V2+V3)。

（3）第3種工作狀態，在以上開關管導通的基礎之上，再打開Q1，電流從電源V1的正極開始通過Q1，Q3，Q6，Q8流回電源V3的負極，逆變器輸出電壓為+(V1+V2+V3)。

（4）第4種工作狀態，令Q2導通，其余的開關管都關閉，電流通過Q2，然后通過Q4，Q5，Q6的反并聯二極管，形成續流回路，此時輸出電壓為0，還有其他的0導通狀態，此處不再分析。

（5）第5種工作狀態，令Q4，Q5導通，其它開關都關閉，電流從V3的正極開始，通過鉗位二極管D1，以及Q4，Q5，最后流回V3的負極。逆變器輸出電壓為-V3。

（6）第6種工作狀態，在第5種工作狀態的基礎之上，再令Q7導通，電流從V2正極開始，經過Q2的反并聯二極管，再通過Q4，Q5，Q7流回電源V3的負極，逆變器輸出電壓為-(V2+V3)。

（7）第7種工作狀態，令Q1，Q4，Q5，Q7導通，其余都關閉，電流從電源V1的正極流出，通過Q1，Q4，Q5，Q7后，流回 V3的負極，逆變器輸出的電壓為-(V1+V2+V3)。

（8）第8種工作狀態，令Q2導通，其余開關管都關閉，形成電流的續流回路，逆變器輸出的電壓為0。

4 電路拓撲的控制原理

一種拓撲結構，必須采用合適的調制方法，才能得到期望的輸出，不同主電路結構的逆變器都對應有一定的調制方法。本文采用SHEPWM，作為該拓撲的調制方式。該方式的思想是通過傅里葉級數分析，得出特定開關角下的傅里葉級數展開式，然后令某些特定的低次諧波為零，從而得到一個反映N個開關角的N個非線性獨立方程，按求解的開關角進行控制，必定不含這些次數的諧波。通常這種方法著眼于低次諧波和低頻次非3倍次諧波。假設V1= V2= V3=E，圖2明顯滿足狄利克雷充分條件，又屬于1/4周期對稱的波形，所以傅里葉級數不存在余弦項和偶數諧波。于是可得

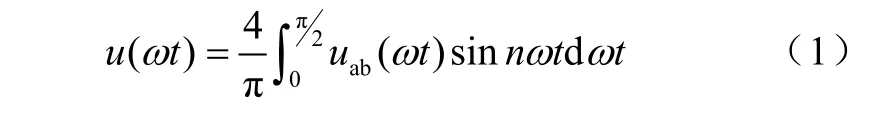
式中，uab是期望輸出的相電壓波形。

將式（1）展開，并解此積分，可得

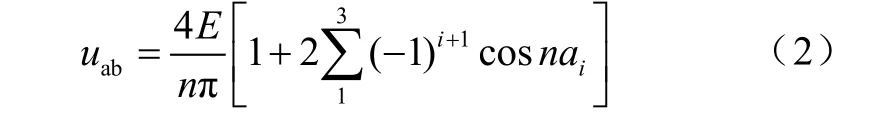
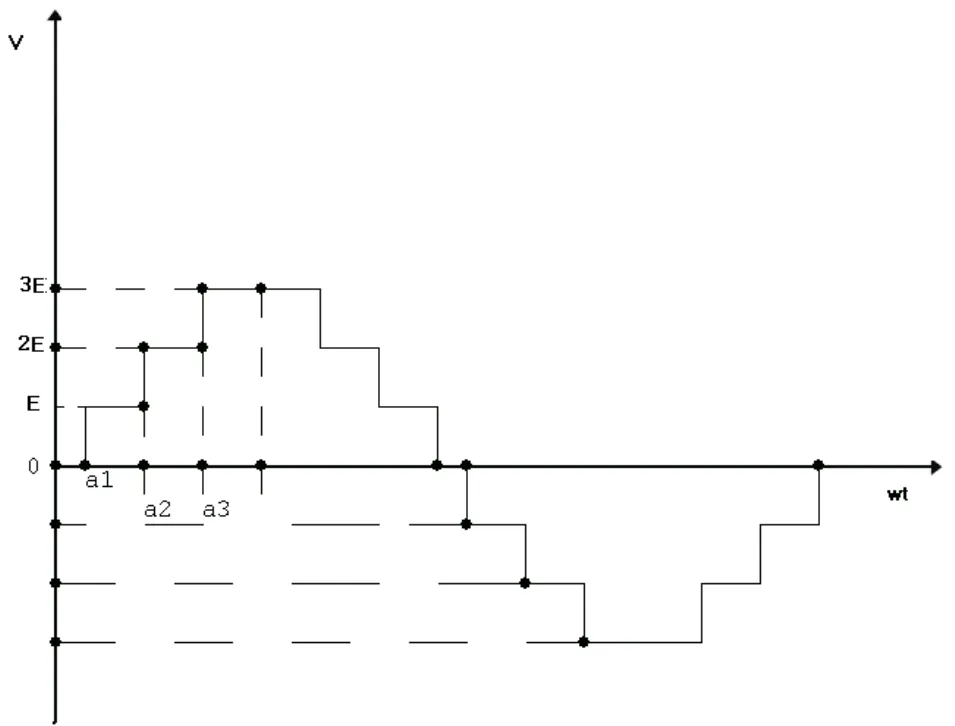
圖2 逆變器輸出電壓波形

令u=(-1)i+1cosnai為調制比，其值的大小決定了直流電壓利用率的大小。由式（2）可列出非線性方程為

根據式（3），并利用牛頓迭代法，即可解出a1、a2、a3的值，從而實現電路的SHEPEM控制。現利用Matlab7.1中的相關數學工具，解出了不同調制比下a1、a2、a3的值。算出角度后，用一個常量代替角度值，與固定周期的正弦波相交，就可以產生相對應的驅動波形。

5 仿真結果

圖3是通過Matlab6.5建立的系統仿真模型，a為5電平逆變器的仿真模型，b為7電平逆變器的仿真模型，每個直流電源的電壓為100V，5電平逆變器的最大直流電壓為400V而7電平逆變器的直流最大電壓為300V，設置頻率為50Hz，仿真結果如圖4。取了前0.1s的輸出波形。拓撲電路的驅動的搭建比較復雜，基本原理就是用正弦波和計算出來的具體角度值的差值，產生驅動。從輸出的仿真實驗結果可以看出，7電平逆變器的波形更加近似正弦波。能夠按照預期的控制方法輸出波形。

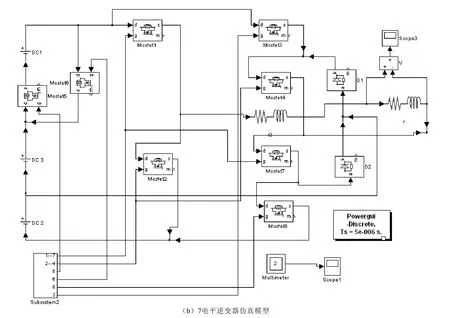
圖3

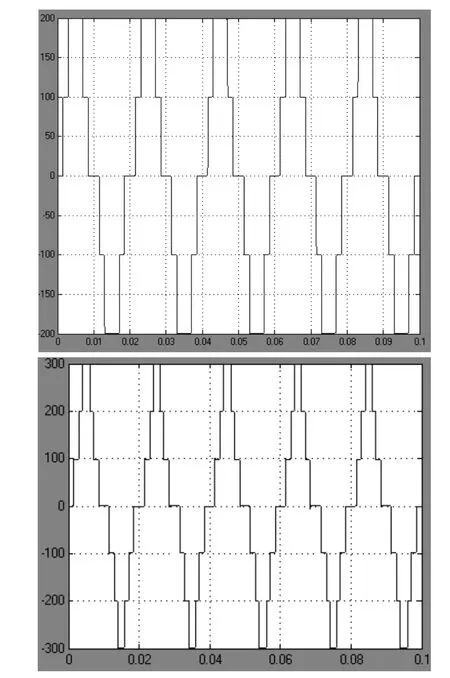
圖4 逆變器輸出電壓波形

6 結論

改電路是對原有的五電平逆變器電路拓撲的改進，控制思路簡單，產生的電平數高，通過了軟件仿真設計和單相電路的研究，三相電路的控制還在進一步的研究，實驗結果表明，這種電路能夠在控制合理的條件下正常工作，且輸出穩定。應用于大功率場合更能體現多電平的好處。

[1]MiroMilanovic,Franc Mihalic and Drago Dolinar.“Component Minimized Topology of DC to three-phase Inverter. World Scientific Publishing Company. 2004,13(4):863–875.

[2]李永東.大容量多電平逆變器-原理、控制、應用[M].北京:科技出版社, 2005.

[3]張艷莉,費萬民.三電平逆變器SHEPWM 方法及其應用研究[J].電工技術學報,2004,19(1):17-19.

[4]王兆安,黃俊.電力電子技術(第4版) [M].北京：機械工業出版社,2006.

[5]洪乃剛.電力電子和電力拖動控制系統的MATLAB仿真[M].北京:機械工業出版社,2006.