二級(jí)新型懸臂式擋土墻有限元分析

王景環(huán) 傅紹娟

隨著經(jīng)濟(jì)的發(fā)展,鐵路、公路、水利等工程上支擋結(jié)構(gòu)大量出現(xiàn),對(duì)支擋結(jié)構(gòu)的要求越來越高,綜合考慮的因素也較多,因此在擋墻的發(fā)展方向上,將更多的考慮結(jié)構(gòu)的輕型化、機(jī)械化,充分發(fā)揮建筑材料的強(qiáng)度性能等特點(diǎn),而懸臂(扶壁)式擋墻能滿足以上要求,同時(shí)還能依靠墻后填土來維持穩(wěn)定,適用一定的交替變形,種種特點(diǎn)說明了二級(jí)懸臂式擋墻必然得到更廣泛的發(fā)展。同時(shí),為了進(jìn)一步擴(kuò)大這種支擋結(jié)構(gòu)應(yīng)用范圍,本文將探討二級(jí)新型懸臂式擋墻這一新形式,為今后的實(shí)際工程提供一定的理論基礎(chǔ)。

1 計(jì)算模型選用

采用平面應(yīng)變的有限元進(jìn)行分析,同時(shí)考慮擋墻與土之間的接觸,在擋墻實(shí)際墻背與填土之間設(shè)置接觸對(duì),選用單元類型的原則是:用最少數(shù)目的單元達(dá)到最高的計(jì)算精度且使運(yùn)算時(shí)間最少,本分析中采用4節(jié)點(diǎn)四邊形等參數(shù)單元將分析范圍進(jìn)行有限元剖分。懸臂式擋墻模型底面長(zhǎng)度為40 m,約為擋墻墻底板長(zhǎng)度的10倍,不考慮擋墻墻踵前土的作用,墻前距離為9 m,墻頂及填土的總長(zhǎng)為31 m,在劃分網(wǎng)格時(shí)采用映射網(wǎng)格劃分方法,在可能的填土范圍網(wǎng)格進(jìn)行加密處理;二級(jí)懸臂式擋墻模型大致同懸臂式擋墻模型,在擋墻計(jì)算墻面內(nèi)加密網(wǎng)格。本文采用ADINA在計(jì)算時(shí)所用的是平面4節(jié)點(diǎn)等參數(shù)單元和Gauss積分方式[1]。

2 計(jì)算參數(shù)

擋墻實(shí)際墻背與填土之間的摩擦系數(shù)為0.3,其他參數(shù)見表1,計(jì)算簡(jiǎn)圖見圖1。

3 邊界條件

二級(jí)懸臂式擋墻有限元網(wǎng)格邊界約束條件:頂部表面自由;兩側(cè)邊界水平約束;底邊界豎向均約束。

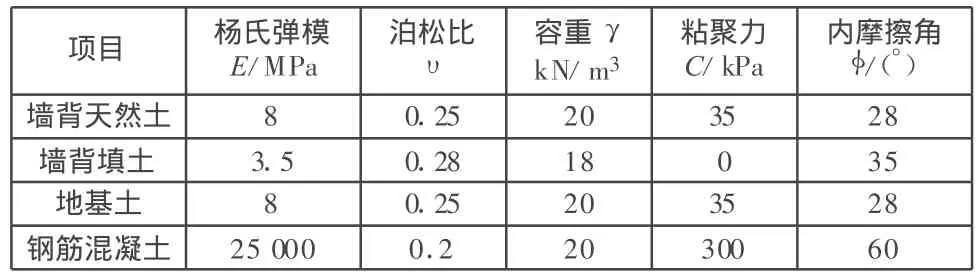
表1 計(jì)算參數(shù)

4 有限元結(jié)果分析

1)實(shí)際墻背位移。從上墻立板水平位移中可以看出,上墻墻頂?shù)乃轿灰戚^大,達(dá)到0.7 mm,朝填土方向移動(dòng),而墻底水平位移則較小,基本上反映了上墻水平位移的線性變化,結(jié)合底板的豎向位移,可以明顯的看出,上墻是繞墻底某點(diǎn)發(fā)生了轉(zhuǎn)動(dòng)并同時(shí)伴隨著擋墻的下沉。在底板的位移圖中,墻趾端處沉降小,而墻踵端處沉降相對(duì)較大,反映出作用在擋墻底板的豎向應(yīng)力的不均衡性,擋墻的平均豎向位移為-6.5 mm左右。上墻豎向位移比水平位移要大很多,反映出擋墻基底的承載能力對(duì)擋墻位移的影響比較大。下墻的水平位移傾向雖然與上墻類似,但下墻是墻頂水平位移小,而墻底相對(duì)來說位移要大一些,而且方向是背離填土方向移動(dòng)的,反映出下墻與上墻不同的位移方式,結(jié)合豎向位移來說,下墻是繞墻頂某點(diǎn)轉(zhuǎn)動(dòng)并伴隨豎向沉降,豎向沉降趨勢(shì)同上墻類似,墻趾位移小,而墻踵端較大。

2)實(shí)際墻背和整體作用下計(jì)算墻面水平應(yīng)力。從水平應(yīng)力云圖中可以發(fā)現(xiàn):上墻墻底板內(nèi)、下墻墻踵板內(nèi)產(chǎn)生了較大正應(yīng)力,應(yīng)該是摩擦所致,在上墻墻趾與立板交接處產(chǎn)生了較大的壓應(yīng)力,在二級(jí)擋墻后的水平應(yīng)力分布較均勻,下墻墻趾處土體中應(yīng)力相對(duì)較大。從實(shí)際墻背即上下墻立板處應(yīng)力圖可以看出,同是類似于三角形的土壓力[3]分布,上墻在0.75 m處應(yīng)力發(fā)生轉(zhuǎn)折,隨后隨墻高的增加而減小;下墻也在0.75 m處應(yīng)力發(fā)生轉(zhuǎn)折,隨后隨墻高的增加而減小,在2.25 m處有個(gè)極值點(diǎn)。

從立板的應(yīng)力圖可以看出,上墻立板的土壓力為13.9 kN/m,解析計(jì)算結(jié)果為9.68 kN/m;下墻立板土壓力為37.5 kN/m,解析計(jì)算結(jié)果為33.725 kN/m;從對(duì)比結(jié)果中可以看出,有限元計(jì)算結(jié)果同解析計(jì)算結(jié)果比較接近,說明上下墻的局部簡(jiǎn)化計(jì)算有一定的合理性。

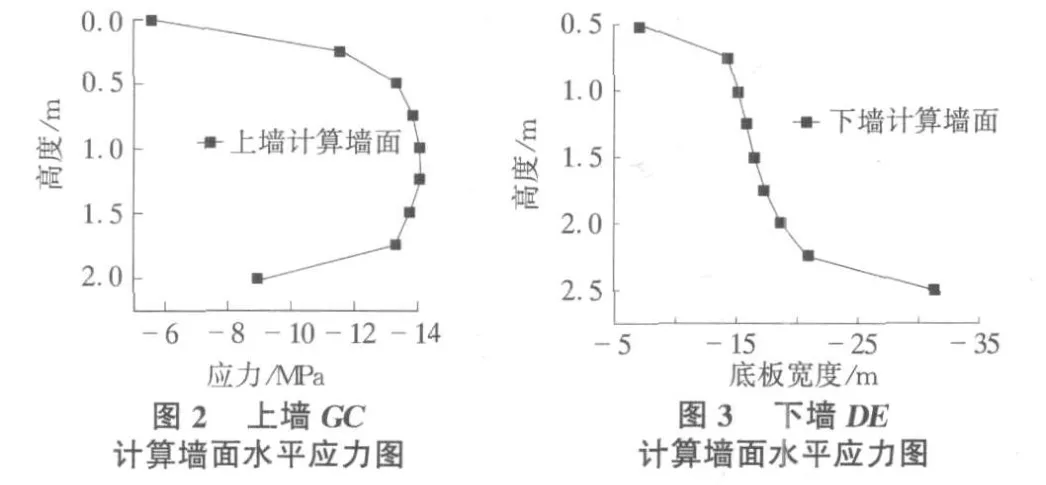
從圖2,圖3中可以看出,作用在上下墻計(jì)算墻面的應(yīng)力分布有明顯的區(qū)別,上墻計(jì)算墻面應(yīng)力0.5 m處以上隨墻高增加而增加,在0.5 m～1.75 m處應(yīng)力呈拋物線分布,在2 m處應(yīng)力又變小,整體形態(tài)上類似于拋物線分布;而下墻計(jì)算墻面有明顯梯形分布特點(diǎn),下墻計(jì)算墻面頂點(diǎn)處有一定的應(yīng)力作用,很明顯是上墻墻底應(yīng)力傳遞所致,下墻計(jì)算墻面最大應(yīng)力發(fā)生在底部,而同下墻立板底部處應(yīng)力比較得知:下墻計(jì)算墻面與下墻立板之間應(yīng)力相差較大,也就是說,下墻計(jì)算墻面與下墻立板之間所構(gòu)成的填土在傳遞作用力時(shí)與填土高度成線性變化有一定的區(qū)別。而上墻計(jì)算墻面應(yīng)力與上墻立板應(yīng)力相比并不相差很大,可能是跟擋墻的高度[4]有關(guān)。從應(yīng)力分析中可知,二級(jí)擋墻上墻同單級(jí)擋墻的分析模式區(qū)別不大,而下墻在做局部分析的時(shí)候可以采用簡(jiǎn)化的解析計(jì)算方法[5]。

3)強(qiáng)度發(fā)揮系數(shù)等值線。從圖4中可以看出墻后填土基本上都處于彈性狀態(tài),在上下墻實(shí)際墻背范圍,填土的強(qiáng)度發(fā)揮系數(shù)變化范圍較大,在靠近上墻墻頂處,強(qiáng)度發(fā)揮系數(shù)從等值線上可以看出將近0.7,下墻強(qiáng)度發(fā)揮系數(shù)最大的地方也在靠近墻頂處,即0.6 m處左右,與實(shí)際墻背上的土應(yīng)力分布有些類似,應(yīng)該是此處土應(yīng)力較大所致,而且在靠近下墻底部處,強(qiáng)度發(fā)揮系數(shù)變化也較大;從圖4中也可以看到,上墻墻底土的強(qiáng)度發(fā)揮比較均勻,而下墻相對(duì)來說要變化大一些,在墻趾處有較大的強(qiáng)度發(fā)揮,可能的原因是下墻除了需承受土的自重以外,還需承受上墻傳遞下來的部分土壓力作用。

5 結(jié)語

1)二級(jí)懸臂式擋墻上墻應(yīng)力分布,跟擋墻的高度、剛度和位移有關(guān),具體相關(guān)性有待進(jìn)一步的考慮,而下墻立板的應(yīng)力類似一般三角形分布,但墻頂處是有相對(duì)較大的應(yīng)力作用的,在以后的設(shè)計(jì)中可以采用本文簡(jiǎn)化的計(jì)算方法得到下墻立板的土壓力分布。2)二級(jí)懸臂式擋墻上下墻計(jì)算墻面的土壓力分布有比較大的區(qū)別,上墻計(jì)算墻面應(yīng)力分布呈拋物線形狀,而下墻更加接近梯形分布,同下墻立板應(yīng)力區(qū)別較大,在設(shè)計(jì)二級(jí)懸臂式擋墻的時(shí)候考慮整體與局部的土壓力作用是很有必要的。3)在本例中,從有限元計(jì)算結(jié)果來看,其土壓力值比解析計(jì)算中的土壓力值要小,而且呈現(xiàn)出非線性變化的特點(diǎn),計(jì)算表明:墻體位移和土壓力要受到墻體剛度、墻背粗糙程度、填土彈模等因素的影響,其中在填土一定的情況下,與墻體剛度最為密切。4)從有限元分析結(jié)果來看,二級(jí)擋墻上墻的卸荷作用比較明顯,與解析計(jì)算結(jié)論相符合,與國(guó)內(nèi)目前已經(jīng)采用的倒F形擋墻卸荷作用類似,同時(shí)土的自重在二級(jí)擋墻中得到了充分的利用,因此在工程運(yùn)用中需保證填土的壓實(shí)度,尤其是上下墻過渡區(qū)域。5)從解析計(jì)算和有限元比較結(jié)果來看,二級(jí)懸臂式擋墻采用類似于有減壓平臺(tái)的擋土墻土壓力計(jì)算方法,與有限元結(jié)果并無太大出入,吻合較好,在今后可能的二級(jí)懸臂式擋墻實(shí)際工程中,可以采用這種方法進(jìn)行土壓力的計(jì)算以作參考。

[1]謝康和,周 健.巖土工程有限元理論與應(yīng)用[M].北京:科學(xué)出版社,2002.

[2]顧慰慈.擋土墻土壓力計(jì)算[M].北京:中國(guó)建材工業(yè)出版社,2001.

[3]錢家歡,殷宗澤.土工原理與計(jì)算[M].北京:中國(guó)水利水電出版社,1996.

[4]張儀萍.沉降的灰色預(yù)測(cè)[J].工業(yè)建筑,1999,29(4):45-48.

[5]鮑爾斯.土力學(xué)計(jì)算[M].北京:人民交通出版社,1982.

[6]Bakeer,R.M.,Bhatia,S.K..Earth pressure behind a gravity retaining Wal.l Int.J.Numer.Ana.l Methods in Geomech,1989(13):665-673.