平翅片表面流動(dòng)和換熱的數(shù)值模擬研究
梁斯麒
近年來(lái),對(duì)制冷換熱器用翅片形式的研究取得了一定的進(jìn)展,文獻(xiàn)[1]研究了多種表面變形片的強(qiáng)化傳熱特征,并根據(jù)單片矩形翅片表面的換熱系數(shù)分布[2],提出在翅片上換熱性能的薄弱區(qū)域開大直徑圓孔,從而改善翅片的換熱效果[3]。但文獻(xiàn)[2]對(duì)局部換熱系數(shù)分布的研究?jī)H局限于單片矩形翅片,與翅片管的實(shí)際情況有明顯差異。蘇華[3]和范亞明[4]等人通過(guò)正交優(yōu)化實(shí)驗(yàn),獲得了2種優(yōu)化片型,即沿管開對(duì)稱大直徑圓孔翅片以及雙側(cè)開非對(duì)稱大直徑圓孔—半圓孔交叉翅片,實(shí)驗(yàn)表明:在最窄截面風(fēng)速Umax=1 m/s~8 m/s的范圍內(nèi),雙側(cè)穿孔方案中最優(yōu)片型的風(fēng)側(cè)當(dāng)量換熱系數(shù) h0比平翅片增加了22.6%~30.4%,平均增幅達(dá)29.5%,ΔP最大增幅不超過(guò)8%;雙側(cè)開非對(duì)稱圓孔—半圓孔的交叉翅片方案中最優(yōu)片型的 h0比平翅片增加了14.3%~20.9%,平均增幅達(dá)18.7%,ΔP最大增幅不超過(guò)6%。高建衛(wèi)等[5]利用家用冰箱制冷系統(tǒng),分別采用圓孔—半圓孔交叉優(yōu)化翅片、圓孔優(yōu)化翅片以及平翅片管式制冷換熱器,進(jìn)行積霜工況下的傳熱和制冷性能對(duì)比性實(shí)驗(yàn)研究。結(jié)果表明:與平翅片相比,當(dāng)最窄截面風(fēng)速為0.5 m/s時(shí),積霜工況下圓孔翅片的傳熱性能最好,其傳熱系數(shù)平均提高了11.53%;對(duì)流換熱系數(shù)平均提高了18.84%;制冷系數(shù)平均提高了6.83%;有效制冷量平均提高了602%,節(jié)省電能6.39%,且積霜工況下圓孔不易堵塞,可在較長(zhǎng)時(shí)間內(nèi)維持較好的強(qiáng)化傳熱特征。根據(jù)文獻(xiàn)[4]矩形翅片管實(shí)驗(yàn)試件的結(jié)構(gòu)建立數(shù)學(xué)模型,運(yùn)用數(shù)值模擬的方法,耦合分析求解出翅片表面的速度分布、溫度分布和努謝爾特?cái)?shù)分布,模擬結(jié)果與文獻(xiàn)[4]實(shí)驗(yàn)數(shù)據(jù)進(jìn)行了比較,證實(shí)了模擬結(jié)果的正確性。
1 模擬計(jì)算模型
1.1 幾何模型
單排管平翅片管式換熱器實(shí)驗(yàn)樣件的尺寸如下:管子外徑D0=25 mm,翅片厚度δ=0.5 mm,管間距 Y=76 mm,翅片間距S=10 mm,翅片寬度 W=61 mm,如圖1所示。
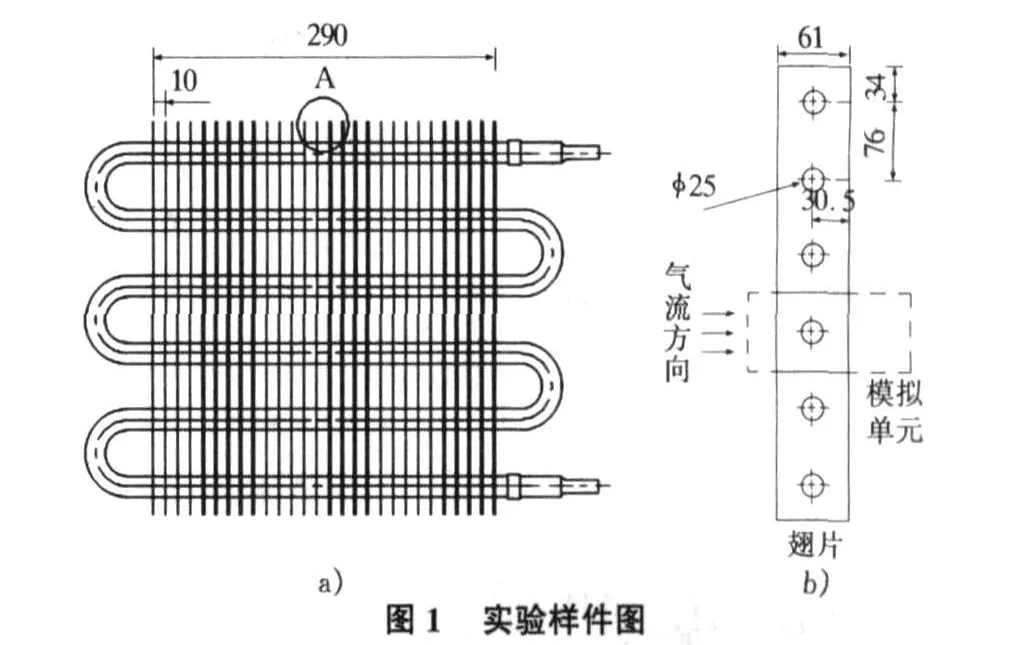
由于結(jié)構(gòu)的對(duì)稱性,模擬計(jì)算時(shí)取樣件其中一個(gè)單元作為模型。為保證空氣無(wú)入口效應(yīng)和出口無(wú)回流現(xiàn)象,入口延長(zhǎng)了1倍管外徑,出口延長(zhǎng)4倍管外徑(如圖1b)中虛線所示)。本文利用Fluent軟件的Gambit模塊,對(duì)模型采用分塊網(wǎng)格劃分的方法進(jìn)行離散,對(duì)某些規(guī)則的區(qū)域采用六面體網(wǎng)格以減少網(wǎng)格數(shù)目,對(duì)一些不規(guī)則區(qū)域采用四面體網(wǎng)格,對(duì)重點(diǎn)研究的區(qū)域采用了加密網(wǎng)格,進(jìn)出口附近采用粗網(wǎng)格。通過(guò)采用不同的網(wǎng)格劃分檢驗(yàn)了網(wǎng)格無(wú)關(guān)性,最后得到總的網(wǎng)格單元數(shù)為15多萬(wàn)個(gè)。
1.2 邊界條件
1)忽略翅片和鋼管的接觸熱阻和翅片與基管間的輻射換熱,翅片根部及鋼管的表面溫度 Tf=347.36 K,翅片表面溫度分布采用翅片導(dǎo)熱、翅片表面與空氣間的對(duì)流換熱耦合求解;2)空氣進(jìn)入換熱器的溫度為297.8 K;3)翅片的導(dǎo)熱系數(shù)為常數(shù);4)對(duì)翅片邊緣及中剖面采用絕熱邊界條件,對(duì)于空氣流道取為對(duì)稱邊界條件;5)翅片及圓管材料為鋼材。
本文采用Fluent6.0軟件計(jì)算,計(jì)算模型采用標(biāo)準(zhǔn) k—ε兩方程模型,各方程的離散化均采用二階迎風(fēng)格式,同時(shí)用Simple[6]算法求解上述控制方程的離散方程組,將能量方程與動(dòng)量方程進(jìn)行耦合求解。
2 計(jì)算結(jié)果及分析
2.1 翅片間中心面的速度分布
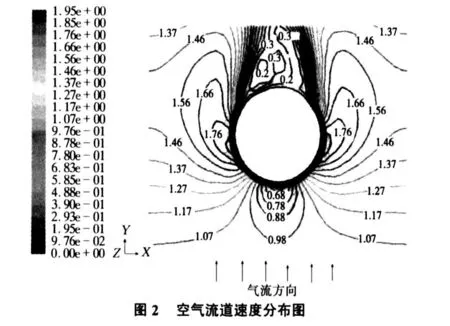
圖2是風(fēng)速 u=1 m/s時(shí)翅片間中心面的空氣速度分布圖,空氣在進(jìn)入流道時(shí)速度分布比較均勻,但由于圓管的阻擋,正對(duì)著圓管的空氣速度逐漸減小,圓管兩側(cè)的空氣速度不斷增大,最大值出現(xiàn)在圓管兩側(cè)的中心部位。靠近圓管的尾部出現(xiàn)分離流動(dòng),形成明顯的渦旋。圓管后面空氣速度很小,形成一循環(huán)流動(dòng)的尾流區(qū)。
2.2 翅片表面溫度分布特征
翅片前沿部分的溫度較低,越靠近圓管,翅片的溫度越高,同時(shí)圓管后面形成一面積較大的高溫區(qū)域,這就是空氣渦旋循環(huán)流動(dòng)的尾流區(qū)。循環(huán)流動(dòng)的空氣不能有效地帶走熱量,使得圓管后面的翅片表面溫度較高,顯然,尾流區(qū)是換熱的薄弱區(qū)域。
2.3 翅片表面換熱特征
在翅片的進(jìn)口段出現(xiàn)了最高的努謝爾特?cái)?shù)。沿著流動(dòng)方向,Nu逐漸減小,這是由于邊界層逐漸增厚導(dǎo)致?lián)Q熱效果降低的原因。Nu數(shù)最小值出現(xiàn)在管后尾流區(qū),這是由溫度分布的特征確定的。在尾流區(qū),空氣不能有效地帶走熱量,換熱溫差最大,因此換熱效果最差,Nu數(shù)最小。采用開孔措施強(qiáng)化傳熱時(shí),管前翅片表面開圓孔可以破壞流動(dòng)邊界層,管后尾流區(qū)開圓孔可以增強(qiáng)氣流擾動(dòng),均可達(dá)到強(qiáng)化傳熱的效果[6]。
3 計(jì)算結(jié)果與實(shí)驗(yàn)結(jié)果比較
為驗(yàn)證模擬結(jié)果的正確性,本文將模擬結(jié)果與實(shí)驗(yàn)結(jié)果進(jìn)行了比較,實(shí)驗(yàn)結(jié)果引自于參考文獻(xiàn)[3]。實(shí)驗(yàn)是在一吸風(fēng)式直流風(fēng)洞中進(jìn)行的,翅片管管內(nèi)采用電加熱,空氣外掠翅片側(cè)流動(dòng)并被加熱。由實(shí)驗(yàn)數(shù)據(jù)整理獲得的對(duì)流換熱系數(shù)與速度的關(guān)系見表1,其中,空氣側(cè)當(dāng)量對(duì)流換熱系數(shù) h0與平均對(duì)流換熱系數(shù)h′0的關(guān)系如下。其中,A0,1為光管對(duì)流換熱面積,m2;A0,2為翅片表面積,m2;A0為總換熱面積,m2;三者之間的關(guān)系為:A0=A0,1+A0,2;ηf為翅片效率。本文進(jìn)行了風(fēng)速分別為1 m/s~4 m/s的數(shù)值模擬,由模擬結(jié)果與實(shí)驗(yàn)結(jié)果的對(duì)比可以看出,換熱系數(shù)隨風(fēng)速的變化趨勢(shì)是相同的,但實(shí)驗(yàn)結(jié)果均小于模擬結(jié)果,兩者比較,最大相對(duì)誤差為10.8%,而最小相對(duì)誤差僅為7.3%。引起誤差的主要原因是模擬時(shí)所用模型為標(biāo)準(zhǔn)k—ε的湍流模型,該模型主要適用于高雷諾數(shù)下充分發(fā)展的湍流流動(dòng)與換熱,與實(shí)際情況有些差別。

表1 不同速度換熱系數(shù)
4 結(jié)語(yǔ)
在現(xiàn)有實(shí)驗(yàn)成果的基礎(chǔ)上,利用Fluent軟件建立矩形翅片管式換熱器單元內(nèi)三維流動(dòng)的數(shù)學(xué)物理模型,并進(jìn)行了相應(yīng)的數(shù)值模擬計(jì)算。計(jì)算結(jié)果與實(shí)驗(yàn)結(jié)果的相對(duì)誤差不大,充分說(shuō)明了數(shù)值模擬的正確性。模擬結(jié)果直觀地顯示了翅片管式換熱器單元內(nèi)的流場(chǎng)結(jié)構(gòu)和換熱特點(diǎn)。模擬結(jié)果表明:空氣外掠翅片管時(shí),管后翅片上的流體發(fā)生分離,形成一循環(huán)流動(dòng)的尾流區(qū),尾流區(qū)內(nèi)流體的循環(huán)流動(dòng)不能帶走熱量,導(dǎo)致溫度升高,換熱效果差。這一區(qū)域是對(duì)流換熱的薄弱區(qū)域。本文的研究為矩形翅片管式換熱器強(qiáng)化傳熱的深入研究提供了理論依據(jù),在換熱薄弱的區(qū)域采取強(qiáng)化傳熱措施將取得事半功倍的強(qiáng)化效果。
[1] 王厚華.外掠單排矩形翅片管的強(qiáng)化換熱實(shí)驗(yàn)研究[J].暖通空調(diào),1995,25(3):34-37.
[2] 王厚華,楊延萍,江 村.單片矩形翅片表面的換熱系數(shù)分布[J].重慶建筑大學(xué)學(xué)報(bào),1998,20(5):57-60.
[3] 蘇 華.擾流孔型翅片管傳熱與流阻性能實(shí)驗(yàn)研究和翅片的數(shù)值計(jì)算[D].重慶:重慶建筑大學(xué)碩士學(xué)位論文,1999.
[4] 范亞明.雙側(cè)開非對(duì)稱圓孔—半圓孔翅片管的傳熱與流阻性能試驗(yàn)研究及翅片效率的數(shù)值計(jì)算[D].重慶:重慶大學(xué)碩士學(xué)位論文,2000.
[5] 王厚華,高建衛(wèi),彭宣偉.圓孔翅片積霜工況下的制冷性能實(shí)驗(yàn)[J].重慶大學(xué)學(xué)報(bào),2007,30(5):4-10.
[6] 陶文銓.數(shù)值傳熱學(xué)[M].西安:西安交通大學(xué)出版社,1998:264-289.

