淺析灰色預(yù)測(cè)模型在建筑工程造價(jià)中的應(yīng)用
李旭方
建筑工程是一個(gè)復(fù)雜的過程,在整個(gè)過程中,工程造價(jià)貫穿始終。工程造價(jià)預(yù)測(cè)是對(duì)一個(gè)計(jì)劃中準(zhǔn)備建設(shè)的工程在實(shí)施前對(duì)其預(yù)期價(jià)格進(jìn)行預(yù)測(cè),是工程項(xiàng)目可行性研究的基礎(chǔ)。
1 灰色預(yù)測(cè)及灰色動(dòng)態(tài)模型
灰色預(yù)測(cè)是灰色理論的重要組成部分。灰色理論是以信息不完全的系統(tǒng)為研究對(duì)象,運(yùn)用特定的方法描述信息不完全的系統(tǒng)并進(jìn)行預(yù)測(cè)、決策、控制的一種嶄新系統(tǒng)理論,是控制論觀點(diǎn)和方法的延伸。灰色系統(tǒng)的實(shí)質(zhì)為:部分信息已知、部分信息未知的一類系統(tǒng)。灰色預(yù)測(cè)是根據(jù)過去的及現(xiàn)在已知的或非確定的信息建立的一個(gè)從過去引申到未來的灰色模型,從而確定系統(tǒng)未來發(fā)展變化的趨勢(shì),并為規(guī)劃、決策提供依據(jù)。
灰色動(dòng)態(tài)模型是灰色系統(tǒng)理論與方法的核心,其特點(diǎn)是生成函數(shù)和灰色微分方程,是以灰色生成函數(shù)概念為基礎(chǔ),以微分?jǐn)M合為核心的建模方法,能根據(jù)少量信息建模和預(yù)測(cè)。灰色建模一般是將原始數(shù)據(jù)先進(jìn)行累加處理,通過這種處理,才能在非負(fù)的時(shí)間數(shù)據(jù)序列中找到某種規(guī)律,然后建立微分方程。灰色系統(tǒng)中常見的模型有狀態(tài)模型、靜態(tài)模型和預(yù)測(cè)模型。
2 灰色預(yù)測(cè)方法在建筑工程造價(jià)預(yù)測(cè)中的應(yīng)用
為了實(shí)現(xiàn)將灰色預(yù)測(cè)理論用建筑工程造價(jià)預(yù)測(cè)中的這一思想,本文根據(jù)近年來某單位框架高層住宅造價(jià)歷史資料,利用灰色理論中的預(yù)測(cè)知識(shí)和GM(1,N),GM(1,L)模型,對(duì)框架高層住宅造價(jià)系統(tǒng)作了以工程總造價(jià)、人工費(fèi)、材料費(fèi)及機(jī)械使用費(fèi)為造價(jià)指標(biāo)的系統(tǒng)預(yù)測(cè)。
2.1 歷史數(shù)據(jù)預(yù)處理
表1是往年框架高層住宅的工程總造價(jià)、人工費(fèi)、材料費(fèi)及機(jī)械使用費(fèi)。
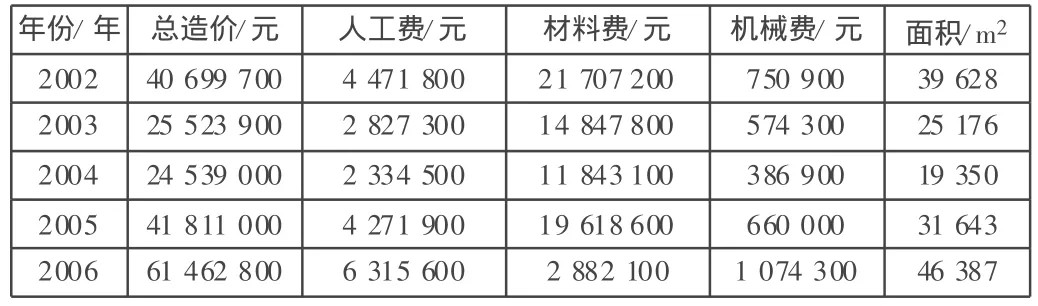
表1 歷史工程造價(jià)數(shù)據(jù)
為了提高模型精度,對(duì)歷史數(shù)據(jù)以2002年數(shù)據(jù)為基準(zhǔn)作初值化處理:
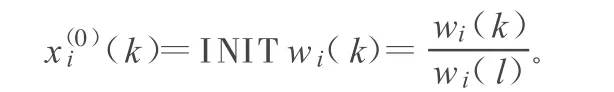
標(biāo)準(zhǔn)化處理后的原始數(shù)據(jù)見表2。
2.2 建模步驟
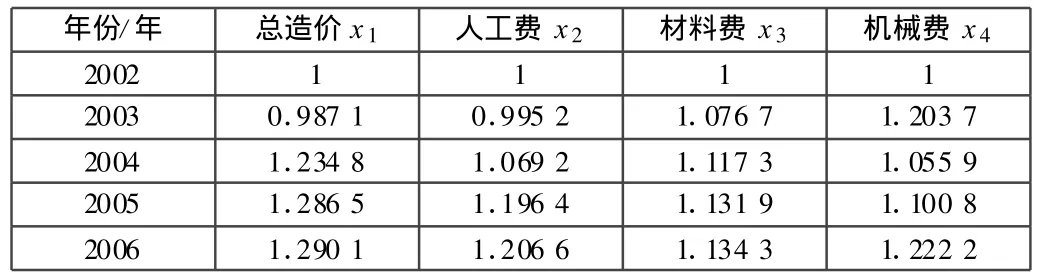
表2 標(biāo)準(zhǔn)化處理后的原始數(shù)據(jù)
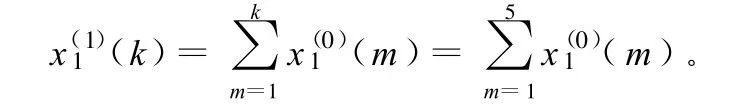
2)根據(jù)下列公式計(jì)算數(shù)據(jù)矩陣B,向量y4。
z(1)=MEANx(1)(MEAN就是將累加生成序列中,前后相鄰數(shù)據(jù)取均值)。
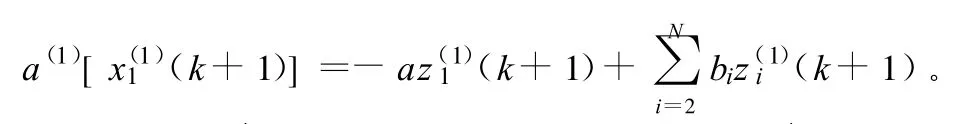
4)建模。根據(jù)前面獲得的參數(shù)a1,b12,b13,b14代入到GM(1,N)模型:
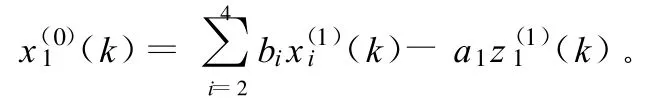
得到模型:
a.工程總造價(jià)x1的GM(1,4)模型:
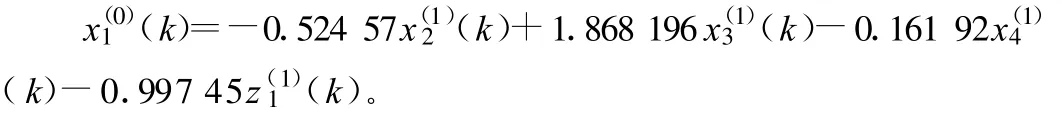
b.人工費(fèi)用x2的GM(1,2)模型:
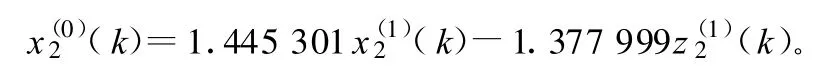
c.工程材料費(fèi)用x3的GM(1,1)模型:
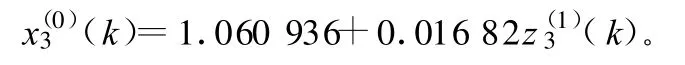
d.機(jī)械使用費(fèi)x4的GM(1,2)模型:
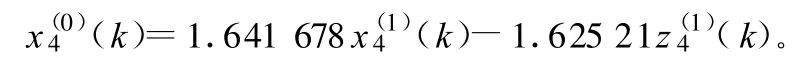
2.3 建立GM(1,N,x(0))模型
為了達(dá)到更好的預(yù)測(cè)效果,以下分別對(duì)工程總造價(jià)x1、工程人工費(fèi)x2、工程材料費(fèi)x3、工程機(jī)械使用費(fèi)x4建立GM(1,N,x(0))模型。GM(1,N,x(0))稱為GM(1,N)的派生型預(yù)測(cè)模型,它由定義型預(yù)測(cè)模型推導(dǎo)出來。
GM(1,N,x(0))模型形式如下:

派生模型中模型識(shí)別參數(shù)α,β的表達(dá)式為:
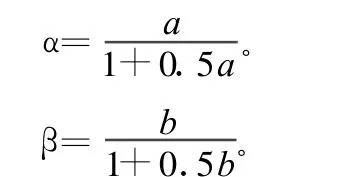
1)工程總造價(jià)x1的GM(1,4,x(0))模型:
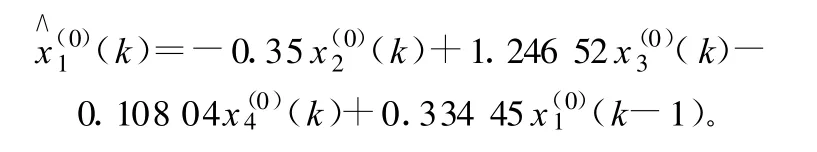
2)人工費(fèi)用x2的GM(1,2,x(0))模型:
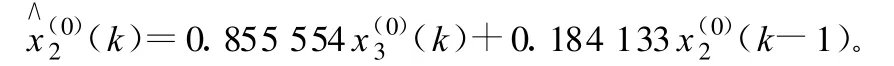
3)工程材料費(fèi)用x3的GM(1,1,x(0))模型:
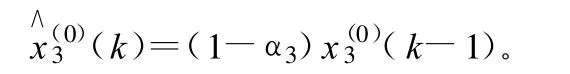
4)機(jī)械使用費(fèi)x4的GM(1,2,x(0))模型:
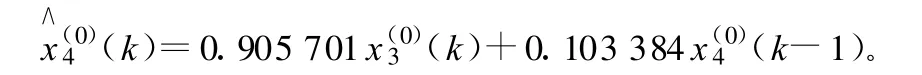
2.4 模型檢驗(yàn)
1)工程總造價(jià)x1的GM(1,4,x(0))模型的精度檢驗(yàn):
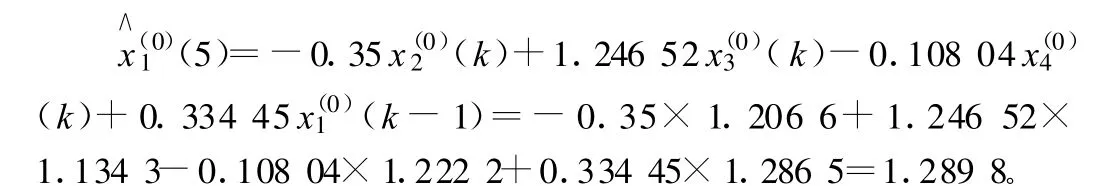
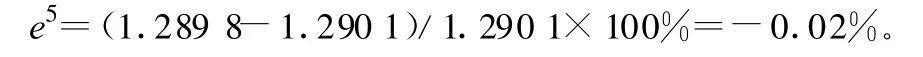
2)人工費(fèi)用x2的GM(1,2,x(0))模型的精度檢驗(yàn):
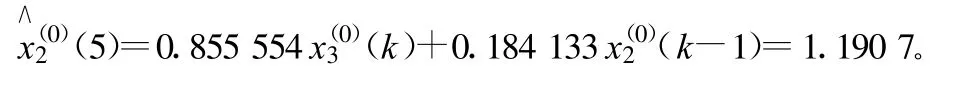
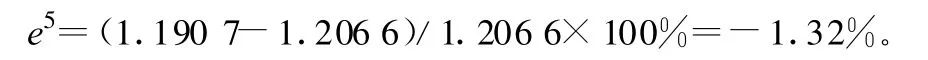
3)工程材料費(fèi)用x3的GM(1,1,x(0))模型的精度檢驗(yàn):
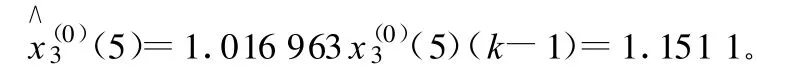
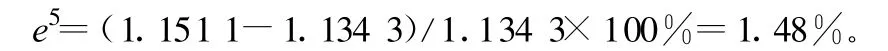
4)機(jī)械使用費(fèi)x4的GM(1,2,x(0))模型的精度檢驗(yàn):
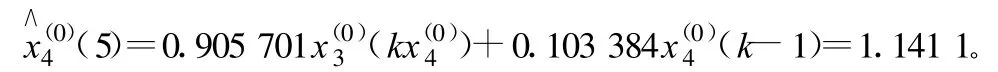
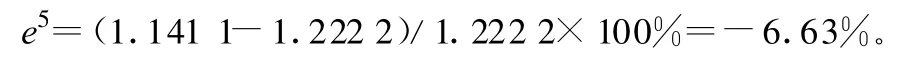
3 結(jié)語
根據(jù)以上模型檢驗(yàn)可知,預(yù)測(cè)值與實(shí)際值有差異,但差異很小,都在容許偏差范圍之內(nèi),不會(huì)影響總體預(yù)測(cè)結(jié)果,完全達(dá)到預(yù)期目的。
[1]鄧聚龍.灰色系統(tǒng)基本方法[M].武漢:華中工學(xué)院出版社,1985:20-75.
[2]劉思峰,郭天榜.灰色系統(tǒng)理論及其應(yīng)用[M].開封:河南出版社,1991:229-276.
[3]梁節(jié)民.談施工項(xiàng)目管理與項(xiàng)目成本控制的關(guān)系[J].山西建筑,2005,31(1):144-145.

