改進的經驗模式分解方法及其在圖像邊緣檢測中的應用

郭艷光，程顯生

GUO Yan-guang, CHENG Xian-sheng

（內蒙古農業大學 職業技術學院 ，包頭 014109）

0 引言

圖像特征提取是圖像處理的關鍵技術之一，圖像邊緣檢測涉及圖像中研究對象的特征提取，在實際的數字圖像處理中，圖像的邊緣包含了圖像的位置、輪廓等特征，是圖像的基本特征之一，好的邊緣檢測算法對進行更高層次的圖像分析、理解等有不可忽視的實用價值和影響。

傳統的邊緣檢測算子中Roberts算子、Priwitt算子、Sobel算子、Canny算子等，將邊緣點理解為灰度突變點，通過不同的算子提取。但是，噪聲也是圖像灰度變化中的高頻成份，檢測結果噪聲較多；Gauss-Laplace和Canny算子較好的實現了圖像邊緣提取，但不能滿足實際中對圖像邊緣提取的要求；還有小波方法、基于熱傳遞方法、廣義模糊算子方法等同樣存在漏檢邊緣、模糊等缺陷。

二維經驗模式分解方法在非平穩信號的處理應用中具有很多獨特的優點。因此，把經驗模式分解方法應用到邊緣提取中，能提取出具有良好性質和結果的邊緣。但經驗模式分解最大的缺點是算法的時間復雜度大。本文將詳細闡述EMD的原理及其實現方法，介紹一種快速經驗模式分解方法并將其應用于圖像邊緣提取，將圖像中的邊緣快速有效的提取出來。

1 EMD原理

一維EMD的基本思想是：選取區域范圍，從圖像中找出信號中每個區域的局部極大值和局部極小值點，對極大值點和極小值點分別進行曲線插值，獲得信號的上、下包絡線，計算平均包絡線，計算原信號與平均包絡線的差值，然后利用篩選算法把符合模態函數（IMF）的信號分解出來。循環獲得頻率逐漸降低的多個模態函數。

模態函數必須滿足：1）數據序列x(t)的極值點數目與零點數目之差少于2個，2）上、下包絡的均值為零。第二個條件較為苛刻，將其用另外的標準代替：

式中hk(t)是IMF分量提取模塊中本次循環過程中求得的平均包絡，hk-1(t)是上次循環過程中求得的平均包絡，0……T是平均包絡線所包含的時刻。SD值一般在0.2-0.3。

二維EMD分解實現過程：

1）對所給圖像求取曲面局部極值點，包括所有局部極大值和極小值。

2）求取均值包絡曲面。極值點選取之后，對各極大值點和各極小值點分別進行曲面擬合，經插值后得到極大值點曲面包絡和極小值點曲面包絡，將兩曲面數據求平均得到均值包絡曲面。

3）計算原始曲面與均值包絡曲面。

4）與一維相似需計算終止條件。

重復步驟1～3，直到滿足給定的終止條件得到第一個模態函數IMF1,用原圖像減去第一個模態函數得到第一個殘余（residue），對殘余重復步驟1～步驟4，依次得到圖像的N個固有模態函數和第N個殘余。根據此方法對圖像進行分解，結果為下圖所示：

2 改進的BEMD

改進的BEMD原理：

目前，二維EMD已廣泛應用在圖像處理領域的諸多研究方向，也取得了一些可喜成果，但是二維EMD算法的時間復雜度一直是一個難以解決的問題，直接影響了它的應用范圍。本文針對二維EMD算法中運行時間最長的求取上下包絡進行改進，具體算法如下：

1）初始化r0(x,y)=f(x,y)，N=1；f(x,y)是原圖像，x,y是圖像的大小，i是分解的IMF數目；

2）對所給圖像求取曲面局部極值點，包括所有局部極大值max(x,y)和極小值min(x,y)；

3）求第N個模態函數

（1）初始化： i=1，j=1，i，j為圖像的大小，win=3,5,…,3+2N（N為分解的特征函數的個數）；

（2）以點（i,j）為中心，覆蓋到與它間距為(win-1)/2)的行和列中所有的點，構成win行win列矩陣（如果超出邊界，則取邊界值），計算矩陣中最大值和最小值的數目；

（3）如果局部最大值和最小值的數目相等，則計算該win行win列矩陣平均值avg。如果最大值和最小值的數目不相等，則win=win+2，跳轉到2步，當win=3+2N時最大值和最小值的數目還不相等，則計算win行win列矩陣平均值avg(i,j)；

（4）循環得到圖像中每一點的平均值avg(i,j)；

（5）IMF=r(i,j)-avg(i,j)，求出第一個模式函數IMF；

4）循環得到i個IMF。改進的BEMD部分程序：

根據上述算法將圖像進行二維EMD分解，得到N個IMF，結果如下圖所示：

Image(128*128)

mode1

mode2

mode3

mode4

Image(512*512)

mode1

mode2

mode3

mode4

改進的BEMD算法避免了用插值方法求包絡面，減少了時間復雜度，有效的增強了算法的可用性。

3 用改進的BEMD算法提取圖像邊緣

通過對圖像進行分解得到多個模態函數，第一個模式中包含大多邊緣信息，采用圖像二值化方法或結合其他邊緣檢測算法提取邊緣。本文采用改進的BEMD分解圖像、二值化方法提取邊緣（閾值為0）。

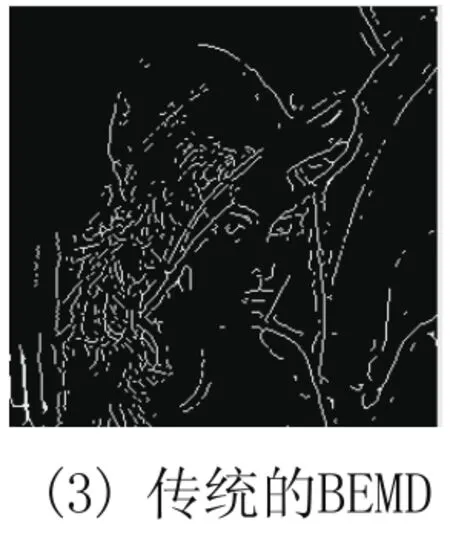
與傳統邊緣檢測算法的比較結果如下圖所示：圖(1)采用Sobel算法，圖(2)采用Canny算法，圖(3)采用傳統的BEMD算法，圖(4)、(5)采用改進的BEMD算法。實驗結果表明，采用改進的BEMD算法能更加清楚的提取邊緣、算法效率較高。

4 結論

本文給出了經驗模態分解(EMD)的實現方法，針對實現BEMD求取包絡面時間復雜度大現象，提出了一種改進的BEMD算法，該方法避免了求解大型線性方程組以及大矩陣，降低了時間和空間復雜度，提高效率。實驗結果證明了該方法的可行性和優越性。

[1] Huang N E,Shen Z,Long S R,et al.The empirical mode decom position and the Hilbert spectrum for nonlinear and nonstationary times series analysis[J].Proc R Soc Lond A,1998,454：903-995.

[2] NORDEN E.HUANG,SHEN Z,Long S R.The Empirical Mode Decomposition Method and the Hilbert Spectrum for Non-Stationary Time Series Analysis[J].Proc.Royal.Soc.London A,1998,454(A)：903-995.

[3] 米蘭,許海波.基于邊緣提取的圖像拼接[J].計算機應用研究,2007,25(5)：318-320.

[4] 沈濱,崔峰,彭思龍.二維EMD的紋理分析及圖像瞬時頻率估計[J].計算機輔助設計與圖形學學報,2005,17(10)：2345-2352.

[5] 張小薊,張歆,孫進才.基于經驗模態分解的目標特征提取與選擇[J].西北工業大學學報,2006,24(4)：453-456.

[6] 萬 建,任龍濤,趙春暉.二維EMD應用在圖像邊緣特征提取中的仿真研究[J].系統仿真學報,2009,21(3)：799-801.

[7] 宋立新,高鳳嬌,郗朝暉.二維EMD分解方法的比較與改進[J].電子與信息學報,2008,30(12)：2890-2893.

[8] 劉忠軒,彭思龍.方向EMD分解與其在紋理分割中的應用[J].中國科學(E輯)—信息科學,2005,35(2)：113-123.