山體地形下低矮房屋數值風洞模擬的計算域設定

崔利民,彭興黔,時凌琳,張春暉,喬常貴

(華僑大學土木工程學院,福建泉州362021)

山體地形下低矮房屋數值風洞模擬的計算域設定

崔利民,彭興黔,時凌琳,張春暉,喬常貴

(華僑大學土木工程學院,福建泉州362021)

針對山體地形下低矮房屋數值風洞模擬,研究其計算域大小的設定問題,并提出設置的參考方法.通過建立正弦山丘輪廓函數,對4種不同形狀因子的山丘進行計算流體動力學數值模擬.采用CFX軟件作為計算平臺,對影響計算結果精度的各個參數進行分析,在此基礎上,提出合理的取值范圍.

山體地形;低矮房屋;計算流體動力學;數值模擬;計算域

在我國沿海臺風多發地區,低矮房屋的抗臺風是一個現實而又亟待解決的問題[1].建造在復雜山體地形上的低矮建筑具有不同的地形地貌特征,因而風場條件各不相同.在臺風來時,受到特殊地形對風場的負面作用,加大了結構損壞的可能性,易造成嚴重的人員傷亡及經濟損失.目前,國內外在山體地形對低矮房屋建筑表面風荷載影響的研究還很少[2].利用計算流體動力學(CFD)數值模擬技術對建筑物繞流進行模擬時,要獲得理想的計算精度,其中一個重要的方面是計算域的設定.對建筑物表面風壓進行數值模擬時,在距離建筑較遠的地方要人為設置幾個壁面,使求解域封閉.設置求解域的大小與計算精度密切相關,太小會對建筑物表面風壓分布產生影響,太大又會增加計算網格數量,影響計算速度[3].由于山體地形下低矮房屋數值風洞模擬,與國內外所做的其他數值風洞模擬有所區別,因此不能簡單地根據已有經驗設定計算域.本文針對山體地形下低矮房屋數值風洞模擬,研究計算域大小設定的問題.

1 計算模型

針對三維正弦山丘單體,低矮房屋模型選取典型的二層雙坡屋面房屋,模型長度方向12 m,寬度方向8 m,檐口高7 m,屋面坡度30°,如圖1所示.由于三維正弦山丘在豎直方向上各向對稱,且房屋的幾何尺寸遠小于山丘,來流方向對計算域大小取值影響不大.因此,主要針對房屋位于山丘正前方的工況進行研究,計算模型如圖2所示.圖2中,房屋與山腳的間距s取24 m.山丘中軸線剖面輪廓函數選取正弦函數[4],即

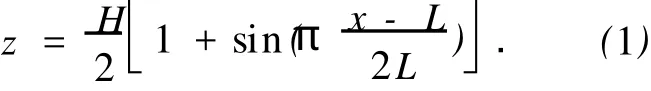
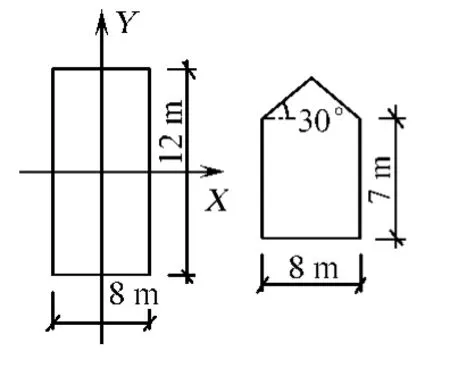
圖1 低矮房屋尺寸Fig.1 Size of low-rise houses

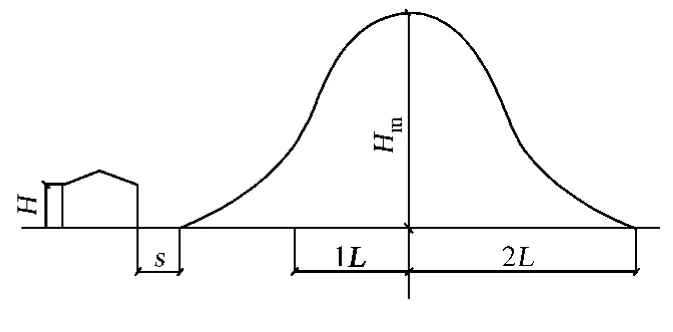
圖2 計算模型Fig.2 Computationalmodel

當L值一定時,山丘的輪廓形狀則取決于山高Hm.定義山丘形狀因子為

選取L=50 m,形狀因子(R)分別取0.5,1.0,1.5,2.0進行分析,坐標原點(0,0,0)設置在低矮房屋中軸線上的山丘山腳處.

2 計算域高度的設置

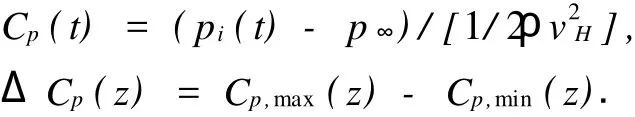
計算域高度的設定主要與山丘的形狀和尺寸有關.測點的平均風壓系數Cp(t)及z高度處水平剖面上平均風壓系數極差ΔCp(z)[5]為式中:pi(t)為測點的風壓值;p∞為參考點靜壓;ρ為空氣密度;vH為參考點的風速;Cp,max(z),Cp,min(z)分別為z高度處水平面上平均風壓系數的最大值和最小值.ΔCp(z)的大小可以衡量計算域頂面對模型表面平均風壓分布的影響,將其作為選取計算域高度的指標.ΔCp(z)值越大,說明該高度平面對模型周圍風場的影響越大;ΔCp(z)值越小,則對風場的影響越小,表明該高度已不在建筑物周圍的風場區[6].

當形狀因子R為0.5時,不同風向角下的ΔCp(z)隨距離地面高度的變化曲線,如圖3(a)所示.從圖3(a)可得知,當距離地面高度大于4L時,曲線逐步趨于平緩;當距離地面高度為6L時,ΔCp(z)小于0.02,則該高度已不影響模型周圍的風場.因此,建議R為0.5時的計算域高度取值范圍為4L～6L.各風角下的變化曲線基本重合,說明在設置計算域的高度時,風向角的影響并不明顯.因此,以下其他形狀因子主要以0°風向角為例進行說明.

當風向角為0°時,不同形狀因子下的ΔCp(z)隨高度變化曲線,如圖3(b)所示.由圖3(b)可知,計算域高度大于4L時,曲線逐步趨于平緩;當距離地面高度為5L時,ΔCp(z)僅為0.02,認為該高度已不影響模型周圍的風場.因此,建議R為1.0的計算域高度取值范圍為6L～8L.

由圖3(b)還可以看出,當距離地面高度大于8L時,曲線逐步趨于平緩;當距離地面高度為10L時, ΔCp(z)小于0.02,認為該高度已不影響模型周圍的風場.因此,建議R為1.5,2.0時的計算域高度取值范圍為8L～10L.

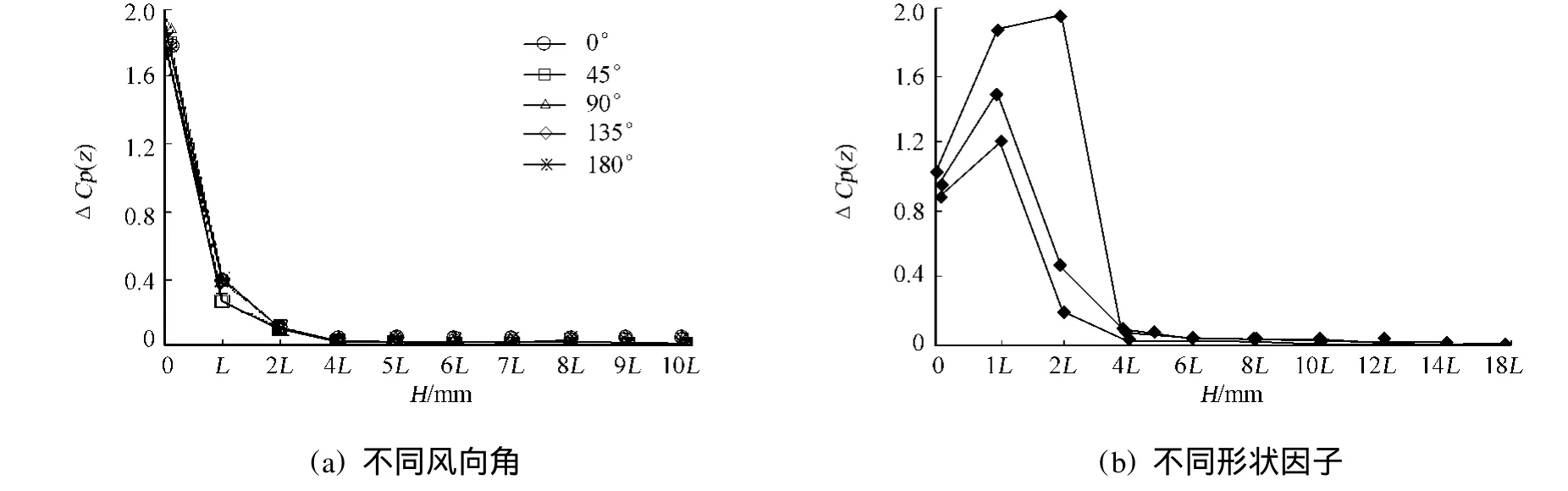
圖3 ΔCp(z)隨高度變化曲線Fig.3 Curve betweenΔCp(z)and height

3 計算域長度的設置

在已經確定好的計算域高度范圍內,選取幾個具有代表性的水平剖面,通過分析這些平面內的相對靜壓分布,確定計算域的大小范圍.當R為0.5時,不同風向角下不同高度平面內的相對靜壓分布圖,如圖4所示.由圖4可知,就大范圍而言,風壓分布情況主要是由山丘決定的,低矮房屋由于體積比較小,對計算域的整體風壓分布影響較小.由于山丘的形狀是沿著高度方向雙向對稱的,因此可以忽略風向角的影響,主要取0°風向角為研究對象.

山丘中心正上游對計算域上游長度的影響最大,且各風向角下的相對靜壓分布曲線基本沿Y軸對稱.所以,沿著此方向取不同高度處測點的相對靜壓,通過相對靜壓為零來確定計算域上游長度L1的取值范圍.相對靜壓隨計算域上游到模型迎風面的距離變化曲線,如圖5所示.

由圖5可知,當R為0.5時,在0L～6L范圍內,相對靜壓變化較大,6L時各個測點的相對靜壓基本為零.因此,L1取4L～6L;同理,當R分別為1.0,1.5,2.0時,L1可取6L～8L.

圖4 順風向水平剖面相對靜壓等壓線分布圖Fig.4 Relative static p ressure contours fo r along-w ind ho rizontal p rofile

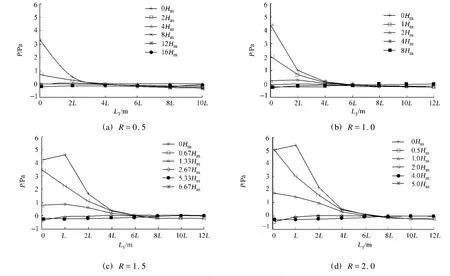
圖5 相對靜壓隨L1的變化曲線Fig.5 Curve of relative static p ressure to L1

氣流遇到山丘時,在山丘迎風面的一部分氣流上升越過山丘,一部分氣流下沉降至地面,另一部分則繞過山丘的兩側向背后流去,在山丘的背后產生尾流.計算域下游長度L2不能設置太小,否則會導致出口處出現回流,影響計算結果的精度.

在已經確定好的計算域高度范圍內,選取幾個具有代表性的水平剖面,通過分析這些平面內的相對靜壓分布,可以估計L2的范圍.相對靜壓隨計算域下游到模型迎風面的距離變化曲線,如圖6所示.

從圖6可以看出,當R為0.5時,相對靜壓為零的等壓線沿水平方向延伸較長.在0L～8L范圍內,相對靜壓變化較大,10L時各個測點的相對靜壓基本接近于零.因此,L2可取8L～10L.同理,當R分別為1.0,1.5,2.0時,L2的取值范圍分別為8L～10L,10L～12L,12L～14L.

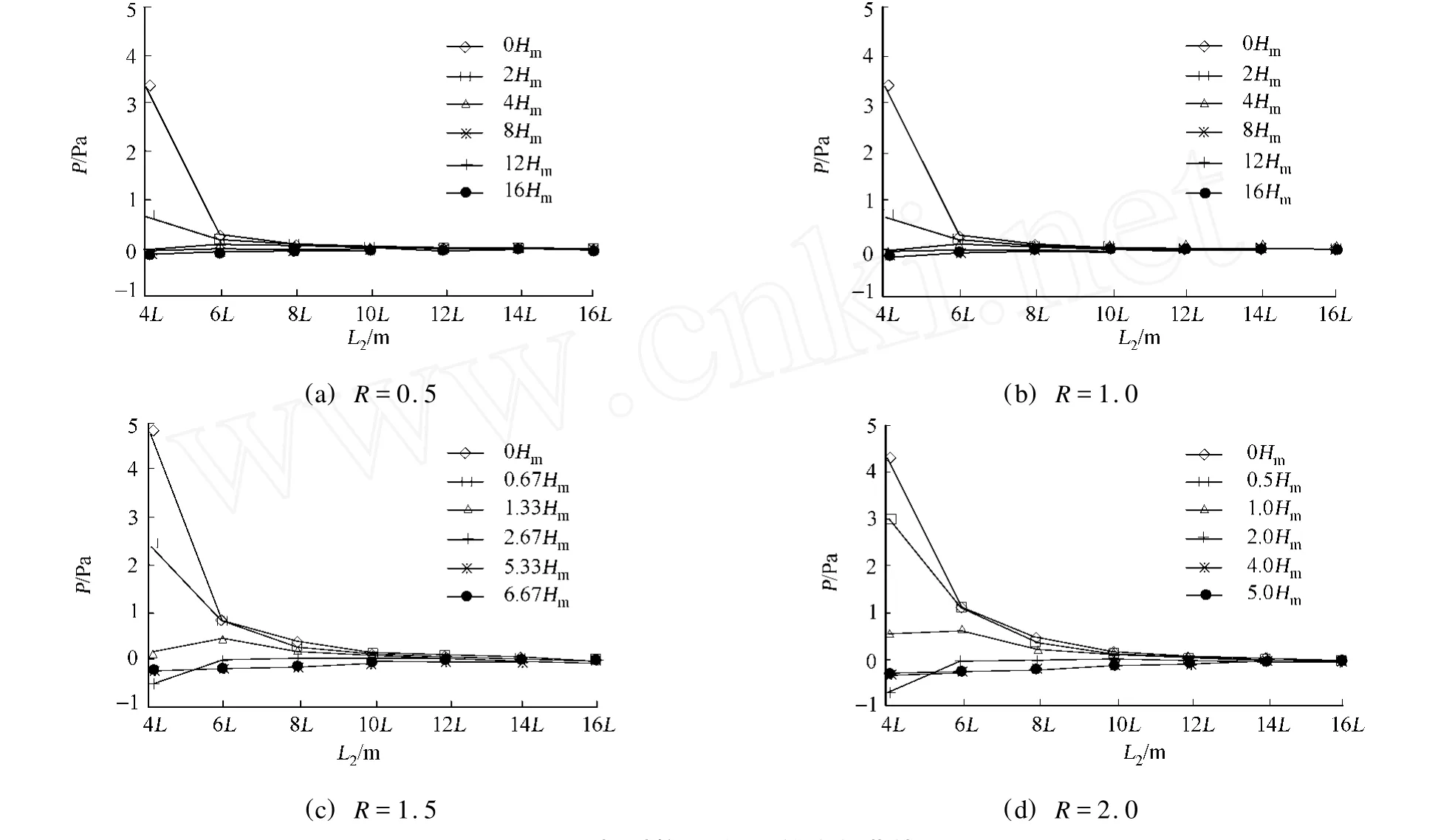
圖6 相對靜壓隨L2的變化曲線Fig.6 Curve of relative static p ressure to L2

4 計算域寬度的設置

由于來流有一部分氣流從山丘側面繞過,在側面產生的繞流,使風速變大、流場變化復雜.通過相對靜壓分布的判斷可以取定計算域寬度(B)的范圍[7].由圖4可知,山丘中心在橫風向方向受計算域側面的影響最大.

因此,在山丘中心沿橫風向方向不同高度處,測點的相對靜壓值隨B1的變化曲線,如圖7所示.圖7中,B1=(B/2)-2L.從圖7可知,當R為0.5,B1為10L時,相對靜壓接近為0 Pa,曲線趨于平緩一致,計算域寬度B為20L.因此,B的取值范圍為20L～24L.同理,當R分別為1.0,1.5,2.0時,B的取值范圍分別為24L～28L,28L～32L,28L～32L.

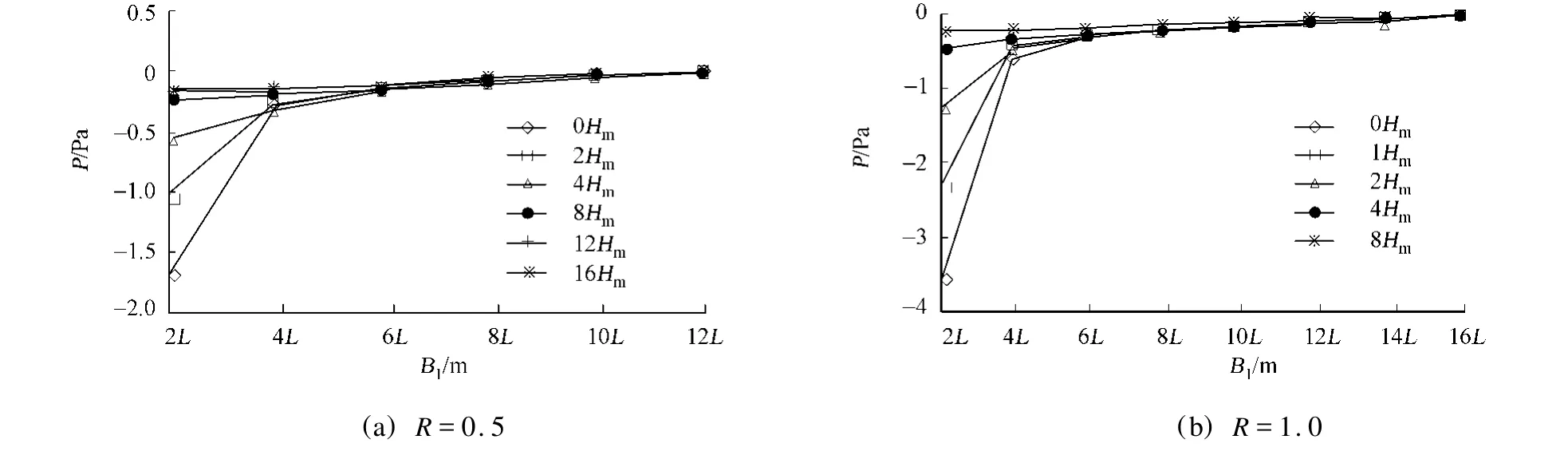
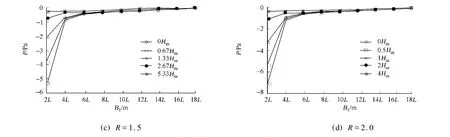
圖7 相對靜壓隨B1的變化曲線Fig.7 Curve of relative static p ressure to B1

5 結束語

研究山體地形下低矮房屋數值風洞模擬中的計算域設置問題,得到計算域高度、寬度,以及長度的建議取值范圍.需要注意的是,數值風洞的計算域設置應滿足阻塞度小于5%的相關要求.

[1] 周顯鵬,彭興黔,張松.帶懸挑女兒墻雙坡屋面風壓的數值模擬分析[J].華僑大學學報:自然科學版,2008,29(2): 289-293.

[2] 陳平.地形對山地丘陵風場影響的數值研究[D].杭州:浙江大學,2007.

[3] 侯愛波,汪夢甫.建筑數值風洞的基礎研究[J].湖南大學學報:自然科學版,2007,34(2):21-24.

[4] TAMURA T,OKUNO A,SUGIO Y.LESanalysisof turbulent boundary layerover 3D steep hill covered with vegetation[J].JWind Eng Indus Aerodyn,2007,95(9/11):1463-1475.

[5] 喬常貴,彭興黔,時凌琳,等.港口集裝箱群數值模擬中計算域設置的研究[J].鄭州輕工業學報:自然科學版,2008, 23(2):104-107.

[6] 孫曉穎,許偉,武岳.鈍體繞流中的計算域設置研究[C]∥第十三屆全國結構風工程學術會議.大連:[s.n.],2007: 1036-1041.

[7] 孫珩,黃素逸.建筑物周圍流場數值模擬的研究進展[J].環境科學進展,1999,7(6):76-83.

Computational Domain Setting about Numerical W ind Tunnel in the Simulation of the Low-Rise Housing in the M oun tain Terrain

CU ILi-ming,PENG Xing-qian,SH ILing-lin, ZHANG Chun-hui,Q IAO Chang-gui
(College of Civil Engineering,Huaqiao University,Quanzhou 362021,China)

Based on the numerical w ind tunnel simulation of low-rise housing in themountain terrain,the computational domain setting of the w ind tunnel is investigated,and one method is put fo rward.Establishing sinusoidal hill contour function,four hills of different shape factors is simulated numerically by the computational fluid dynamics.Using CFX softw are,the parameters that affect the accuracy of the results isanalyzed,then the reasonable domain of the w ind tunnel is given.

mountain terrain;low-rise house;computational fluid dynamics;numerical simulation;computational domain

TU 312+.1;P 435+.1

A

(責任編輯:錢筠 英文審校:方德平)

1000-5013(2010)04-00463-05

2009-07-29

彭興黔(1959-),男,教授,主要從事結構抗風的研究.E-mail:pxq@hqu.edu.cn.

福建省自然科學基金資助項目(2009J01255);福建省廈門市科技計劃高校創新項目(3502Z20083039);福建省泉州市科技計劃重點項目(2007G7);湖南省風工程與橋梁工程重點實驗室開放基金資助項目(2009-01)