CeO2的電子結構，光學和晶格動力學性質:第一性原理研究*

李沛娟 周薇薇 唐元昊 張華 施思齊

(浙江理工大學物理系，光電材料與器件中心，杭州310018)

(2009年7月9日收到;2009年9月14日收到修改稿)

CeO2的電子結構，光學和晶格動力學性質:第一性原理研究*

李沛娟 周薇薇 唐元昊 張華 施思齊?

(浙江理工大學物理系，光電材料與器件中心，杭州310018)

(2009年7月9日收到;2009年9月14日收到修改稿)

.基于考慮了Ce-4f電子間的庫侖作用U和交換作用J的LDA+U方案，應用第一性原理計算系統研究了CeO2的電子結構，光學和晶格動力學性質.電荷密度和電子局域函數的分布特征表明，CeO2是屬于共價鍵的絕緣體.介電常數、玻恩有效電荷張量和聲子色散曲線的計算值和相應的實驗結果符合得比較好.

電子結構，光學性質，晶格動力學，第一性原理計算

PACC:7115A，7630K，7125，6320D

1. 引言

二氧化鈰(CeO2)是一種技術上重要的氧化物材料.例如，它被廣泛應用于處理機動車尾氣NOx，CO和碳氫化合物的三效催化劑中［1—3］.另外，在未來的制氫和凈化技術中，特別是對于水煤氣的轉化反應和酒精與水的混合物轉化成氫的反應有著很好的應用前景［4，5］.這些技術上的應用主要源自于CeO2中氧空位形成和擴散的便利性.同時，CeO2的高介電常數和CeO2-Si之間的小晶格失配(～0.35%)使得其適合制作絕緣層-硅結構等微電子器件［6］.

理解這種稀土金屬氧化物的基本物理性質對促進其更廣泛的應用是必要的.實驗上，已經有一些關于CeO2成鍵本質和Ce-4f軌道占據情況的研究［7—10］.然而，同樣是基于Anderson雜質模型［11］的Ce-4f軌道占據分析，卻出現了兩種不同的觀點: Fujimori［8］和Normand等人［9］提出CeO2中的Ce-4f電子應該是處于一個有0.5占據的混合價態; Wuilloud等人［10］的一個類似實驗結果則顯示CeO2中的Ce-4f軌道幾乎是未被占據的，Ce離子為+4價態.因此，依賴于關于Ce-4f軌道占據的不同觀點，也出現了關于CeO2成鍵本質的不同描述:離子鍵和共價鍵.CeO2的晶格動力學性質是另一個重要的課題，但實驗或理論上的報道卻比較少.紅外反射測量給出了CeO2在Γ點的聲子頻率［7，12，13］. Clausen等人［14］的非彈性中子散射實驗報道了500cm－1以下沿著［ξ00］和［ξξ0］方向的聲子頻率.就我們所知，到目前為止只有Yamamoto等人［15］和Sevik等人［16］進行了CeO2晶格動力學性質的第一性原理計算，采用的方案是局域密度近似和超軟贗勢平面波法.

盡管存在上面所提及的有關CeO2成鍵本質的爭論及其在應用上的重要性，但是卻少見關于該化合物的第一性原理研究.一個可能的原因是在傳統的密度泛函理論中很難給出一個合理的關于Ce-4f電子的描述.然而，對于一個含有多價態金屬的系統［17，18］，特別是鑭族，一個準確的基態性質描述要求考慮到f電子的強關聯影響.在本文中，基于考慮了Ce-4f電子間的庫侖作用U和交換作用J的LDA +U方案，應用第一性原理計算系統研究了CeO2的電子結構，光學和和晶格動力學性質，并與已有的實驗和理論數據進行了系統的比較.

2. 計算細節

計算應用的是基于密度泛函理論的第一性原理方法，離子核和電子之間的相互作用采用凝聚芯投影綴加波法(PAW)［19］.使用的計算軟件包是VASP［20］.Ce的5s，5p，5d，4f，6s電子以及O的2s和2p電子被視為價電子.采用局域密度近似(LDA)［21］描述電子交換-關聯能.為描述Ce-4f電子之間的庫侖作用，用Dudarev等人［22］提出的旋轉不變方法(Rotationally Invariant Approach)在LDA中增加了Hubbard參數U(LDA+U)，這里只有庫侖U和交換J之差(Ueff=U－J)有意義.我們采用Silva等人［23］建議的Ueff值(5.3 eV)，它是由Fabris等人［24］用Cococcioni和de Gironcoli［25］提出的線性回歸方法通過自洽計算而得到的.由于CeO2是無磁矩稀土金屬氧化物［26］，所以沒有考慮自旋極化.電子波函數用平面波展開，平面波動能的截止能為500 eV，采用4×4×4 Monkhorst-Pack類型［27］的k點進行布里淵區的積分，其高斯展寬為0.20 eV［28］，這些參數使得總能量收斂到0.01 meV/atom.為了精確計算電子態密度(DOS)，采用了8×8×8 k點，且使用了Blchl［29］的修正四面體方法.

為了計算聲子色散關系，我們采用Parlinski等人［30］提出的直接從頭力場常數方法.由指定的原子位移導致周圍原子上的受力可以通過Hellmann-Feynman定理算出.整合這些受力可以構建力場常數矩陣和動力學矩陣，采用基于簡諧近似的直接方法能夠求解動力學矩陣.為了避免因周期性邊界條件而產生的兩個位移原子之間的相互作用，采用相對大超晶胞進行力場矩陣的計算是必要的，這里，我們嘗試使用2×2×2單胞(96個原子).

一般來講，在Γ點的紅外光學模通常會由于長程的庫侖作用分裂成縱向(LO)光學模和橫向(TO)光學模(LO/TO分裂).Kunc和Martin［31］指出，在Γ點的LO/TO分裂不能由直接的方法得到，只有TO光學模的計算不需要進一步近似.一種解決方法是用一個拉長的超晶胞導出LO/TO分裂.然而，對目前的系統采用拉長的超晶胞超出了計算資源的限制.另一種辦法是，采用如下的非解析動力學矩陣來獲得LO/TO分裂:

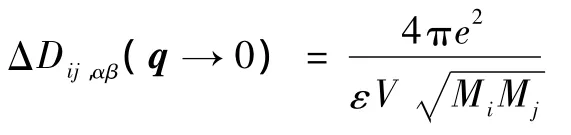
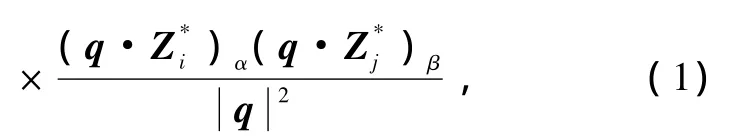
這里q是波矢，ε是光學介電函數，V是原胞的體積，Mi和Z*i分別是第i個原子的質量和玻恩有效電荷張量，α和β是笛卡爾坐標方向指數.

3. 結果與討論

3.1. 電子結構

CeO2晶體為螢石結構(面心立方)，其空間群為Fmm.計算給出的平衡晶格參數為5.400，這與5.411的實驗值［32］符合得非常好.圖1顯示了體相CeO2的局域分波態密度(LPDOS).最高占據的價帶主要是O-2p，并伴隨著Ce-4f和Ce-5d的一些貢獻，費米能級之上窄的空帶主要歸因于Ce-4f態.O-2p帶的寬度為4.15 eV，這與實驗值［10］和以前的理論計算值［33，34］符合得非常好.O-2p價帶頂和未占據的Ce-4f，Ce-5d帶之間的帶隙分別為2.377 eV和5.186 eV，這與3.0 eV和6.0 eV的實驗值［10］是可比的.需要說明的是，帶隙的低估是LDA計算的一個典型不足之處，LDA+U正是為了彌補LDA帶隙的不足而引進的修正，而且對帶隙的修正是依賴于Hubbard參數U的.正如圖1所顯示的，電子態密度的計算結果能清楚地表明，CeO2是一個具有寬帶隙的絕緣體，這與實驗［10］是一致的.

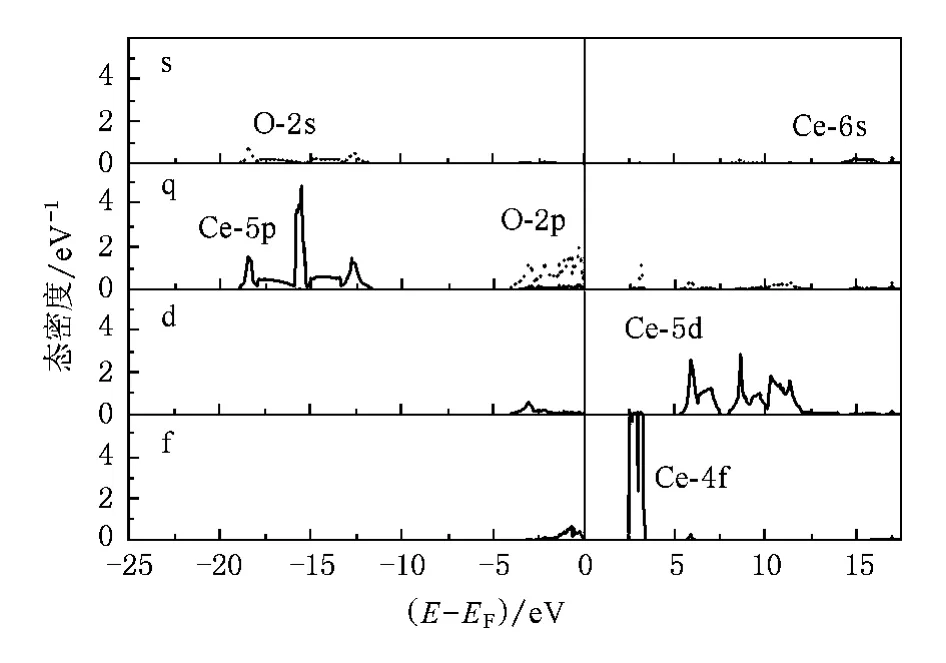
圖1 體相CeO2中Ce(實線)和O(虛線)的分波電子態密度

現在我們討論CeO2的成鍵本質.從圖1可以看出，在O-2p態中存在著一些Ce-5d和Ce-4f的特征.Koelling等人［34］的計算也同樣得到了這個結果，這說明Ce-4f被部分占據是合理的.因此，在O-2p帶中存在著一個非零的Ce-4f和Ce-5d態密度的事實提供了Ce-O鍵為共價鍵的一些證據.為了進一步地理解CeO2中Ce-O鍵的成鍵本質，我們繪出了CeO2(110)面的價電子密度分布圖，如圖2(a)所示.可以看出，Ce和O原子之間存在顯著的電荷重疊，換句話說，Ce-4f(5d)與O-2p之間的確存在著軌道雜化.另一方面，電子的局域函數(ELF)［35］是一個重要的基態性質，用它可以對不同種類之間的成鍵進行區別.在DFT計算中，ELE被定義為［1+ (D/Dh)2］－1，這里的D是由于泡利不相容原理所產生的額外局部動能.因而D可以從τ-tW中獲得，是Kohn-Sham局部動能(τ=1/2Σ|Δφi|2，φi是Kohn-Sham軌道)，ΔtW是τ在沒有包含泡利不相容原理時的值(～|ρ|2/ρ，ρ是電荷密度).Dh描述了均一電子氣的D(～ρ5/3).根據這種定義，ELF可以取的值為0到1，這里的1對應于完全的局域性.圖2(b)顯示了CeO2(110)面ELF，Ce和O原子之間的ELF值是0.5，這有力地證明了CeO2中Ce-O之間共價鍵的存在，即說明了CeO2是呈現共價鍵的絕緣體.無論如何，我們的理論計算與通過光學反射技術獲得的實驗結果［7］符合較好.

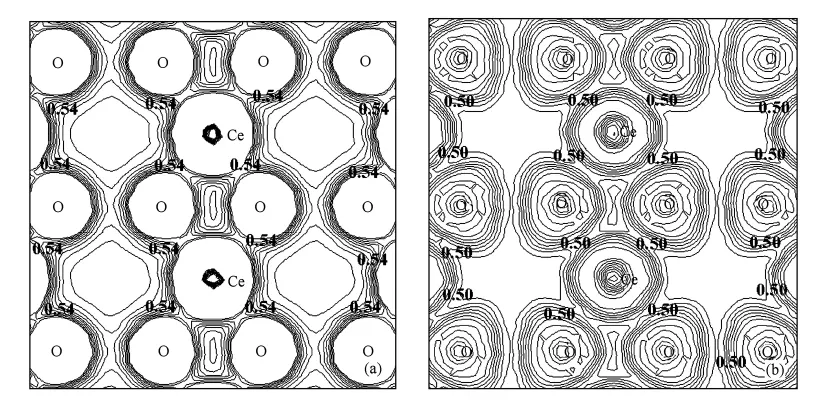
圖2 CeO2(110)面的(a)價電子密度分布(等高線以0.06 e/3的間隔從0.0 e/3到0.6 e/3)和(b)電子局域函數(等高線以0.1的間隔從0.0到1.0)

3.2. 玻恩有效電荷張量和光學性質

在計算細節部分，我們討論了在Γ點的紅外光學模通常會由于長程的庫侖作用發生所謂的LO/ TO分裂.這個庫侖作用與玻恩有效電荷張量有著直接的關聯，例如，第i個原子的位移(Δu)導致一個有限的偶極矩p，

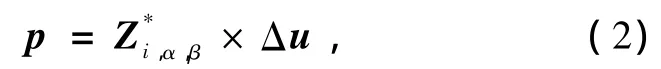
這里的Z*i，α，β是玻恩有效電荷張量，Δu是第i個原子在單胞中的位移.根據極化理論［36，37］，結構發生扭曲引起的極化為

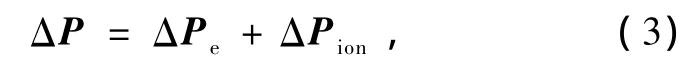
這里的ΔPe是由Berry相位極化方法得到的電子部分的貢獻，而ΔPion是離子部分的貢獻，

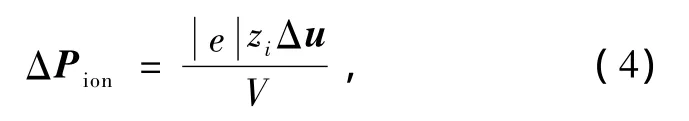
這里的zi是第i個原子的原子序數，V是單胞的體積，Δu是第i個原子在單胞內的位移.只要ΔP知道，那么對于β組份的玻恩有效電荷也就可以通過下面公式得到:

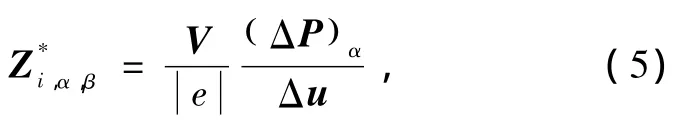
式中α表示極化方向.在CeO2中，Ce和O分別占據著4a和8c的Wyckoff位置.由于Fm-3m高度的對稱性，它們的玻恩有效電荷張量都是各向同性且對角化的，即Z*ij=Z*δij.計算所得的玻恩有效電荷張量分別是Z*Ce=5.4794和Z*O=－2.7397，ΣZ*=0表明了有效電荷張量的計算結果是合理的.

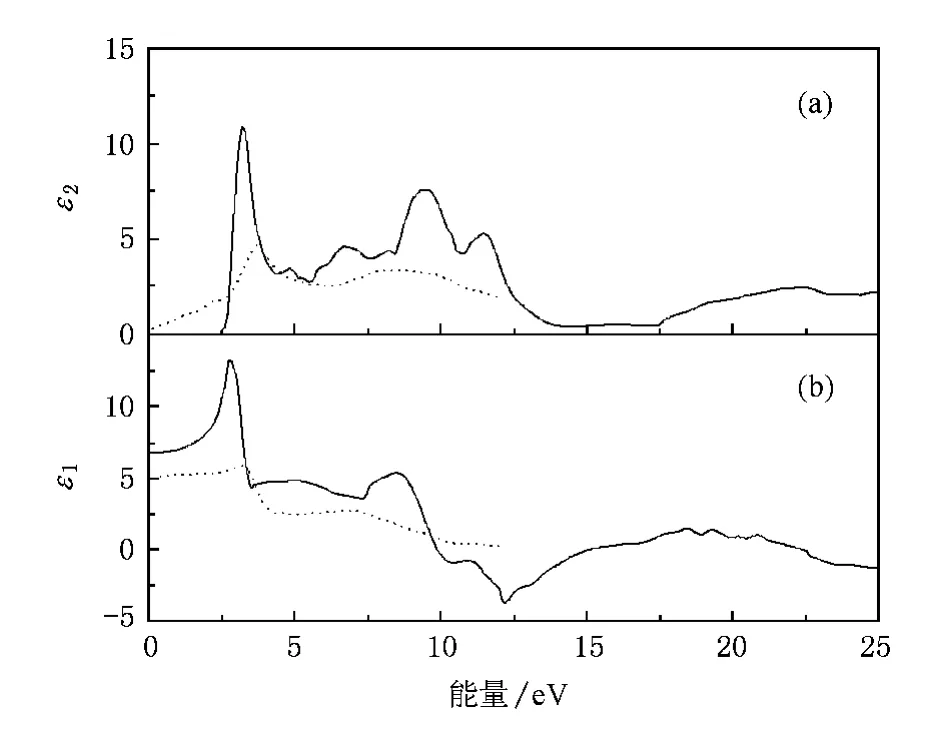
圖3 CeO2介電函數的(a)虛部ε2(E)和(b)實部ε1(E)與光子能量的關系圖(虛線為文獻7的實驗數據)

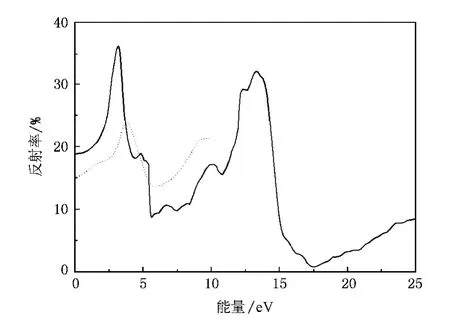
圖4 CeO2的反射率與光子能量的關系圖(虛線為文獻7的實驗數據)

圖3和圖4分別呈現了CeO2的介電函數和反射率與光子能量的關系圖，作為比較，虛線為來自于Marabelli和Wachter［7］對CeO2單晶反射率的測量數據.從實驗曲線可以看出，在3.66 eV和8.46 eV處分別出現一個尖峰和平緩的峰.圖3(a)所示ε2(E)的計算曲線在3.2 eV處出現了陡然的增加，第二個和第三個主峰分別位于9.5 eV和22.3 eV，因此，可以說計算曲線和實驗結果符合較好.另一方面，實驗和計算所獲得的強度(峰高)之間存在著一些差異，這種差異可能是源于兩者所用的展寬不一樣.一般說來，更大的展寬導致導致更低的強度(峰高).由于在實驗結果中，所用的展寬沒有被給出，因此難以和我們的計算進行比較.

在圖3(a)中，ε2(E)的峰值源于從價帶到導帶的躍遷.根據偶極躍遷選擇定則，僅僅角動量量子數l的改變Δl等于1的躍遷才是允許的.位于3.2 eV的第一個峰被解釋為電子從Ce-5d態躍遷到Ce-4f態，而第二個峰則對應于Ce-5p→Ce-5d的躍遷，這與圖1所示的電子態密度曲線是一致的.事實上，正如文獻7所討論的，第一個峰的寬度主要由CeO2最高占據價帶的寬度來決定(大約4 eV，見圖1).此外，ε2(E)中第一個峰的復雜結構與－4 eV至費米能級間隔內電子態密度曲線的精細結構是相似的.

采用Kramers-Kronig變換公式，我們給出了介電函數的實部ε1(E)，如圖3(b)所示，計算曲線和實驗結果所顯示的主要特征相同.在2.8 eV和8.5 eV處的兩個峰分別對應于實驗曲線中的3.12 eV和7.32 eV.我們計算所得的靜態介電常數的值為6.7 eV，作為比較，實驗值為4.7(文獻［7］)，5.31(文獻［12］)，6(文獻［13］和［38］)，2.85(文獻［14］)和3.0(文獻［39］)，如表1所示.然而，Yamamoto等人利用LDA方法計算得到了一個更大的值為7.5［15］.這種類型的高估在HgI2等材料中也出現過［40］.類似于ε2(E)曲線的情形，對于ε1(E)中峰的強度，我們的計算值與實驗也存在差別.

圖4呈現了CeO2的反射率與光子能量的關系圖，來自文獻［7］的實驗數據用虛線表示.可以看出，反射率開始時約為18.89%，在3.2 eV處出現最大值36.84%，實驗上測量的反射率在3.66 eV處出現24%的最大值.因此，我們的計算結果與實驗上帶間躍遷的峰值符合較好.

3.3. 聲子色散關系和聲子態密度

我們計算了第一布里淵區中沿Γ-X-U(K)-Γ-LX-W-L高對稱方向的聲子色散關系，如圖5所示.因為原胞中有三個原子，所以存在三個聲學支和6個光學支.根據其對稱性分析(晶體點群:Oh)，在Γ點的光學支可分解為

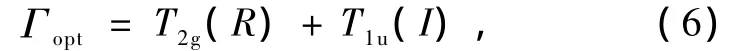
這里的符號R和I分別表示拉曼活性模和紅外活性模.T2g(R)和T1u(I)都是三重簡并的，另一個三重簡并的T1u模是聲學模.需要注意的是，紅外光學T1u模的簡并度由于存在LO/TO分裂而部分消失.

表1總結了Γ點的拉曼和紅外聲子頻率的計算值以及來自別處的計算和實驗結果.對于拉曼和T1u(LO)模，理論計算和實驗值吻合得很好.而對于T1u(TO)模，我們的計算值比文獻［12—14］所報道的值要高出約9%.而文獻［7］所報道的T1u(TO)值卻比我們的計算值和文獻［12—14］紅外測得的數據要更低.值得一提的是，對于T1u(TO)支在第一性原理計算中的高估在另外的諸如PbF［41］，BaF［41］22等螢石結構材料也被觀察到.

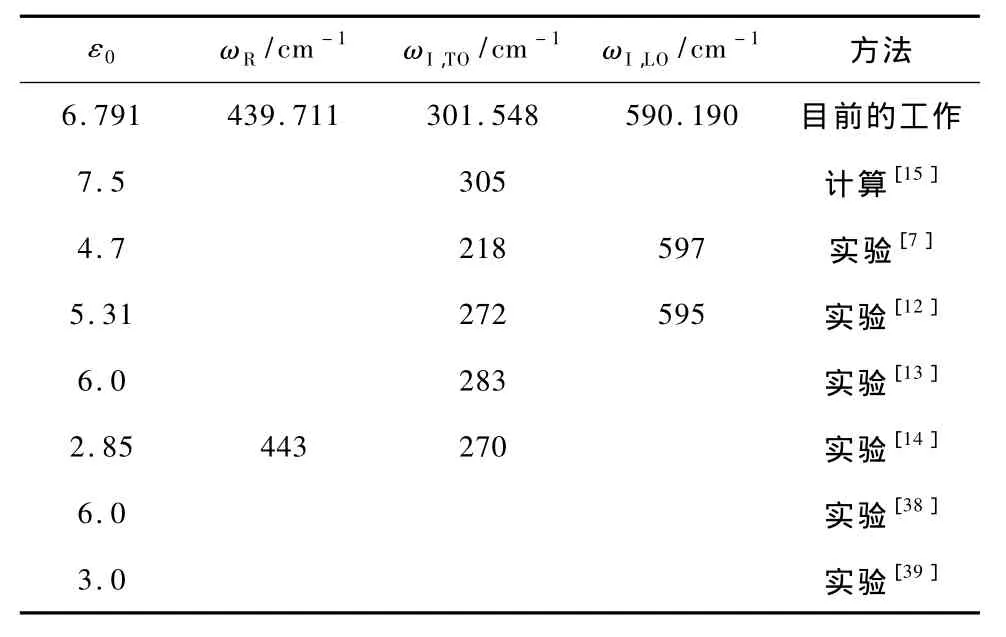
表1 靜態介電系數(ε0)，Γ點拉曼(ωR)和紅外聲子頻率(ωI，TO和ωI，LO)的計算值以及來自別處計算和實驗結果

圖5顯示了沿CeO2第一布里淵區一些高對稱方向的聲子色散曲線，為進一步和實驗比較的方便，Clausen等人［14］的中子散射實驗值在圖5中也被列出，但他們所報道的實驗數據只有沿Γ-X-U (K)-Γ-L方向且低于500cm－1的頻率.可以看出，我們計算的頻率與實驗結果總體上是相符合的.盡管T1u(TO)支在CeO2布里淵區中心的Γ點有9%的偏離，但當趨向布里淵區邊界X和L點時，T1u(TO)支的計算和實驗值卻符合得相當好.正如在別的螢石結構［41］中觀察到的那樣，聲子色散曲線的另一個特征是T1u(LO)支平緩的彌散性.

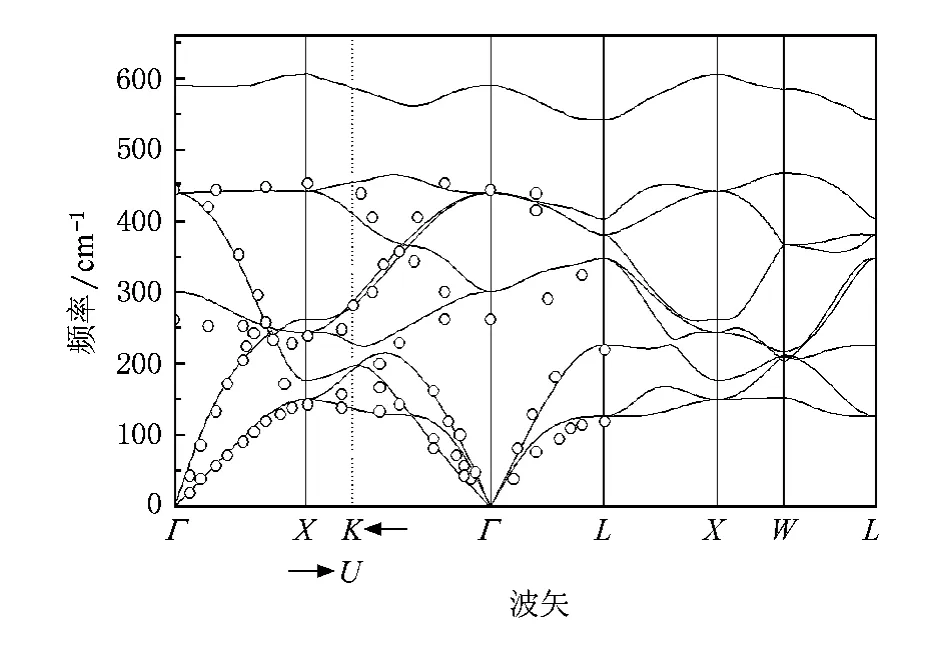
圖5 沿CeO2第一布里淵區一些高對稱方向的聲子色散曲線(離散的空心小圓圈為文獻14中的中子散射數據)

4. 結論

采用第一性原理密度泛函理論和LDA+U方法，系統研究了CeO2的電子結構、光學和晶格動力學性質.電荷密度和電子局域函數的分布特征表明，CeO2是呈現共價性質的絕緣體，這與通過光學反射技術獲得的實驗結果符合較好.介電常數、玻恩有效電荷張量和聲子色散曲線與實驗結果總體上是符合的.

［1］Park S，Vohs J M，Gorte R J 2000 Nature(London)404 265

［2］Dresselhaus M S，Thomas I L 2001 Nature(London)414 332

［3］Esch F，Fabris S，Zhou L，Montini T，Africh C，Fornasiero P，Comelli G，Rosei R 2005 Science 309 752

［4］Fu Q，Saltsburg H，Flytzani-Stephanopoulos M 2003Science 301 935

［5］Deluga G A，Salge J R，Schmidt L D，Verykios X E 2004 Science 303 993

［6］Inoue T，Yamamoto Y，Koyama S，Suzuki S，Ueda Y 1990 Appl. Phys.Lett.56 1332

［7］Marabelli M，Wachter P 1987 Phys.Rev.B 36 1238

［8］Fujimori A 1983 Phys.Rev.B 27 3992

［9］Normand F L，Fallah J E，Hiliaire L，Légaré P，Kotani A，Parlebas J C 1989 Solid State Commun.71 885

［10］Wuilloud E，Delley B，Schneider W D，Baer Y 1984 Phys.Rev. Lett.53 202

［11］Anderson P W 1961 Phys.Rev.24 41

［12］Mochizuki S 1982 Phys.Status Solidi B 114 189

［13］Santha N I，Sebastian M T，Mohanan P，Alford N M，Sarma K，Pullar R C，Kamba S，Pashkin A，Samukhina P，Petzelt J 2004 J. Am.Ceram.Soc.87 1233

［14］Clausen K，Hayes W，Macdonald J E，Osborn R，Schnabel P G，Hutchings M T，Magerl A 1987 J.Chem.Soc.，Faraday Trans. 283 1109

［15］Yamamoto T，Momida H，Hamada T，Uda T，Ohno T 2005 Thin Solid Films 486 136

［17］Lu Z S，Luo G X，Yang Z X 2007 Acta Phys.Sin.56 5382(in Chinese)［路戰勝、羅改霞、楊宗獻2007物理學報56 5382］

［18］Wei Y W，Yang Z X 2008 Acta Phys.Sin.57 7139(in Chinese)［魏彥嶶、楊宗獻2007物理學報57 7139］

［20］Kresse G，Furthmüller J 1996 Phys.Rev.B 54 11169

［21］Perdew J P，Zunger A 1981 Phys.Rev.B 23 5048

［22］Dudarev S L，Botton G A，Savrasov S Y，Humphreys C J，Sutton A P 1998 Phys.Rev.B 57 1505

［23］Silva J L F D，Ganduglia-Pirovano M V，Sauer J，Bayer V，Kresse G 2007 Phys.Rev.B 75 045121

［24］Fabris S，de Gironcoli S，Baroni S，Vicario G，Balducci G 2005 Phys.Rev.B 72 237102

［25］Cococcioni M，de Gironcoli S 2005 Phys.Rev.B 71 035105

［26］Wachter P 1982 Valence Instabilities edited by Wachter P and Boppart H(North-Holland，Amsterdam，1982)p145

［27］Monkhorst H J，Pack J D 1976 Phys.Rev.B 13 5188

［28］Methfessel M，Paxton A T 1989 Phys.Rev.B 40 3616

［30］Parlinski K，Li Z Q，Kawazoe Y 1997 Phys.Rev.Lett.78 4063

［31］Kunc K，Martin R 1982 Phys.Rev.Lett.48 406

［32］Gerward L，Olsen J S，Petit L，Vaitheeswaran G，Kanchana V，Svane A 2005 J.Alloys Compd.400 56

［33］Skorodumova N V，Ahuja R，Simak S I，Abrikosov I A，Johansson B，Lundqvist B I 2001 Phys.Rev.B 64 115108

［34］Koelling D D，Boring A M，Wood J H 1983 Solid State Commun. 47 227

［35］Silvi B，Savin A 1994 Nature(London)371 683

［36］King-Smith R D，Vanderbilt D 1993 Phys.Rev.B 47 1651

［37］Resta R 1994 Rev.Mod.Phys.66 899

［38］Guo S，Arwin H，Jacobsen S N，Jrrendahl K，Helmersson U 1995 J.Appl.Phys.77 5369

［39］Niwano M，Sato S，Koide T，Shidara，Fujimori A，Fukutani H，Shin S，Ishigame M 1988 J.Phys.Soc.Jpn.57 1489

［40］Ahuja R，Auluck S，Eriksson O，Wills J M，Johansson B 1996 Phys.Rev.B 54 10419

［41］Dubinin A，Winkler B，Knorr K，Milman V 2004Eur.J. Biochem.39 27

PACC:7115A，7630K，7125，6320D

*Project supported by the National Natural Science Foundation of China(Grant Nos.50730004 and 50802089)，Qianjiang Talent Project of Zhejiang Province(Grant No.2007R10028)，the Scientific Research Foundation for the Returned Overseas Chinese Scholars，State Education Ministry of China(Grant No.［2008］890)，and Natural Science Foundation of Zhejiang Province(Grant Nos.Y407188 and Y4090280).

?Corresponding author.E-mail:siqishihz@gmail.com

Electronic structure，optical and lattice dynamical properties of CeO2:A first-principles study*

Li Pei-Juan Zhou Wei-Wei Tang Yuan-Hao Zhang Hua Shi Si-Qi?
(Department of Physics，Center for Optoelectronics Materials and Devices，Zhejiang Sci-Tech University，Xiasha College Park，Hangzhou310018，China)
(Received 9 July 2009;revised manuscript received 14 September 2009)

The electronic structure，optical and lattice dynamical properties of CeO2are studied using first-principles density functional theory taking into account the on-site Coulomb interaction within the LDA+U scheme.Results of the charge density and electron localization function distribution indicate that CeO2is an insulator with covalent bonding between Ce and O atoms.Calculated dielectric constants，Born effective charge tensors，phonon dispersion curves reproduce the experimental data reasonably.

electronic structure，optical properties，lattice dynamics，first-principles calculation

book=172,ebook=172

*國家自然科學基金(批準號:50730004和50802089)，浙江省“錢江人才計劃”(批準號:2007R10028)，教育部留學回國基金(批準號:［2008］890)和浙江省自然科學基金(批準號:Y407188和Y4090280)資助的課題.

?通訊聯系人.E-mail:siqishihz@gmail.com