緊支撐正交多小波的構(gòu)造

李萬社，羅立娑，鄭李娥

（陜西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院，陜西 西安 710062）

緊支撐正交多小波的構(gòu)造

李萬社，羅立娑，鄭李娥

（陜西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院，陜西 西安 710062）

通過選取初等旋轉(zhuǎn)矩陣和初等反射矩陣，利用多分辨分析以及矩陣理論，給出了一種由已知緊支撐對稱正交多小波構(gòu)造具有相應(yīng)性質(zhì)多小波的方法.利用該方法還可以構(gòu)造出一類平衡小波.最后，結(jié)合DGHM緊支撐對稱正交多小波給出了具體的算例.

多小波；多濾波器組；對稱性；正交性

0 引 言

小波理論發(fā)展非常迅速，人們可以根據(jù)不同需要構(gòu)造出不同的小波[1].1988年，Daubechies[2]指出：對于2帶小波，除了Haar小波外，不存在任何正交、對稱且緊支撐的小波，并且給出了相應(yīng)的證明.相對單小波而言，多小波能同時具有對稱性、正交性、緊支撐性和高階消失矩等性質(zhì)，所以，多小波成為小波研究的新熱點.1996年，Chui和Lian利用對稱性給出了2重多尺度函數(shù)和多小波函數(shù)，后來又有更多的人對多小波的理論體系作了研究[3-10]，這使多小波在理論應(yīng)用上趨于成熟.Jiang[4]給出了多帶多小波的參數(shù)化形式，楊守志等人[5-8]給出了幾種多小波的構(gòu)造方法，Lebrun等人[3，9-10]分別對多小波預(yù)濾波和平衡處理作了研究.還有更多的文獻對多小波的構(gòu)造和性質(zhì)做了深入的研究.本文根據(jù)已有文獻的研究，在給定一個緊支撐對稱正交多小波的基礎(chǔ)上，通過選取初等旋轉(zhuǎn)矩陣和初等反射矩陣[11]，與已知的緊支撐對稱正交多小波作乘積，構(gòu)造出相應(yīng)性質(zhì)的多小波.最后，本文構(gòu)造了相應(yīng)性質(zhì)的正交多小波.

1 預(yù)備知識

上式中r×r矩陣序列{Pk}k∈Z稱為兩尺度矩陣序列，Φ（x）稱為2尺度r重尺度函數(shù).對式

設(shè) Φ ＝ [φ1，…，φr]T， φ1，…，φr∈L2（R）滿足如下方程：

定義1 定義子空間序列Vj?L2（R）如下：

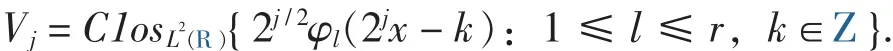
稱由式（1）定義的Φ（x）生成一個多分辨分析{Vj}j∈Z，若{Vj}j∈Z滿足：構(gòu)成 Vj的一個 Riesz基.

定義Wj⊕Vj=Vj+1，j∈Z，其中Wj是Vj在Vj+1中的正交補空間.向量函數(shù)Ψ（x）=[Ψ1，…，Ψr]T，Ψl∈L2（R），l=1，2，…，r的整數(shù)平移構(gòu)成 Wj的一個 Riesz基，即：

因為 Ψ1，…，Ψr∈W0?V1，所以存在 r× r矩陣序列{Qk}k∈Z滿足：

定義2[1]若存在正整數(shù)k1，k2（k1＜k2）使得當(dāng)k2＞k且k1＜k時， 有Pk=o，Qk=o，其中 o 是 r× r的零矩陣， 則由式（2）和（4）定義的濾波器組{P（z），Q（z）}稱為有限脈沖（FIR）多濾波器組， 同時也稱{Φ（x）,Ψ（x）}是緊支撐的.

引理1[1]若U是任意的正交矩陣，Φ（x）和Ψ（x）是多尺度函數(shù)和多小波，則仍然是正交的多尺度函數(shù)和多小波.

2 緊支撐對稱正交多小波的構(gòu)造

引理2[11]令正交矩陣

其中c=cos θ，s=sin θ，Ri,j表示除第i列和第j列外其余列都是單位基向量.矩陣中沒有寫出的元素都是零元素.這樣的矩陣稱為 Givens 矩陣， 并記 Ri，j=Ri，j（c，s）.

定理 1 若 Φ =[φ1，…，φr]T， Ψ（x）＝ [Ψ1，…，Ψr]T是緊支撐對稱正交多小波所對應(yīng)的多尺度函數(shù)和多小波函數(shù)， 構(gòu)造Φ1（x）和Ψ1（x）如下：

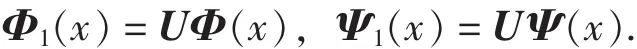
其中， U 是 Givens矩陣， 并且有 Φ1=[φ11，…，φ1r]T， Ψ1（x） ＝ [Ψ11,… ,Ψ1r]T， 則 Φ1（x）和Ψ1（x）分別是緊支撐對稱正交多小波的尺度函數(shù)和多小波函數(shù).

證明 因為Φ（x）和Ψ（x）是緊支撐對稱正交多小波所對應(yīng)的尺度函數(shù)和多小波函數(shù)，并且Givens矩陣是正交矩陣，所以由引理1可得，Φ1（x）和Ψ1（x）仍然是緊支撐對稱正交多尺度函數(shù)和多小波函數(shù).

定理 2 若{P1（z），Q1（z）}是定理 1 中所構(gòu)造的 r重緊支撐對稱正交多小波{Φ1（x），Ψ1（x）}的 FIR 濾波器組， {P（z），Q（z）}是{Φ（x），Ψ（x）}的濾波器組， 則有：

其中，

證明 由 Φ（x） =U-1Φ1（x）可得： Φ（2x-k） =U-1Φ1（ 2x-k ）.由式（1）可得：

所以， P1（z） =UP（z）U-1.同理可得：Q1（z） =UQ（z）U-1.從而有：

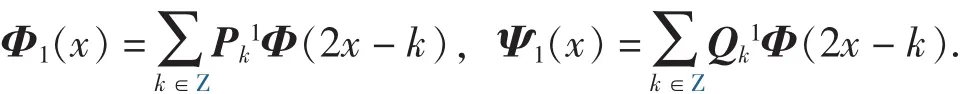
命題得證.

定理3 條件同定理1，設(shè)Φ1（x）和Ψ1（x）是定理1中所構(gòu)造的多尺度函數(shù)和多小波函數(shù)，則有：

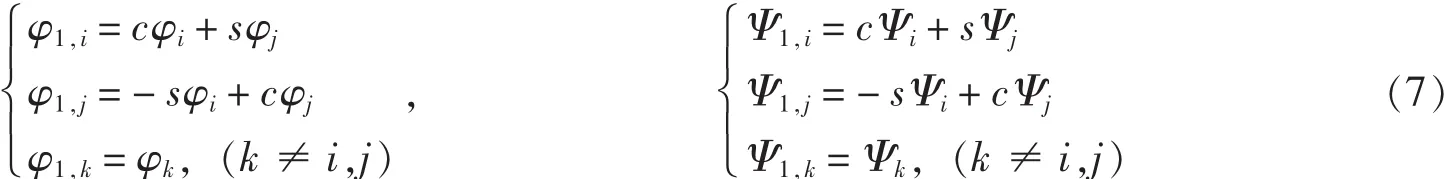
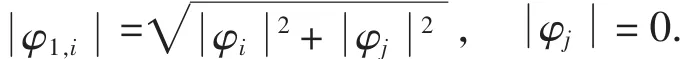
下面借助初等反射矩陣構(gòu)造多尺度函數(shù)和多小波函數(shù).

定義3[11]一般地，在Rn中，可以定義關(guān)于 “法線為單位向量u的n-1維子空間”對稱的變換.設(shè)單位向量u∈Rn，稱H=I-2uuT為Householder矩陣（或者初等反射矩陣）.由初等反射矩陣確定的變換稱為初等反射變換.

引理3[11]Householder矩陣是對稱矩陣，即HT=H；是正交矩陣，即HTH=I；是自逆矩陣，即H-1=H；是對合矩陣，即H2=H；行列式為-1，即det H=-1.

引理4[11]初等旋轉(zhuǎn)矩陣是兩個初等反射矩陣的乘積.

定理 4 若 Φ =[φ1，…，φr]T，Ψ（x）＝[Ψ1,… ,Ψr]T是緊支撐對稱正交多小波所對應(yīng)的多尺度函數(shù)和多小波函數(shù)， 構(gòu)造 Φ2（x） ,Φ3（x）和 Ψ2（x），Ψ3（x）如下：

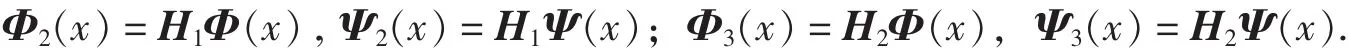
其中Householder矩陣H1,H2如下：

令H1中θ為3θ便得H2=I-2vvT，并且有：

Φ2=[φ21，…，φ2r]T， Ψ2（x） ＝ [Ψ21，…，Ψ2r]T； Φ3=[φ31，…，φ3r]T， Ψ3（x） ＝ [Ψ31，…，Ψ3r]T.則 Φ2（x），Φ3（x）和 Ψ2（x），Ψ3（x）分別是緊支撐對稱正交多小波的尺度函數(shù)和多小波函數(shù).

定理 5 Φ1（x），Φ2（x），Φ3（x）和 Ψ1（x），Ψ2（x），Ψ3（x）如前面定理所構(gòu)造， 則：

由上面的構(gòu)造過程可以看出，根據(jù)初等旋轉(zhuǎn)矩陣和初等反射矩陣的性質(zhì)以及引理1，構(gòu)造出了一系列相關(guān)的多尺度函數(shù)和多小波函數(shù).

定理 6 Φ1（x） ,Φ2（x） ,Φ3（x）和 Ψ1（x） ,Ψ2（x） ,Ψ3（x）如前面定理所構(gòu)造， 則：

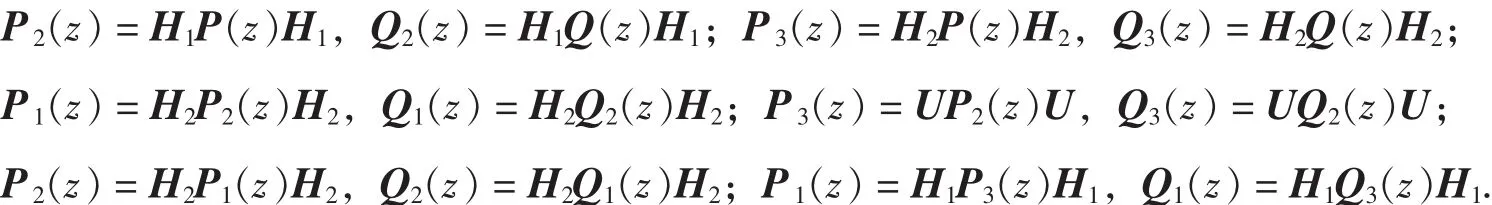
推論 CL2多小波[1]的一階正交平衡器是定理1中Givens矩陣參數(shù)θ＝π/4時的結(jié)果.

注[2]在多小波的平衡理論中，這是一個很特殊的平衡器，它對原小波基作了π/4角度的旋轉(zhuǎn)，多數(shù)多小波都可以通過它來達到一階平衡.

3 算 例

已知具有2階消失矩支集長度是4的對稱正交多小波DGHM濾波器系數(shù)如下：

其中多小波基 Φ =[φ1，φ2]T是緊支撐的， 并且 supp φ1=[0，1]， supp φ2=[0，3]， 由式（2）：

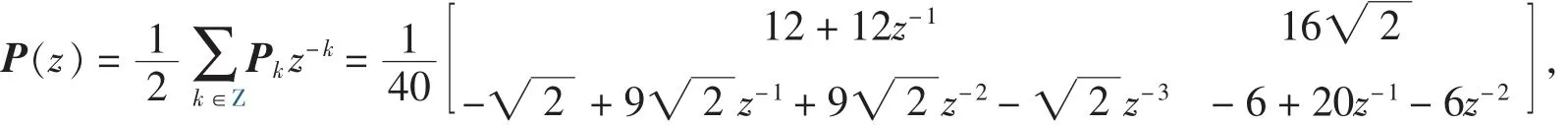
其中，

由式（4）可得：

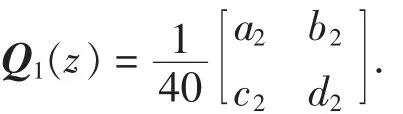
其中，

以上所得到的{P1（z），Q1（z） }即為所構(gòu)造的與{P（z），Q（z）}具有相同性質(zhì)的多小波的濾波器組，其中參數(shù)θ可以根據(jù)需要來確定，從而得出不同的結(jié)果.特別地，取θ=ω/4就得到了CL2多小波的一階正交平衡器，使DGHM滿足一階平衡.

[1]唐遠炎，王玲.小波分析與文本文字識別[M].北京：科學(xué)出版社，2004.

[2]Daubechies I.小波十講[M].李建平，楊萬年，譯.北京：國防工業(yè)出版社，2004.

[3]Lebrun J， Vetterli M.Balanced multiwavelets theory and design[J].IEEE Trans on Signal Processing，1998， 46（4）： 1 119-1 125.

[4]Jiang Q T.Parameterization of m-channel orthogonal multifilter banks[J].Advances in Computational Mathematics， 2000， 12： 189-211.

[5]楊守志，唐遠炎，程正興.a尺度緊支撐正交多小波的構(gòu)造[J].計算數(shù)學(xué)，2002，24（4）：451-461.

[6]崔麗鴻，程正興.多小波與平衡多小波的理論和設(shè)計[J].工程數(shù)學(xué)學(xué)報，2001，18（5）：105-116.

[7]全宏躍，王國秋.一類對稱正交多小波的構(gòu)造[J].應(yīng)用數(shù)學(xué)學(xué)報，2008，31（4）：682-691.

[8]Chui C K， Lian J A.A study of orthogonal multi-wavelets[J].Appl Numer Math， 1996， 20（3）：273-298.

[9]Lebrun J，Vetterli M.High order balanced multiwavelets[C]. In Proc IEEE int Conf Acoust Speech Signal Proce（ICASSP）， 1998： 12-15.

[10]Lebrun J，Vetterli M.Balanced multiwavelets[C]. In Proc IEEE int Conf Acoust Speech Signal Proce（ICASSP）， 1997， 3： 2 473-2 476.

[11]胡茂林.矩陣計算與應(yīng)用[M].北京：科學(xué)出版社，2008.

Abstract：In this paper,a method is given to generate a new multi-wavelet with the corresponding properties from a compactly supported symmetric orthonormal multi-wavelet by choosing elementary rotation matrix and elementary reflection matrix. A class of balanced wavelets can also be constructed using this method. At last，the DGHMcompactly supported symmetric orthogonal multi-wavelet is given in the method as an example.

Key words：multi-wavelet； multi-filter bank； symmetric； orthonormal

Construction of Compactly Supported Orthonormal Multi-Wavelet

LI Wan-she， LUO Li-suo， ZHENG Li-e
（College of Mathematics and Information Science， Shaanxi Normal University， Xi’an 710062， Shaanxi， China）

O 174.2

A

1001-4217（2010）04-0026-07

2010-06-02

李萬社（1963-），男，陜西西安人，教授.研究方向：智能信號處理.E-mail：liwsh@snnu.edu.cn

國家自然科學(xué)基金資助項目（10571113）.