基于改進遺傳算法的煤礦探測機器人路徑規劃

周 巍,李元宗

(太原理工大學機械工程學院,太原030024)

我國是煤炭資源大國,也是世界上最大的煤炭生產國和消費國。然而,由于礦井自然條件差,高瓦斯礦井多,隨著近年來國家對煤炭資源需求量的不斷增長,使得煤礦開采中瓦斯爆炸、涌水、著火等事故頻繁發生,由此造成重大的人員傷亡事故和不良的社會影響,嚴重制約著煤炭工業的健康發展。因此,研發煤礦探測機器人是煤礦井下發生瓦斯爆炸事故后進行搶險救援的前提手段和必要工具,對煤礦安全生產、減少國家和人民生命財產的損失具有十分重要的意義。本課題的研究得到了山西省科技攻關項目的資助,其中煤礦井下搜救探測機器人運動裝置已獲得國家發明專利。

煤礦巷道本身是一個非常復雜的三維非結構化環境,特別是礦難發生后,原有結構往往遭到不同程度的破壞。煤礦探測機器人置身于這種復雜環境,必須具有一定的路徑規劃能力,即能夠在有障礙物的工作環境內,尋找一條從起始位置到達目標位置的無碰路徑,同時還要保證這是一條按照路徑長度最短、能量消耗最少、使用時間最短等優化準則產生的最優路徑。目前,求解機器人路徑規劃的方法有很多,與傳統優化方法相比,遺傳算法以其較強的全局優化能力和較高的搜索效率在解決此類問題中得到廣泛的應用[1-6]。但是,以上方法仍然存在許多不足,如早熟現象、接近最優解時收斂較慢等[7],這將可能導致局部最優解的產生,并影響到在實時性要求較高的環境中的應用。筆者根據煤礦探測機器人路徑規劃本身的實際應用要求,結合遺傳算法所具有的特點,對傳統的遺傳算法進行了改進：在機器人工作的復雜三維空間中,充分考慮到井下環境地形的高低變化,采用柵格法對其進行建模,并根據路徑長度最短、能耗最少的評價指標設計了適應度函數。按照可變長度的染色體編碼方式及隨機指導式搜索策略來生成初始種群,保證初始階段無障礙路徑的產生。同時,針對傳統遺傳算法中存在的“早熟現象”和“收斂速度慢”等問題,將交叉算子和變異算子進行優化設計,從而使整個規劃過程變得簡單而有效。

1 規劃空間的建模

路徑規劃算法所處理的空間是環境的抽象空間,而機器人的工作空間是一個現實的物理空間,所以建立環境模型即實現物理空間到抽象空間的映射是進行機器人路徑規劃的一個重要環節。煤礦探測機器人工作的空間為三維地形空間,其中任意一點的坐標可表示為(x,y,z),其中平面 xy采用由Howden W.E.提出的柵格法[8]進行劃分,以柵格為單位記錄環境平面信息,z值則表示高度信息。這樣工作空間被量化成具有一定分辨率的柵格,柵格的大小以機器人自身的尺寸為準,直接影響著環境信息存儲量的大小和規劃時間的長短。柵格劃分太大,環境信息存儲量小,規劃時間短,但分辨率會下降,路徑規劃不夠精確;柵格劃分太小,環境分辨率提高了,但環境信息存儲量加大,規劃時間長。因此,可以通過比較機器人、障礙物及工作空間的大小來確定柵格的尺寸與數目,既保證機器人能在工作空間中靈活運動,又盡可能地減少環境信息的存儲量,縮短機器人進行路徑規劃的時間。

假設機器人工作在具有靜態障礙物的環境空間中,障礙物的位置和大小已知,把障礙物邊界向外擴展一個最小安全距離即機器人本體在長、寬方向上最大尺寸的1/2,這樣機器人就可看作為一個質點。劃分后的機器人工作空間如圖1所示,自由空間和障礙物均可表示為柵格的集成。圖1中,黑色區域表示障礙柵格;柵格內不含任何障礙物,則為自由柵格,用白色區域表示。柵格內的數字表示離散化后的高度信息[9]。

圖1 機器人的工作空間

本文采用直角坐標法和序號法兩種柵格的標識方法。

1)直角坐標法。在圖1中,柵格圖的左上角為坐標原點,X軸、Y軸的正方向分別為水平向右和垂直向下,坐標軸上的單位長度定義為柵格區間的大小,則任意柵格均可由其直角坐標(x,y)惟一確定。

2)序號法。在圖1中,定義左上角第一個柵格序號為0,并按照從左到右、從上到下的次序柵格序號依次遞增的方法,為每個柵格定義一個序號 N,則每個柵格與其序號一一對應。

上述兩種表示方法具有如下對應關系：

其中,mod表示取N/10之余數,int表示取N/10之整數。

在下面的算法分析中,分別用到了這兩種柵格標識法。其中,序號法用于機器人運動路徑的表示,因為序號法表示簡單直觀,便于進行遺傳操作,且比直角坐標法節省內存。而在規劃路徑評價時,為了便于計算路徑長度,則依照上述對應關系將序號轉換成直角坐標。

2 基于改進遺傳算法的路徑規劃方法

2.1 染色體的編碼方式

遺傳算法的運算對象是表示染色體的符號串,染色體表示機器人在工作空間中的一條運動路徑。由于機器人運動路徑可變,為了直觀地表示生成的各條路徑,方便遺傳算子的操作,文中采用可變長度的染色體編碼方式,用序號法標識柵格,從起始位置到終點位置由不同柵格序號連接起來的符號串即可描述一條路徑。如圖2所示,若設起點為0,終點為99,則圖中所示的一條可行路徑可以用符號串(0,10,21,31,42,52,53,64,65,76,77,78,88,98,99)加以描述。

2.2 初始種群的生成

遺傳算法是對群體進行的進化操作,種群初始化是迭代運算的起點。為了保證算法能達到全局最優,初始種群應盡可能隨機分布在搜索空間中每一個區域。若采用隨機生成法,雖然能保持生成路徑的多樣性,但生成可行解的效率較低,因此本文用一系列隨機生成與自由柵格構成的路徑連接起點和終點,產生一條無障礙路徑,有效地保證了生成路徑的可行性,減少了初始種群產生的困難和盲目性。

2.3 適應度函數的設計

遺傳算法中以適應度函數表明個體的優劣程度,從而決定其遺傳機會的大小,直接影響到遺傳算法的計算效率。結合實際情況,本文以路徑長度和能量消耗作為評價指標,目標是找到這樣一條路徑：從起點到達終點的距離即路徑長度最短,同時從起點到達終點的能耗也是最少的。因此個體適應度函數構造為

式中：α,β為權重系數,分別表示不同評價指標所占權重。令

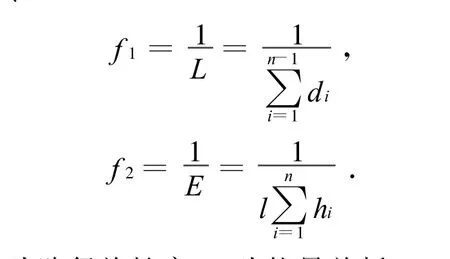
式中：L為路徑總長度;E為能量總耗;d i表示路徑中相鄰兩點的距離;hi表示路徑中第i個柵格的高度;l表示柵格區間的大小。

2.4 遺傳算子的操作

2.4.1 選擇算子

選擇操作采用De Jong K.A.提出的最優保存策略,也稱為“精英保留”策略。其思想是把當前種群中適應度最高的個體完整地復制到下一代,并將下一代種群中適應度最小的個體淘汰,下一代種群中其余的個體則由輪盤賭選擇法產生[10]。該策略的采用可以保證遺傳算法迄今為止得到的最優個體不會因交叉、變異等遺傳運算而破壞,它是遺傳算法收斂性的一個重要保證,同時從理論上可以證明采用“精英保留”策略的標準遺傳算法是全局收斂的[11]。

2.4.2 交叉算子

交叉操作是通過把兩個父代個體的部分基因相互交換重組而生成兩個新個體的操作,是遺傳算法區別于其他進化算法的重要特征。本文采用單點和重合點混合的交叉方式。所謂重合點交叉是指對隨機選取的兩個個體,選擇柵格序號完全相同的點進行交叉操作,當重合點多于一個時,隨機選擇其一進行交叉。若沒有重合點,則隨機選擇交叉點進行單點交叉。顯然常規交叉操作易產生間斷路徑,而重合點交叉不會產生新的斷點。

2.4.3 變異算子

變異操作在改善局部搜索能力和維持種群多樣性,防止出現早熟現象方面起著關鍵的作用。在傳統遺傳算法中采用的是隨機變異操作,并沒有對已知的環境信息加以利用,于是變異常常導致路徑劣化。為此,筆者采用改進型變異算子,利用局部啟發式搜索技術,保證變異后的節點必須在待變異節點相鄰的自由區域內,且在路徑的前進方向上,從而避免了變異的盲目性,以此來提高變異后生成新路徑的連通性及算法的收斂性。

2.5 算法終止條件

本文采用遺傳算法中常用的規定進化代數和設定收斂條件相結合的復合準則。當遺傳算法滿足設定的收斂判斷條件時,算法終止;若達到規定進化代數但仍未滿足設定的收斂判斷條件,算法也將終止。其中設定算法的收斂條件為：若連續進化五代后,最優解均未發生變化,且適應度函數值提高不足1%。

3 仿真實驗結果

遺傳算法中運行參數的選擇非常關鍵,控制參數的不同選取會對算法收斂性和最終解的質量產生直接影響。考慮到本文在初始種群生成時已采取一定的優化措施,因此,種群規模可取較小值,M=30;規定終止進化代數G=50。由于在交叉、變異等遺傳算子的設計中,采取一系列的措施保證了產生的個體路徑的有效性,所以交叉概率p c和變異概率pm的取值較大(其中pc=0.9,pm=0.1),以提高算法的全局搜索能力。

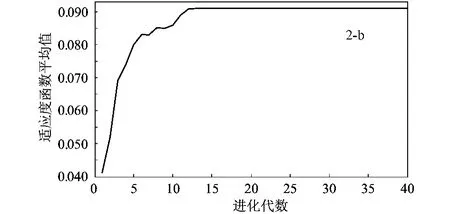
圖2 改進遺傳算法的仿真結果

為了研究改進遺傳算法的正確性和有效性,并與采用單點交叉和隨機變異的傳統遺傳算法進行比較,本文在10×10柵格的規劃空間進行了仿真實驗,結果如圖2、圖3所示。圖中S和G分別表示機器人運動路徑的起點和終點,折線表示算法所產生的最優路徑。圖2-a、圖3-a分別表示改進遺傳算法和傳統遺傳算法找到的最優路徑,圖2-b、圖3-b分別表示改進后和改進前的群體適應度函數平均值隨著進化代數的收斂情況。圖中結果顯示,采用筆者提出的改進遺傳算法,進化約進行了12代后已達到收斂,而傳統遺傳算法則需要進化17代,說明改進算法具有很高的收斂速度。

圖3 傳統遺傳算法的仿真結果

另外,本文還對隨機運行60次的實驗結果進行統計,從最小成功收斂代數、平均收斂代數及最優解出現概率等方面對算法的性能進行比較,結果如表1所示。

表1 算法的性能比較

可以看出,改進后的遺傳算法較改進前在收斂性能和搜索效率上都有很大提高。

4 結束語

筆者針對煤礦探測機器人的實際應用要求,在三維空間中對機器人工作環境進行建模,采用了可變長度的染色體編碼方式,使用隨機指導式搜索策略來生成初始種群,保證初始階段無障礙路徑的產生,降低了算法的復雜性。根據路徑長度最短且能耗最少的評價指標設計了適應度函數,有效地利用了路徑規劃中的地圖信息。對遺傳算法中的交叉和變異算子的優化設計,解決了傳統遺傳算法“早熟現象”和“收斂速度慢”的問題。仿真實驗證明了本文所提算法的有效性和可行性,后續的主要工作是結合煤礦探測機器人的工作情況,將改進的算法應用到實際當中,并對提高算法的效率和收斂速度進行進一步的研究。

[1] 孫樹棟,曲彥賓.遺傳算法在機器人路徑規劃中的應用研究[J].西北工業大學學報,1998,16(1)：79-83.

[2] GERKE M.Genetic path planning for mobile robots[C]∥IEEE.Proceedings of the 1999 American Control Conference.San Diego ：IEEE Press,1999 ：2424-2429.

[3] Hu Y,Yang S X.A knowledge based genetic algorithm for path p lanning of a mobile robot[C]∥IEEE.Proceedings of the 2004 IEEE international Conference on Robotics and Automation.New Orleans：IEEE Press,2004：4350-4355.

[4] 王強,姚進,王進戈.基于遺傳算法的移動機器人的一種路徑規劃方法[J].哈爾濱工業大學學報,2004,36(7)：867-870.

[5] TU J,YANG S.Genetic algorithm based path planning for a mobile robot[C]∥IEEE.Proceedings of the 2003 IEEE International Conference on Robotics and Automation.Taipei：IEEE Press,2003 ：1221-1226.

[6] OSCA RCastillo,LEONA RDO Trujillo.Multiple objective genetic algorithms for path planning optimization in autonomous mobile robots[J].Soft Computing,2007,11(1)：269-279.

[7] 雷英杰,張善文,李續武,等.MATLAB遺傳算法工具箱及應用[M].西安：西安電子科技大學出版社,2005.

[8] HOWDEN W.E.The sofa p roblem[J].The Computer Journal,1968,11(3)：299-301.

[9] 師黎,邵國.改進遺傳算法用于移動機器人路徑規劃[J].計算機工程與設計,2008,29(24)：6330-6333.

[10] DE JONG K A.An analysis of the behavior of a class of genetic adaptive systems[D].Michigan：University of Michigan,1975.

[11] RUDOLPH G.Convergence analysis of canonical genetic algorithms[J].IEEE Trans on Neural Networks,1994,5(1)：96-101.