空對(duì)空單站被動(dòng)跟蹤體制與精度仿真分析
彭 峰,李 騰,鄧新蒲
(國(guó)防科學(xué)技術(shù)大學(xué) 電子科學(xué)與工程學(xué)院,湖南 長(zhǎng)沙 410073)
0 引言
現(xiàn)代高技術(shù)戰(zhàn)爭(zhēng)中,制空能力是贏得戰(zhàn)爭(zhēng)的重要保證。采用機(jī)載單平臺(tái)的無(wú)源定位跟蹤技術(shù),可先發(fā)制敵,消除空中威脅,提高戰(zhàn)機(jī)的空中生存能力。
與角度相位差變化率、角度頻率變化率相比,在單站空對(duì)空應(yīng)用中BO的優(yōu)點(diǎn)是測(cè)量設(shè)備較簡(jiǎn)單,只需測(cè)向即可定位,對(duì)信號(hào)波形、頻率的捷變不敏感;缺點(diǎn)是為滿足定位的可觀測(cè)性,對(duì)運(yùn)動(dòng)的輻射源進(jìn)行跟蹤需觀測(cè)器自身作機(jī)動(dòng);定位精度對(duì)方向測(cè)量誤差非常敏感,要求設(shè)備的測(cè)向精度高[1]。與BO相比,角度相位差變化率定位體制的定位精度略有提高,定位收斂速度較快。但測(cè)量參數(shù)較多、系統(tǒng)較復(fù)雜、可觀測(cè)性與BO相同。與BO和角度相位差變化率相比,角度頻率變化率定位體制的定位收斂速度較快,提高了可觀測(cè)性,對(duì)勻速運(yùn)動(dòng)的目標(biāo)定位無(wú)需觀測(cè)站機(jī)動(dòng),但測(cè)量的參數(shù)較多,系統(tǒng)較復(fù)雜,要求的頻率變化率測(cè)量精度達(dá)到每秒赫茲量級(jí),頻率變化率精度受信號(hào)形式的影響[2]。為此,本文以空中運(yùn)動(dòng)單平臺(tái)對(duì)空中運(yùn)動(dòng)目標(biāo)被動(dòng)定位跟蹤為研究對(duì)象,比較了BO、角度相位差變化率和角度頻率變化率三種典型定位跟蹤體制,分析了測(cè)量精度對(duì)跟蹤效果的影響,以及實(shí)際工程可得的測(cè)量精度和各定位體制適用條件。
1 模型與算法
1.1 狀態(tài)模型
空中運(yùn)動(dòng)輻射源與單觀測(cè)器如圖1所示。設(shè)地理坐標(biāo)系中,輻射源狀態(tài)矢量為(XT(xT,yT,zT,))T,觀測(cè)器狀態(tài)矢量為(Xo(xo,yo,zo,))T,則相對(duì)狀態(tài)矢量
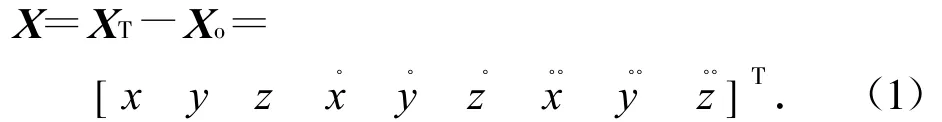
設(shè)觀測(cè)器與輻射源連線方向與干涉儀基線方向的夾角為α,觀測(cè)器采用基線長(zhǎng)度為d的二單元天線測(cè)量輻射源信號(hào)的相位差變化率和頻率變化率。
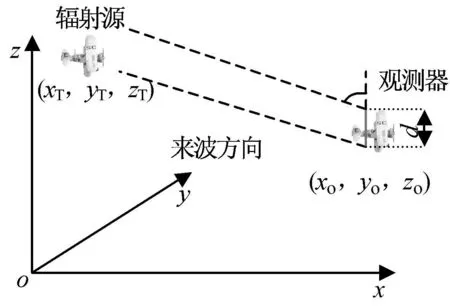
圖1 觀測(cè)站與輻射源Fig.1 Observer and emitter
在直角坐標(biāo)系統(tǒng)某坐標(biāo)方向上,目標(biāo)運(yùn)動(dòng)的數(shù)學(xué)模型可用列差分方程描述為
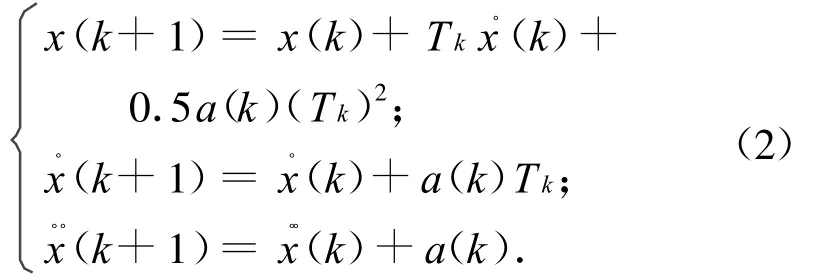
式中:Tk=tk-tk-1為第k-1、k次觀測(cè)間的時(shí)間間隔;a(k)為目標(biāo)加速度。則式(2)可用狀態(tài)方程表示為
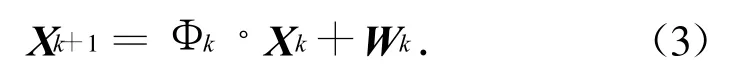
式中:Wk為狀態(tài)噪聲[3]。
1.2 測(cè)量模型
1.2.1 測(cè)量方程
定義β:輻射源與觀測(cè)器連線方向在平面xoy的投影與ox軸正向間的夾角,順時(shí)針?lè)较驗(yàn)檎?有
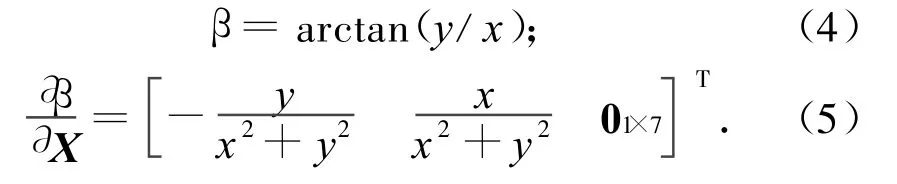
1.2.2 測(cè)量方程
定義ε:輻射源與觀測(cè)器連線方向與oz軸正向的夾角。有
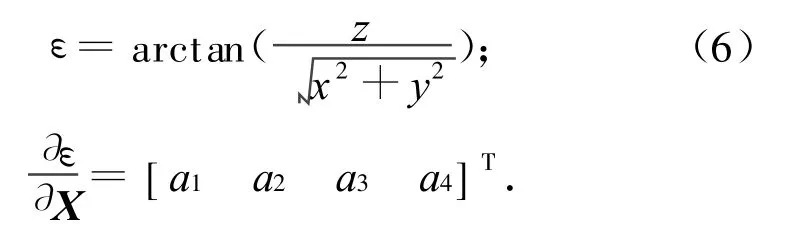
式中:a1=-;a2=-;a3=;a4=01×6。此處:r為輻射源與觀測(cè)器間的距離,且r=。

二單元天線測(cè)得的相位差φ可表示為
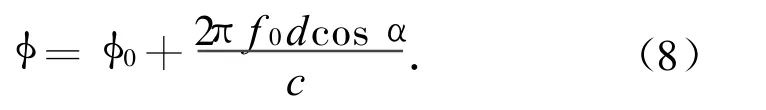
式中:φ0為兩天線通道固定相位差;f0為載波頻率;c為光速;α為觀測(cè)器與輻射源連線方向與干涉儀基線方向的夾角[4]。令,則測(cè)量方程為
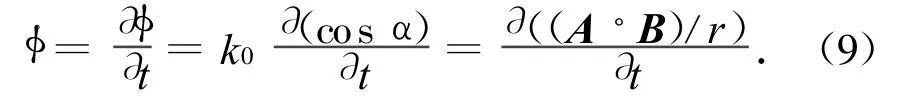
式中:A=[x y z];B為地理坐標(biāo)系中干涉儀基線方向的單位矢量,且B=[b1b2b3]T。令ξ=,則
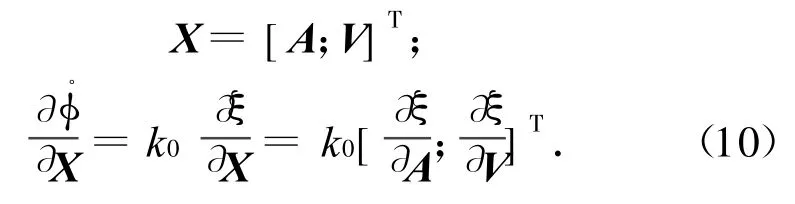
式中:
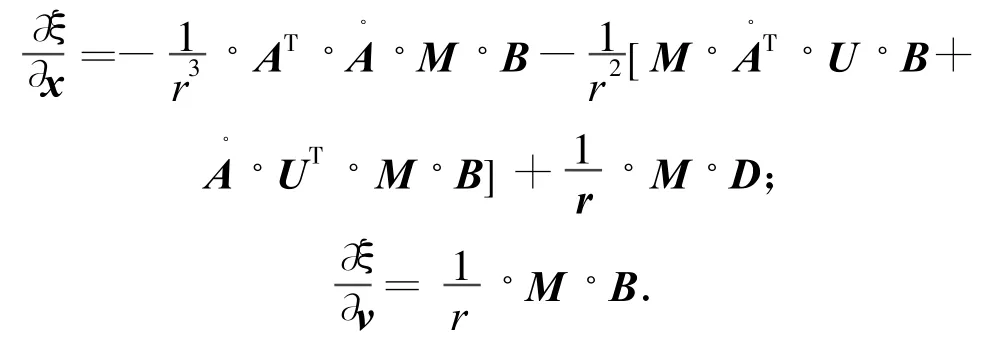
1.3 濾波算法
根據(jù)不同的跟蹤體制,可用不同的測(cè)量參數(shù)組合進(jìn)行跟蹤濾波。EKF算法濾波過(guò)程為:
步驟1,預(yù)測(cè)
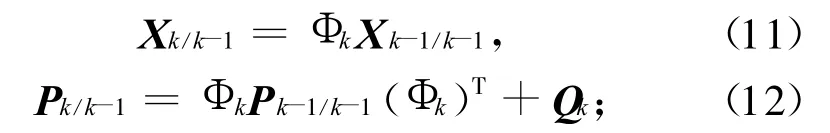
步驟2,雅可比矩陣計(jì)算

步驟3,增益計(jì)算
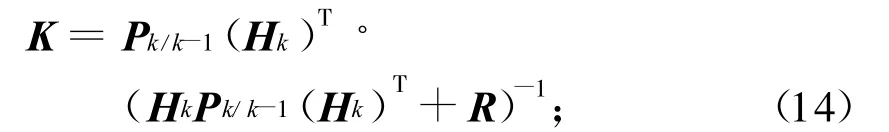
步驟4:濾波更新
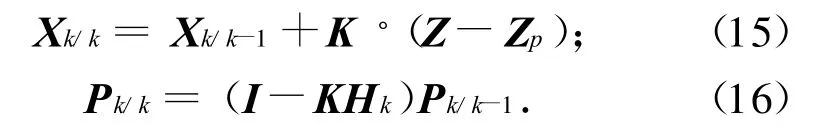
式中:Qk為狀態(tài)誤差方差陣;Z為目標(biāo)觀測(cè)值;Zp為目標(biāo)預(yù)測(cè)的當(dāng)前值;f(X)為測(cè)量量關(guān)于X的函數(shù);R為測(cè)量誤差方差陣[3]。
相關(guān)測(cè)量參數(shù)對(duì)狀態(tài)變量導(dǎo)數(shù)的向量組合成相應(yīng)的雅可比陣:BO體制對(duì)應(yīng)的測(cè)量量為β,ε;角度相位差變化率體制對(duì)應(yīng)的測(cè)量量為β,ε,;角度頻率變化率體制對(duì)應(yīng)的測(cè)量量為β,ε,。三種體制的EKF算法雅可比陣相應(yīng)為
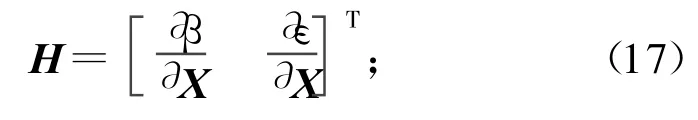

2 仿真
設(shè)觀測(cè)器初始位置為經(jīng)緯度(118.3°,24.2°),高度10 km,初始速度[0 300 0]m/s;輻射源初始位置為經(jīng)緯度(119.5°,24.3°),高度10 km,初始速度[-300 0 0]m/s;觀測(cè)器與輻射源的初始徑向距離約120 km,仿真時(shí)間200 s。用蒙特卡羅法仿真50次。
2.1 典型測(cè)量精度的定位體制跟蹤效果
設(shè)參數(shù)的測(cè)量精度為:角度測(cè)量精度約1°,相位差變化率測(cè)量精度約10(°)/s,頻率變化率測(cè)量精度約10 Hz/s。取導(dǎo)航誤差:位置誤差100 m,速度誤差1m/s,姿態(tài)誤差(方位角,俯仰角,橫滾角)0.2°。不同運(yùn)動(dòng)狀態(tài)時(shí)定位體制的徑向距離相對(duì)誤差如圖2所示。
由圖2(a)可知:當(dāng)觀測(cè)器和輻射源均勻速直線運(yùn)動(dòng)時(shí),角度頻率變化率體制在80 s時(shí)徑向距離相對(duì)誤差收斂至約5%,BO和角度相位差變化率體制不收斂。由圖2(b)可知:當(dāng)觀測(cè)器勻加速運(yùn)動(dòng)、輻射源勻速運(yùn)動(dòng)時(shí),徑向距離相對(duì)誤差收斂為約5%,BO體制需72 s,角度相位差變化率體制需33 s,角度頻率變化率體制需69 s。由圖2(c)可知:當(dāng)觀測(cè)器圓周運(yùn)動(dòng)、輻射源勻速運(yùn)動(dòng)時(shí),徑向距離相對(duì)誤差收斂至約5%,BO體制需68 s,角度相位差變化率體制需45 s,角度頻率變化率體制需48.5 s。由圖2(d)可知:當(dāng)觀測(cè)器圓周運(yùn)動(dòng)、輻射源勻加速運(yùn)動(dòng)時(shí),徑向距離相對(duì)誤差收斂為約5%,BO體制需155 s,角度相位差變化率體制需44 s,角度頻率變化率體制需48 s。由此可見,與BO和角度相位差變化率體制相比,角度頻率變化率體制提高了可觀測(cè)性,對(duì)輻射源勻速運(yùn)動(dòng),觀測(cè)器勻速運(yùn)動(dòng)即可跟蹤。與BO體制相比,角度相位差變化率和角度頻率變化率體制因引入了新的信息量,收斂速度快,跟蹤效果較優(yōu)。
2.2 不同體制測(cè)量精度
設(shè)觀測(cè)器作圓周運(yùn)動(dòng),圓周半徑5 km;輻射源勻速運(yùn)動(dòng)。觀測(cè)器、輻射源初始位置、速度,以及導(dǎo)航誤差不變。比較參數(shù)測(cè)量精度對(duì)不同體制跟蹤效果的影響。
在角度測(cè)量精度分別為0.5°,1.0°,2.0°條件下,BO體制的徑向距離相對(duì)誤差如圖3所示。
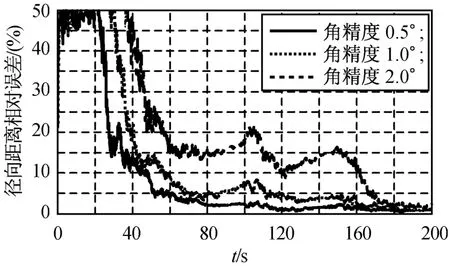
圖3 不同測(cè)角精度時(shí)BO的徑向距離相對(duì)誤差Fig.3 Tracking effect of BO with different angle precision
由圖3可知:角度測(cè)量精度為0.5°時(shí),徑向距離相對(duì)誤差在60 s時(shí)收斂至約5%;角度測(cè)量精度為1.0°時(shí),徑向距離相對(duì)誤差在115 s時(shí)收斂至約5%;角度測(cè)量精度為2.0°時(shí),徑向距離相對(duì)誤差在167 s時(shí)收斂至約5%。
在相同角度測(cè)量精度條件下,角度相位差變化率定位的徑向距離相對(duì)誤差圖4所示。
由圖4(a)可知:角度測(cè)量精度分別為0.5°,1.0°,2.0°時(shí),徑向距離相對(duì)誤差相應(yīng)在在38,44,45 s時(shí)收斂至約5%。由圖4(b)可知:相位差變化率精度分別為3,10,20(°)/s時(shí),徑向距離相對(duì)誤差相應(yīng)在43,46,50 s時(shí)收斂至約5%。
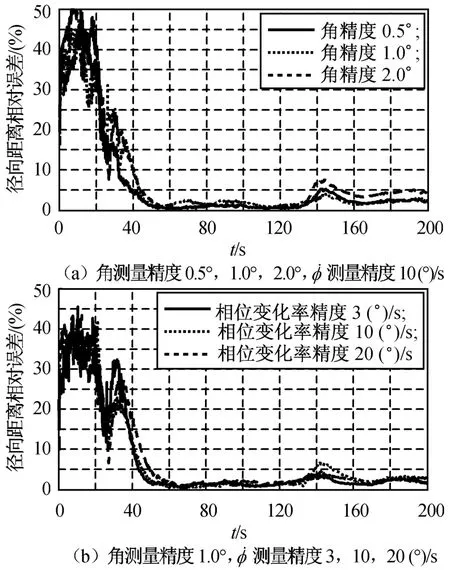
圖4 角度相位差變化率定位的測(cè)量精度Fig.4 Tracking effect by angle and phase difference rateprecision
在角度測(cè)量精度相同條件下,角度頻率變化率定位體制的徑向距離相對(duì)誤差如圖5所示。
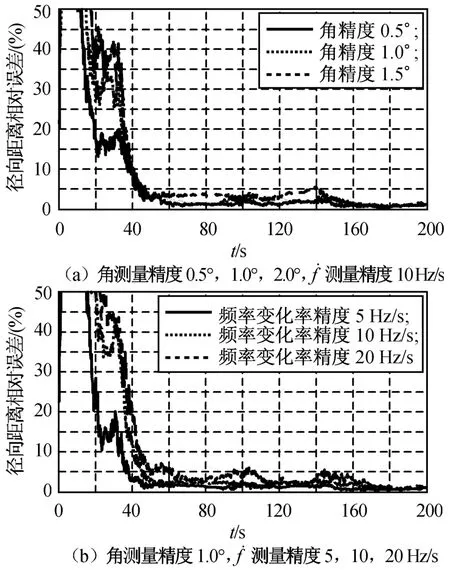
圖5 角度頻率變化率定位體制下測(cè)量精度變化對(duì)跟蹤效果影響Fig.5 Tracking effect by angleand frequency rateprecision
由圖5(a)可知:角度測(cè)量精度分別為0.5°,1.0°,2.0°時(shí),徑向距離相對(duì)誤差分別在43.8,45.0,45.0 s時(shí)收斂至約5%,跟蹤效果幾乎沒(méi)有影響。由圖5(b)可知:頻率變化率測(cè)量精度分別為5,10,20 Hz/s時(shí),徑向距離相對(duì)誤差相應(yīng)在38.2,46.0,60.0 s時(shí)收斂至約5%。
3 結(jié)束語(yǔ)
本文對(duì)空中運(yùn)動(dòng)單平臺(tái)對(duì)空中運(yùn)動(dòng)目標(biāo)被動(dòng)定位跟蹤,用仿真分析了BO、角度相位差和角度頻率變化率定位體制對(duì)跟蹤效果的影響。結(jié)果表明:角度頻率變化率體制的可觀測(cè)性優(yōu)于BO和角度相位差變化率體制,對(duì)輻射源勻速運(yùn)動(dòng),觀測(cè)器勻速運(yùn)動(dòng)即可跟蹤;與BO測(cè)角體制相比,角度相位差變化率和角度頻率變化率體制增加了觀測(cè)量,跟蹤收斂速度快。因此,可根據(jù)具體環(huán)境和實(shí)際參數(shù)測(cè)量精度選擇不同的跟蹤體制,實(shí)現(xiàn)快速高精度跟蹤。本文研究對(duì)空空作戰(zhàn)有一定的參考意義。
[1]單月暉,孫仲康,皇甫堪.單站無(wú)源定位跟蹤現(xiàn)有方法評(píng)述[J].航天電子對(duì)抗,2001(6):4-7.
[2]龔享銥.利用頻率變化率和波達(dá)角變化率單站無(wú)源定位與跟蹤的關(guān)鍵技術(shù)研究[D].長(zhǎng)沙:國(guó)防科學(xué)技術(shù)大學(xué),2004.
[3]劉福聲,羅鵬飛.統(tǒng)計(jì)信號(hào)處理[M].長(zhǎng)沙:國(guó)防科技大學(xué)出版社,1999.
[4]許耀偉.一種快速高精度無(wú)源定位方法的研究[D].長(zhǎng)沙:國(guó)防科學(xué)技術(shù)大學(xué),1998.

