基于計(jì)算機(jī)實(shí)測(cè)技術(shù)的音叉固有頻率測(cè)量
李定梅,甘奕文,封 玲
(深圳大學(xué)物理科學(xué)與技術(shù)學(xué)院,廣東深圳518000)
基于計(jì)算機(jī)實(shí)測(cè)技術(shù)的音叉固有頻率測(cè)量
李定梅,甘奕文,封 玲
(深圳大學(xué)物理科學(xué)與技術(shù)學(xué)院,廣東深圳518000)
采用計(jì)算機(jī)實(shí)測(cè)技術(shù)進(jìn)行音叉固有頻率的測(cè)量,并與教材上所采用的實(shí)驗(yàn)方法進(jìn)行比較.對(duì)比原方法,采用計(jì)算機(jī)實(shí)測(cè)技術(shù)進(jìn)行的測(cè)量更加直觀簡(jiǎn)便,結(jié)果也更準(zhǔn)確.
音叉;固有頻率;實(shí)時(shí)實(shí)測(cè)
音叉固有頻率的測(cè)量一般是在音叉帶動(dòng)弦線產(chǎn)生駐波后,采用間接方法測(cè)量相關(guān)各參量,再通過(guò)公式計(jì)算得到其固有頻率.本文采用計(jì)算機(jī)實(shí)測(cè)技術(shù)可直接對(duì)音叉的固有頻率進(jìn)行實(shí)時(shí)測(cè)量.通過(guò)實(shí)驗(yàn)可以看出計(jì)算機(jī)實(shí)測(cè)技術(shù)使得測(cè)量更為直觀、簡(jiǎn)單,數(shù)據(jù)采集處理更加科學(xué)、方便,不僅提高了實(shí)驗(yàn)的準(zhǔn)確度,同時(shí)也增加了實(shí)驗(yàn)的趣味性和技術(shù)性.
1 原實(shí)驗(yàn)方法
教材采用方法的實(shí)驗(yàn)裝置如圖1所示,音叉帶動(dòng)弦線振動(dòng)起來(lái)并形成穩(wěn)定的駐波后,測(cè)量相關(guān)參量,代入音叉固有頻率的測(cè)量公式計(jì)算得到音叉振動(dòng)的固有頻率.該方法中所使用的音叉固有頻率測(cè)量公式為

式中f為弦線的振動(dòng)頻率;M g為弦線繞滑輪端所掛砝碼的重力,即弦線的張力;n為弦線在張力M g下,調(diào)整弦線長(zhǎng)度后所出現(xiàn)的穩(wěn)定明顯駐波的半波數(shù),實(shí)驗(yàn)中可直接數(shù)出;L為弦線長(zhǎng)度,即弦線的振動(dòng)長(zhǎng)度;μ為弦線的線密度.

圖1 實(shí)驗(yàn)裝置圖
實(shí)驗(yàn)中,我們選用標(biāo)準(zhǔn)值為101.6 Hz的音叉進(jìn)行頻率測(cè)量.測(cè)量過(guò)程中,選取分度值為1 mm(儀器誤差為0.5 mm)的卷尺和分度值為20 mg(儀器誤差為10 mg)的物理天平,分別測(cè)得:弦線總長(zhǎng)度l=4.06 m,弦線的質(zhì)量 m=2.54 g,從而計(jì)算得到弦線密度μ=0.625 g/m,拉伸弦線砝碼質(zhì)量M=140 g,弦線的振動(dòng)長(zhǎng)度L=1.26 m,在該條件下弦線上顯示的穩(wěn)定駐波的半波數(shù) n=6.代入式(1)后計(jì)算得到:f=111.6 Hz.
根據(jù)間接測(cè)量量的不確定度傳遞公式,

在分析中引入的測(cè)量不確定度來(lái)源有:弦線振動(dòng)長(zhǎng)度L、弦線密度μ以及拉伸砝碼重力M g,其中,線密度μ的測(cè)量的不確定度源自弦線總長(zhǎng)度l和弦線質(zhì)量m的測(cè)量.
根據(jù)單次測(cè)量不確定度的定義,B類不確定度[1]由測(cè)量不確定度μB1和儀器不確定度μB2合成即測(cè)量不確定度μB1是由估讀引起,實(shí)驗(yàn)中其值取儀器分度值的1/2,儀器不確定度μB2一般可用均勻分布處理,即μB2=儀器誤差/故實(shí)驗(yàn)中各測(cè)量量的相對(duì)不確定度為:
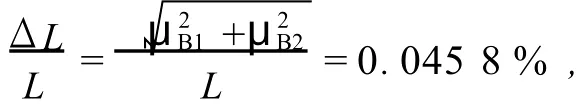

代入式(2),得到該方法測(cè)量音叉固有頻率 f的相對(duì)不確定度為Δf/f=0.232%.
2 計(jì)算機(jī)實(shí)測(cè)方法
采用計(jì)算機(jī)實(shí)測(cè)方法是在原實(shí)驗(yàn)裝置中加入儀器誤差為0.000 1 s的光電門傳感儀器、計(jì)算機(jī)接口,計(jì)算機(jī)及其相關(guān)數(shù)據(jù)采集與處理軟件.實(shí)驗(yàn)通過(guò)音叉帶動(dòng)弦線振動(dòng)形成穩(wěn)定的駐波,待弦線振動(dòng)穩(wěn)定后,在其某一波腹的平衡位置處安裝光電門傳感器(見(jiàn)圖2),對(duì)弦線振動(dòng)情況進(jìn)行實(shí)時(shí)數(shù)據(jù)采集,通過(guò)計(jì)算機(jī)接口將所采集到的弦線振動(dòng)信號(hào)直接傳入相關(guān)處理軟件中,可直接得到弦線的振動(dòng)頻率,即音叉的固有頻率.

圖2 實(shí)驗(yàn)裝置改進(jìn)圖
計(jì)算機(jī)實(shí)時(shí)測(cè)量采集的主要數(shù)據(jù)為實(shí)測(cè)時(shí)間和擋光時(shí)間.實(shí)測(cè)時(shí)間是指啟動(dòng)傳感器開(kāi)始測(cè)量到停止傳感器結(jié)束測(cè)量的實(shí)測(cè)時(shí)間段,如圖3中所例舉的 2個(gè)實(shí)測(cè)時(shí)間點(diǎn)(簡(jiǎn)稱實(shí)測(cè)點(diǎn)):0.365 7 s和0.424 7 s,這2個(gè)實(shí)測(cè)點(diǎn)所包含的時(shí)間段,即為所截取的實(shí)測(cè)時(shí)間段.擋光時(shí)間是指具有一定寬度的弦線掃過(guò)光電門時(shí)擋住光線的時(shí)間.當(dāng)弦線振動(dòng)穩(wěn)定后,弦線每掃過(guò)光電門1次,就會(huì)得到1個(gè)該實(shí)測(cè)點(diǎn)處的擋光時(shí)間值,如圖3實(shí)測(cè)點(diǎn)0.365 7 s處,測(cè)得的擋光時(shí)間為2.000 0×10-4s.波腹位置處的弦線在穩(wěn)定振動(dòng)的1個(gè)周期里都會(huì)有3次掃過(guò)平衡位置,故光電門每測(cè)得3個(gè)實(shí)測(cè)點(diǎn)就構(gòu)成1個(gè)振動(dòng)周期,周期值的大小即3個(gè)實(shí)測(cè)點(diǎn)所包含的實(shí)測(cè)時(shí)間段,這樣就直接測(cè)得了弦線振動(dòng)的周期,進(jìn)而也就得到了音叉振動(dòng)的頻率.

圖3 弦線振動(dòng)穩(wěn)定實(shí)時(shí)數(shù)據(jù)采集圖
選取了圖3中實(shí)測(cè)點(diǎn)0.365 7 s到實(shí)測(cè)點(diǎn)0.424 7 s之間的實(shí)測(cè)數(shù)據(jù),整理成弦線穩(wěn)定振動(dòng)實(shí)測(cè)時(shí)間點(diǎn)見(jiàn)表1.

表1 弦線穩(wěn)定振動(dòng)實(shí)測(cè)時(shí)間點(diǎn)列表

表2 周期計(jì)算列表
采用計(jì)算機(jī)實(shí)測(cè)方法對(duì)音叉固有頻率進(jìn)行測(cè)量,方法簡(jiǎn)單直觀,結(jié)果準(zhǔn)確度較高,但是實(shí)驗(yàn)中對(duì)于測(cè)量條件的要求較高:
1)光電門安裝的位置不僅要安裝在弦線振動(dòng)形成駐波后的波腹處,還要調(diào)節(jié)到波腹的平衡位置處.這是因?yàn)橄揖€形成駐波后的振動(dòng),波腹處的振幅最大,波腹的平衡位置處,振動(dòng)速度最大,這樣確保了是在弦線振動(dòng)的最明顯處進(jìn)行數(shù)據(jù)測(cè)量,測(cè)量結(jié)果也就相對(duì)準(zhǔn)確.
2)一定要在弦線穩(wěn)定振動(dòng)后才可進(jìn)行振動(dòng)頻率的實(shí)時(shí)測(cè)量.弦線是否為穩(wěn)定振動(dòng),首先判斷弦線振動(dòng)是否形成駐波,而不是處于弦線的任意振動(dòng)狀態(tài);再判斷其通過(guò)光電門的擋光時(shí)間值是否穩(wěn)定不變.當(dāng)某個(gè)實(shí)測(cè)時(shí)間段內(nèi),擋光時(shí)間值穩(wěn)定不變,則表明這個(gè)實(shí)測(cè)時(shí)間段內(nèi)弦線振動(dòng)已達(dá)到實(shí)驗(yàn)要求的穩(wěn)定程度.從圖3中可以看出,在0.365 7 s到0.424 7 s這段時(shí)間內(nèi),實(shí)測(cè)點(diǎn)的擋光時(shí)間均為2.000 0 s,表明該段時(shí)間內(nèi)弦線振動(dòng)的穩(wěn)定性已滿足實(shí)驗(yàn)要求.
3 兩種方法的比較
比較測(cè)量音叉固有頻率的兩種方法,可知兩種方法都需要穩(wěn)定的駐波作為實(shí)驗(yàn)條件,但兩種方法分別采用了不同的測(cè)量方式,因而測(cè)量結(jié)果有著很大的差別.

表3 音叉固有頻率兩種測(cè)量方法比較
從表3的數(shù)據(jù)中可以看出:原實(shí)驗(yàn)方法需測(cè)量的物理量比實(shí)測(cè)方法要多,因此引入的測(cè)量量的相對(duì)不確定度多且計(jì)算繁雜;從2種方法的測(cè)量結(jié)果的相對(duì)不確定度,可以看出原實(shí)驗(yàn)方法的測(cè)量結(jié)果不確定度小于計(jì)算機(jī)實(shí)測(cè)方法,即原方法的測(cè)量精密度較高;從2種方法得到的測(cè)量值與標(biāo)準(zhǔn)值101.6 Hz的比較可以看出,采用實(shí)測(cè)方法測(cè)量的結(jié)果更接近真值.
4 結(jié)束語(yǔ)
通過(guò)計(jì)算機(jī)實(shí)測(cè)精確測(cè)量音叉的固有頻率,并與教材使用的實(shí)驗(yàn)方法和計(jì)算出的結(jié)果進(jìn)行對(duì)比,充分體現(xiàn)了計(jì)算機(jī)實(shí)測(cè)的應(yīng)用既簡(jiǎn)化了實(shí)驗(yàn)測(cè)量步驟,也提高了測(cè)量結(jié)果的準(zhǔn)確度和實(shí)驗(yàn)效率.計(jì)算機(jī)實(shí)測(cè)技術(shù)在大學(xué)物理實(shí)驗(yàn)中的應(yīng)用,不僅帶來(lái)了實(shí)驗(yàn)技術(shù)與測(cè)量手段上的革新,也激發(fā)了學(xué)生做實(shí)驗(yàn)的熱情與興趣.
[1]沈元華,陸申龍.基礎(chǔ)物理實(shí)驗(yàn)[M].北京:高等教育出版社,2003:8-15.
[2]李學(xué)金.大學(xué)物理實(shí)驗(yàn)教程[M].長(zhǎng)沙:湖南大學(xué)出版社,2006:141-146.
[3]周麗,蔣亞玲.用計(jì)算機(jī)研究音叉共振頻率和雙臂質(zhì)量的關(guān)系[J].大學(xué)物理實(shí)驗(yàn),2007,20(3):78-81.
[4]陳瑩梅,陸申龍.音叉的共振頻率與雙臂質(zhì)量的關(guān)系研究及其應(yīng)用[J].物理實(shí)驗(yàn),2006,26(7):6-9.
[5]漆安慎,杜嬋英.力學(xué)[M].北京:高等教育出版社,2005:355-365.
[6]彭菊村,孫春峰.普通物理實(shí)驗(yàn)[M].武漢:湖北科學(xué)技術(shù)出版社,2005:42-43.
[7]姚久民,田廣志,祝玉華.用頻譜分析法研究弦振動(dòng)實(shí)驗(yàn)[J].物理實(shí)驗(yàn),2009,29(12):31-33.
[8]周勇,李更磊,鄭小平.對(duì)光電門測(cè)得的瞬時(shí)速度的誤差分析[J].物理實(shí)驗(yàn),2009,29(1):24-26.
[責(zé)任編輯:郭 偉]
Measuring natural frequency of tuning fork by computer
L IDing-mei,GAN Yi-wen,FENG Ling
(College of Physics Science and Technology,Shenzhen University,Shenzhen 518000,China)
The natural frequency of tuning fork ismeasured in real-time by computer.Compared w ith the originalmethod,this imp roved measurement by computer iseasier and more intuitive,the result ismore accurate.
tuning fo rk;natural frequency;real-time testing
O421.2;O4-39
A
1005-4642(2010)11-0044-03
2010-02-28;修改日期:2010-05-18
李定梅(1988-),女,重慶人,深圳大學(xué)物理科學(xué)與技術(shù)學(xué)院應(yīng)用物理專業(yè)2007級(jí)本科生.
封 玲(1972-),女,江蘇南京人,深圳大學(xué)物理科學(xué)與技術(shù)學(xué)院副教授,主要從事大學(xué)物理實(shí)驗(yàn)教學(xué)的數(shù)字化、信息化研究.

