鉆井井架可靠度分析

陳 科 孫 偉 劉春陽 官振樂

勝利油田 技術檢測中心設備站 （山東 東營 257000）

鉆井井架可靠度分析

陳 科 孫 偉 劉春陽 官振樂

勝利油田 技術檢測中心設備站 （山東 東營 257000）

井架作為石油鉆井生產的一種特種設備，價格昂貴，安全性要求高，井架可靠性分析和評估顯得尤為重要。基于可靠性理論，根據井架模型的實測數據，給出了井架可靠性指標的判斷方法。最后給出了井架模型失效概率的計算方法和計算結果。

井架 失效概率 可靠度

井架作為鉆機系統設備中的關鍵部分，其安全性能直接關系到整套鉆機系統的安全生產，現已被納入評價鉆機體系安全運行的項目之中。在長期生產使用過程中，由于拆裝、運輸、超載和腐蝕等各種因素的影響，井架各桿件、桿件間連接及整體都會出現不同程度的損傷缺陷，這些損傷缺陷使井架的承載能力低于原設計，導致安全載荷的未知，造成生產安全隱患。為確保鉆機鉆井過程的安全運行，準確評定鉆機井架承載能力意義重大。井架作為石油鉆井生產的一種特種設備，價格昂貴，安全性要求高。在一般使用條件下，井架總服役期超過10年者，應予以報廢。調查表明：許多油田鉆井井架使用期已超過10年，但根據油田目前的經濟狀況，立即更換新的似乎又不可能，因此開展井架可靠性鑒定就顯得尤為重要。

井架結構可靠度

在用井架可靠度鑒定要解決的根本問題是：井架使用多年之后，在井架有缺陷、損傷情況下，保證井架能滿足鉆井作業的各種要求。一般而言，在用井架應滿足下列各項要求[1]：

（1）能承受正常鉆井作業中可能出現的各種荷載作用。

（2）正常鉆井時，井架及其各構件具有良好的工作性能。

（3）在正常使用維護下，井架具有足夠的耐久性。

井架在規定時間和規定條件下完成規定功能的概率用pR表示，而井架結構不能完成規定功能的概率稱為失效概率以pf表示，pR+pf=1，pR和pf都能用來度量結構的可靠性，但習慣上選用pf度量。pf大，可靠性低；pf小，可靠性高。

井架可靠度通常受荷載種類、材料強度、幾何尺寸等隨機因素及計算公式不確定性等的影響。通常將這些隨機因素稱為基本變量，用xi(i=1,2…,n)表示，井架由其極限狀態來設計，可建立包括各有關基本變量的關系式：

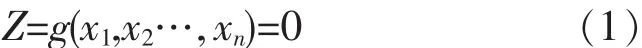
式（1）稱為極限狀態方程，其中Z=g(x1,x2…,xn)稱為井架的功能函數。當采用井架抗力R和荷載效應S為綜合基本變量時，則結構功能函數可表示為：

當Z＞0時，結構處于可靠狀態；

當Z＜0時，結構處于失效狀態；

當Z=0時，結構處于極限狀態。

井架的可靠性指標與失效概率的關系[2-4]

設結構抗力R、荷載效應S為互相獨立的基本變量,且若R、S均為正態分布則Z為正態分布。其均值和標準差分別為uR，uS，uZ和σR，σS，σZ，表達式為：

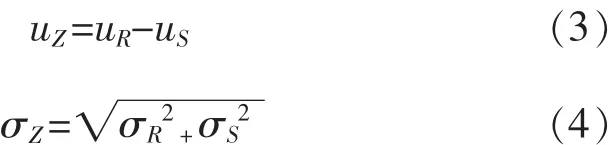
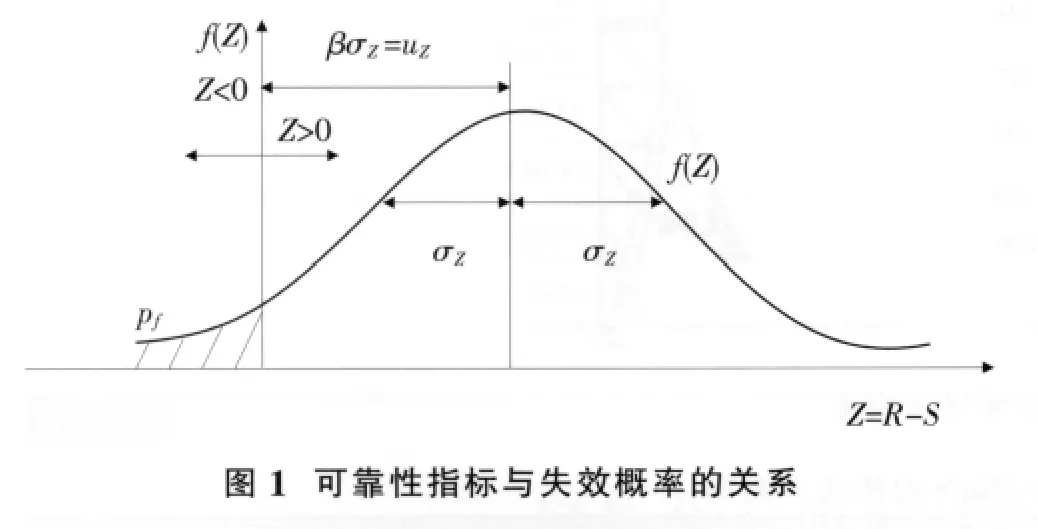
由圖1所示，功能函數Z=R-S為正態分布，f(Z)為功能函數Z的概率密度函數，其中陰影部分的面積Z＜0，概率即失效概率pf：

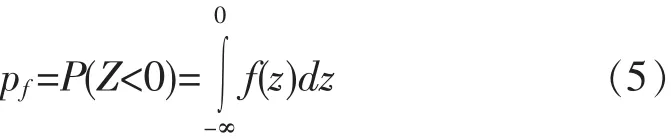
設βσZ=uZ

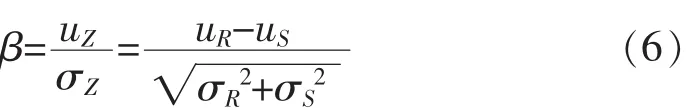
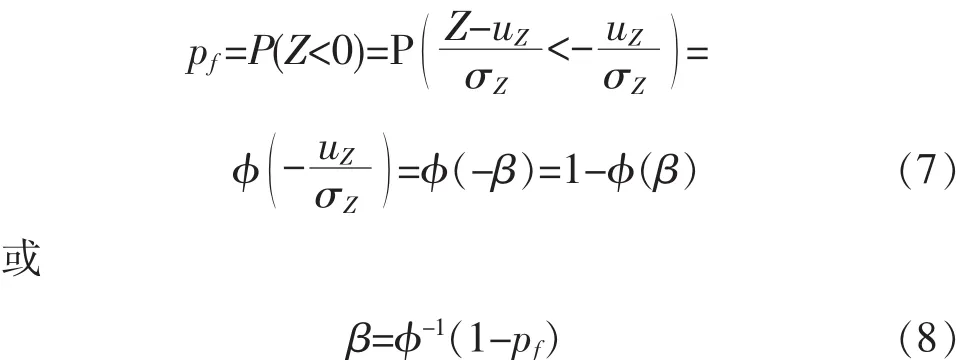
式中φ為標準正態分布函數。 β與pf存在著一一對應關系。β增大，pf減少;β減少，pf增大。β也具有與pf相對應的物理關系，β的大小表示可靠度的大小，β越大時結構越可靠。β稱為結構的可靠指標。

井架結構整體可靠度

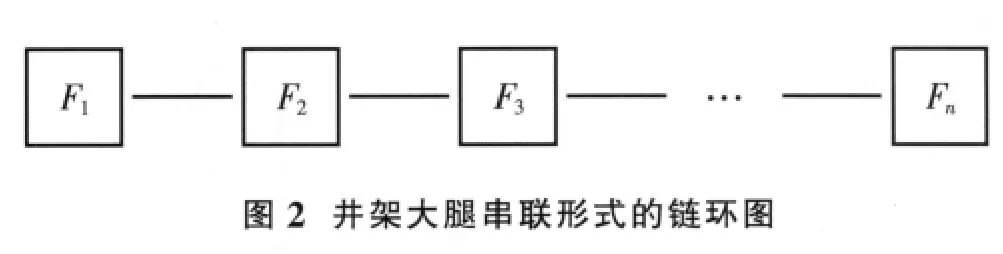
井架結構是由許多構件組成的多次超靜定結構，一個截面、一根構件的局部破壞并不一定標志整個井架的破壞，從系統角度來講，實際井架是由若干個串聯系統和并聯系統組成的混聯系統。理論上，分析這種混聯系統的可靠度時，可先計算各子系統(串聯或并聯系統)的可靠度，然后將各子系統視為一個構件，再分析整個結構的可靠度，精確計算是相當繁瑣的。井架的工作荷載一般為大鉤鉤載(豎直向下)，井架大腿上任一個斷面失效，將使得井架整體結構失效，因此，井架整體可靠性分析可采用井架大腿立柱構件以串聯形式的鏈環模型來描述，較好地反映了實際，如圖2所示。

井架結構模型可靠度的計算

1 井架模型構件抗力、荷載效應的統計分析

井架模型構件抗力指的是構件抵抗破壞或變形的能力[5]，在進行評定時，根據公式：

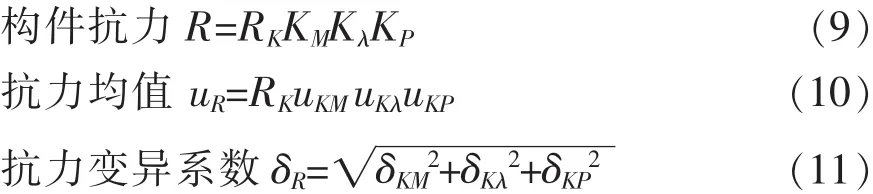
式中，RK為按規范計算的構件抗力 (即強度的標準值)；Kλ為構件幾何參數的不定性；KM為材料強度或剛度的不定性；KP為構件計算模式的不定性。

表1列出了井架模型在試驗時的實測結果，它初步反映出試件長度及受力偏心等多種不定(隨機)因素的影響。由于計算的目的是確定模型的壓潰載荷，而破壞準則是井架模型的整體失穩壓潰，并不是模型某桿件局部發生屈服變形，因此材料抗力應按井架模型的柔度λ=77.72取井架模型材料的臨界應力R=227.26MPa，而不是取材料的屈服極限。經大量的統計分析可知,井架各截面應力，服從正態分布[6]。

2 井架模型失效概率的計算

表1 井架模型材料在壓縮試驗時的臨界壓力

如圖3所示，井架由左、右大腿連接而成，而左、右大腿均由4段格構式組成，任一根大腿的失效都將引起整個井架的失效，這樣整個井架都可看作是兩個串聯子系統，每根大腿20個單元桁格為串聯模式，所以每根大腿應取20個單元桁格結構中各截面失效概率之和，兩大腿失效概率最大值代表了整個井架的失效概率。截面編號見圖3，表2和表3分別給出了井架模型在鉤載20、28kN時的失效概率計算值。

結論

表2是井架模型在鉤載在22kN時，計算得到的失效概率pf為25.45%，pR=74.55%，由于pR＞pf，井架結構處于安全狀態。表3是井架模型在鉤載28kN時，計算得到的失效概率pf為53.26%，pR=46.74%，pR＜pf，井架處于不安全狀態。

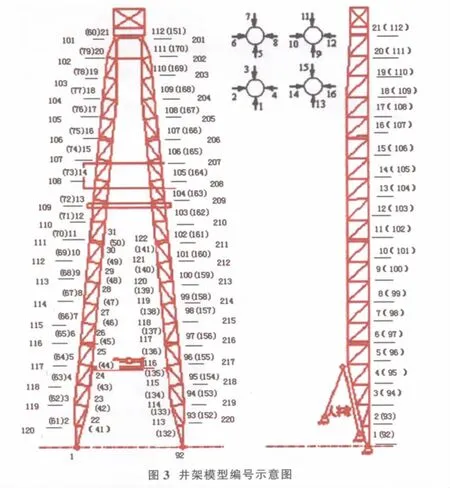
表2 井架模型在鉤載20kN時的失效概率

由井架模型最大荷載試驗可知，雖然大鉤荷載實際已加到22kN，但由于這時井架模型的可靠概率大于失效概率，因此井架模型不會發生破壞。由此可見，用可靠性方法分析井架模型的可靠度是可行的。本文基于可靠性理論，利用井架模型的實測數據，給出了井架模型失效概率的計算方法和計算結果，為進行井架結構定量的可靠性分析提供一種合理方法。

表3 井架模型在鉤載28kN時的失效概率

[1]常玉連,劉玉泉.鉆井井架、底座的設計計算[M].北京：石油工業出版社,1994.

[2]Rao S S.The Finite E1ement M ethod in Engineering[M].Oxford：Pregramon Press，1982.

[3]Chajes A.Principles of Structural Stability Theory[M].New Jersey：Prentice-Hall，Inc.Englewood Cliffs，1974.

[4]Chen Y Z，Chung Y E.Buckling Loads of Columns with Varying Cross Sections[J].The Journal of Engineering Mechanics，1989，115 (3).

[5]張汝清，殷學綱，董明.計算結構動力學[M].重慶：重慶大學出版社，1987.

[6]Timoshenko S P，Gere J M.Theory of Elastic Stability[M].NewYork：M cgraw-Hill，Inc，1961.

The drilling derrick,as one special device of petroleum drilling production,is very expensive and is highly required in security,so it seems to be very important to do an analysis and evaluation on the reliability of drilling derricks.Based on the theory of reliability and measured data of derrick models,the methods of judging the reliability index of drilling masts are offered in the paper, coupled with the calculating methods and the calculated result about the failure probability of drilling derrik models.

drilling mast/derrick;failure probability;reliability

陳科（1978－），男，現從事設備檢測評估工作。

黃永場

2010-05-17