最大輸沙率法推求石馬河穩定河寬

楊勝發，袁觀棟，羅羚源，胡鵬飛

(重慶交通大學河海學院，重慶400074)

航道整治工程中經常遇到確定整治河段岸線問題，即穩定河寬問題。通常運用最大法輸沙率和穩定河槽寬度法，筆者采用最大法輸沙率推求穩定河寬。通過穩定河寬的確定為河道的整治提供最優方案。

石馬河位于重慶市奉節縣草堂鎮，距長江入匯口(白帝城附近)6.5 km，屬于大比降卵石河流，在洪水期流量、流速和比降均較大，并且有部分彎曲河段。石馬河河道治理工程是草堂鎮場鎮規劃及工業園區建設的重要組成部分，若堤防的防護措施考慮不當，將很容易造成其水毀，保持工程河段穩定的河床寬度是保證河段穩定的關鍵。

1 石馬河河段基本特征

石馬河為三峽庫區長江北岸的一條支流，屬典型的山區河流。工程河段尾部以上控制流域面積184 km2，河道全長 19.2 km，河道平均比降 31.4‰。工程段50 a一遇流量為1 170m3/s，暴雨時期洪水具有漲水快(5h左右)，持續時間短(2～3h時左右)，退水時間長(15h以上)的特點。

石馬河為典型的大比降卵礫石河流，河岸局部有基巖控制，河床組成主要為卵礫石和漂石。在最近20多年內，未出現大的暴雨洪水，河床變化不明顯。

2 河床寬度與輸沙率3種觀點

在已知流量、河床組成、河道比降情況下，河道輸沙率與河寬的關系目前有3種觀點:①輸沙量隨著寬度的減少而增加(Henderson［1］);②輸沙量隨著寬度的增加而增加(Bagnold［2］，Parker［3］);③前 2種形式都存在，在某個特殊的寬度輸沙率有一個最大值(Gilbert［4］)。通過分析目前的 3種觀點，都存在一定的缺陷。

Henderson假設單寬推移質輸沙量qs與單寬流量q是簡單的指數關系，即:

斷面總輸沙量為Qs與流量的關系Q:

式中:B為河槽寬度。

當k＞1時，輸沙量隨寬度的減小而增加。Henderson根據 Einstein［5］推移質輸沙率公式，認為k=2。

Henderson方法中Einstein公式不是簡單的指數公式，在不同水流強度時k值不一樣。直接令k=2，通過式(1)推斷輸沙量隨寬度變化的趨勢得到的結果不可靠。

Parker針對卵礫石河流，推導了斷面輸沙量與寬度的關系。在水流條件與起動拖曳力相比相差不大時，單寬輸沙量、單寬流量與水深有如下關系:

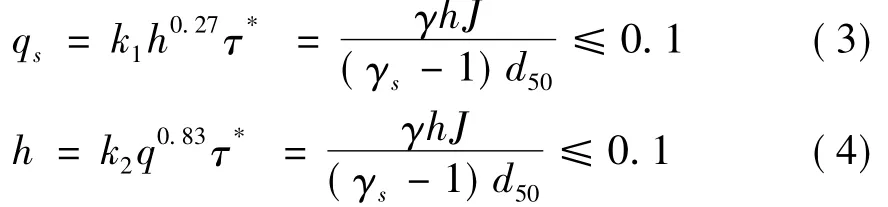
通過式(3)和式(4)可以得到:

Parker主要限制條件是水流條件強度不大，泥沙運動強度較弱，床面阻力主要是定床阻力，可得到式(3)和式(4)。對于水流條件強度較大，泥沙運動強度較強，床面有沙波運動，得出的關系與式(3)和式(4)有所出入。對于卵礫石河流來說，式(5)不能代表所有水流強度情況下的輸沙量方程。

Michael［6］根據輸沙率公式的特征，斷面輸沙量表達成如下形式:

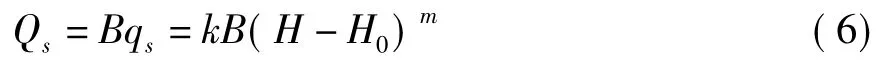
對式(6)求導，

根據謝才－曼寧公式:

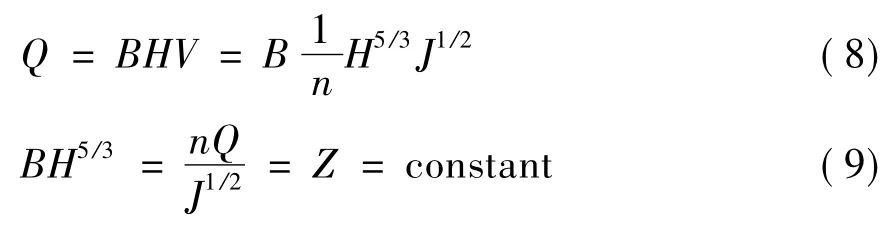
對式(9)求導，

將式(10)代入式(7):

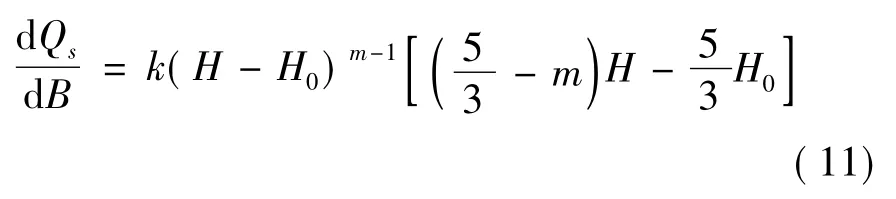
將式(12)代入式(6)可得到最大輸沙率對應的寬度。

Michael［6］在最大輸沙率對應的寬度的分析中有以下問題未加以考慮:

1)未劃分河床阻力河岸阻力。在相同流量下，河床寬度較小時，水深較大，河岸阻力較大。如不考慮河岸阻力得到的剪切力偏大;

2)河床輸沙強度不同，其糙率(阻力)不是常數，應考慮動床阻力。

3 本文方法推求最大輸沙率的寬度

在流量一定的情況下，最大輸沙率對應的寬度可能的3種情況皆因選擇的輸沙率公式和假設條件不同而得到的。對于大比降卵礫石河流，主要是河道的水力計算和輸沙率公式的選擇。

3.1 河道水力計算

已知流量Q、河床比降J和河床組成，假設水深為H，形狀為矩形，河岸糙率nw。

1)計算Rb

由謝才－曼寧公式計算出河床的綜合糙率n:

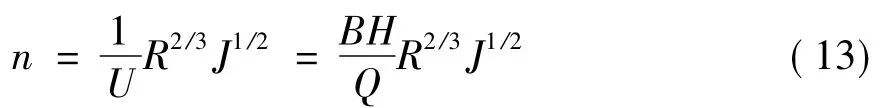
根據Einstein將綜合阻力劃分為河岸阻力和河床阻力的方法，計算出nb和Rb:

2)計算沙粒阻力(R'b)

Einstein and Barbarossa推薦對數流速公式計算R'b:

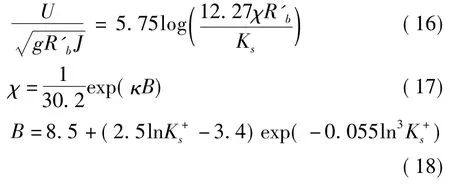
3)沙波阻力(R″b)

采用楊勝發［7］等研究明渠動床的沙波阻力方法，當相對光滑度h/d65＜150時，沙波阻力與h/d65有關，經回歸分析提出了計算沙波阻力的公式:

低能態:高能態:

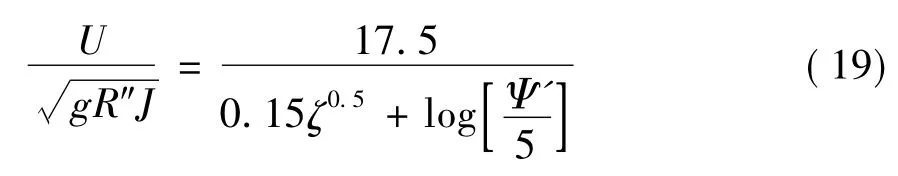
按照上式可計算出R″b。

4)判斷Rb(第1步計算)是否等于(第2、3步計算)，如不相等，重新假設H，重復1)～4)步。

3.2 床面有效切應力計算

流量一定，隨著河床寬度B減小，水深H增加，寬深比B/H減小。寬深比B/H小到一定程度時，河床阻力受到邊壁的影響。Cao［8］分析了寬深比對床面有效切應力的影響:

3 .3 輸沙率計算

筆者選取 Ackres 和 White［9］，Einstein 修正式［10］，Meyer－Peter公式［5］進行計算和分析。

水流強度:

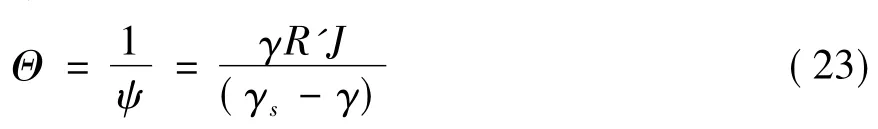
輸沙強度:

Ackres和 White 式［9］:Einstein 修正式［10］:

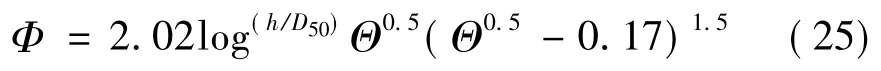
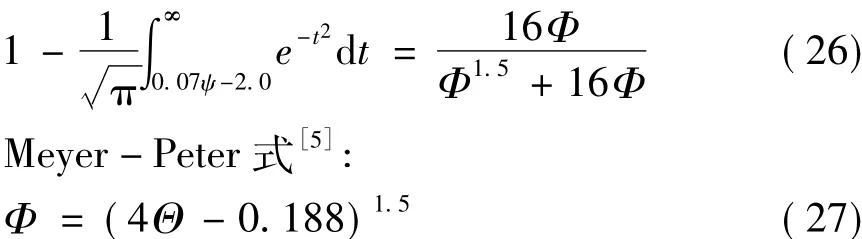
4 石馬河最大輸沙率的寬度計算結果與分析

石馬河河道治理工程的標準使用年限為50 a，防洪標準為50 a一遇洪水，因此研究石馬河來流的洪水控制流量為50 a一遇洪水(Q50=1 170m3/s)。石馬河控制流量、比降、河床級配組成以及邊壁糙率作為不同寬度輸沙率計算的初始條件見表1。按照本文的計算方法，計算出石馬河不同寬度的輸沙量見表2。

表1 石馬河輸沙率計算初始條件Tab.1 Initial conditions of sediment transportrate ratecalculation of the Shima River

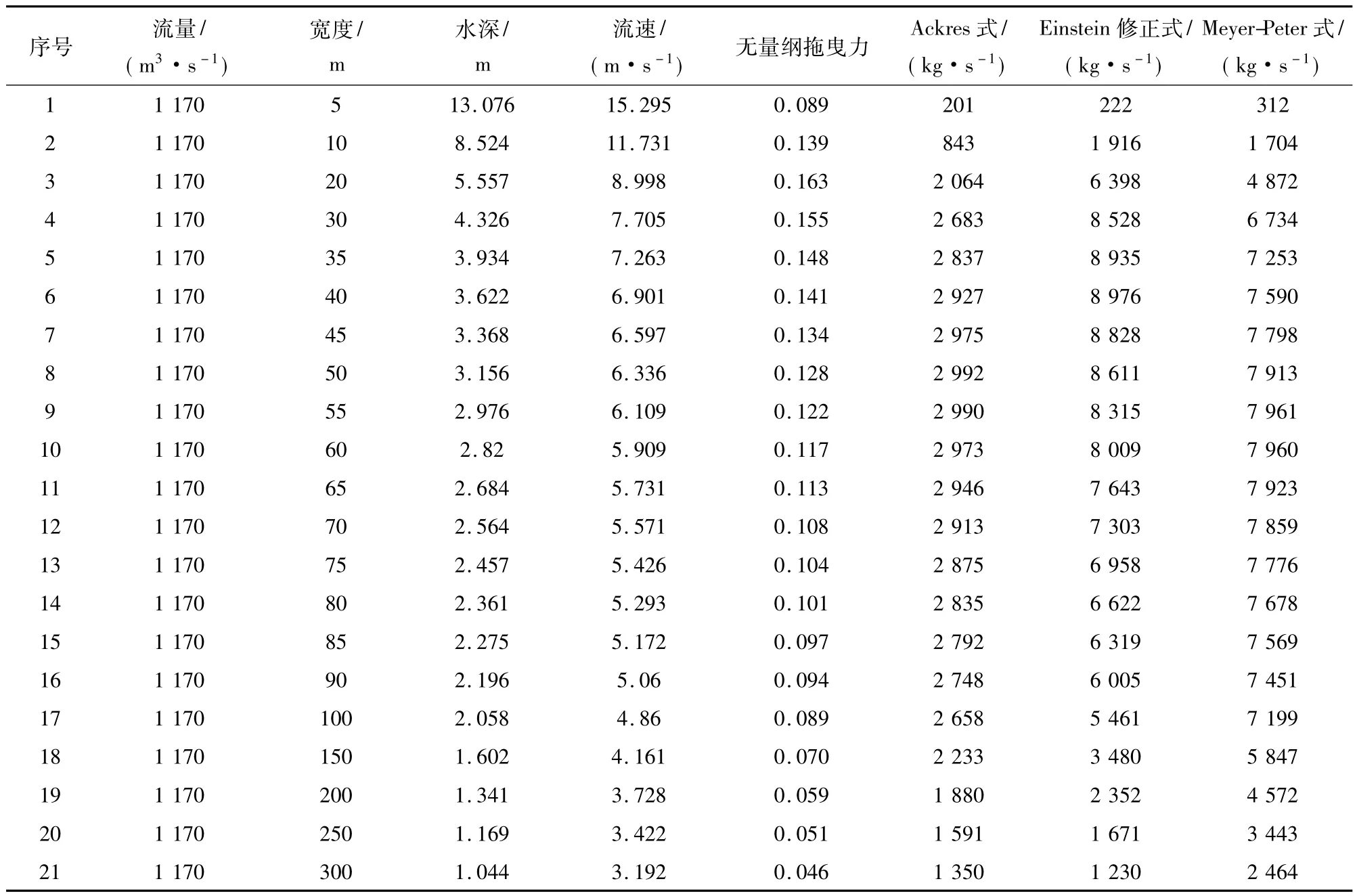
表2 石馬河不同寬度的輸沙率Tab.2 Sediment transport rate of different width of the Shima River

為了使計算結果更直觀，將表格數據圖表化，對比3種輸沙強度公式下輸沙率與寬度的關系，以及各公式輸沙率比率與寬度關系，詳情如圖1～圖2。

圖1 各公式輸沙率與寬度的關系Fig.1 Relation between caculation sediment transport rateand width according to different formula

圖2 各公式輸沙率比率與寬度的關系Fig.2 Relation between sediment transport rate and width according to different formula

計算結果顯示，采用不同的輸沙率公式，皆可得到相同的規律:在流量一定的情況下，在寬度較小時，輸沙率隨著寬度的增加而增減，當達到某一寬度時，輸沙率最大，最后隨著寬度的增加，斷面輸沙率減小。

總的來看，在寬度為40～70m，各公式計算的輸沙率是最大輸沙率的96%以上。在寬度為40～70m時，水深為 2.56～3.62m;斷面平均流速為5.5 ～6.9m/s;無量綱拖曳力為 0.10 ～0.14。采用不同的輸沙率公式，最大輸沙率對應的寬度有所變化，Ackres、Einstein修正式和 Meyer－Peter公式計算的最大輸沙率對應的寬度分別為45，40和60m。按照最大輸沙率對應的石馬河河槽寬度為40～70m。

5 物理模型實驗結果

物理模型布置了30，40，60，80m共4種河寬，在保持來流條件一致的情況下，分析了河段內沖刷深度與寬度、河道水深、流速以及河段沖淤情況等等，重點分析了輸沙量和河道最大沖淤高度與面積。

總結物模實驗結果，30m河寬整體沖淤較平衡，局部沖刷較大;40m河寬沖刷尺度與30m相差不大，但水深較小，整體沖刷量小;60m整體都處于弱于狀態;80m沖刷尺度很大。綜合分析實驗結果提出40m+60m方案，采用整治河段進口為60m河寬，下游為40m河寬，整體沖淤較理想。

6 結語

在對石馬河工程河段基本資料分析的基礎上，對比目前輸沙率與穩定河寬的幾種觀點，提出最大輸沙率的穩定河寬方法，利用數學推導法推求河道的水力計算和輸沙率公式，結合物理模型實驗進行驗證計算得出輸沙率與河道寬度的基本規律:在流量、河床比降、河床組成一定的情況下，開始階段輸沙率隨寬度的增加而增加，當寬度達到一個最大值后，隨寬度進一步增大，輸沙率反而減小。分析大量計算結果，將其量化為直觀的圖標形式，最終確定最大輸沙率對應的石馬河河槽寬度為40～70m。

物理模型實驗采用4種不同的河寬，在來流條件一致的情況下，測量了沖淤尺度、水深、流速等參數，重點分析整治河段沖淤情況，最終得出40m+60m的實驗方案。

數學推導結果和物模實驗結果基本一致，故利用最大輸沙率法推求穩定河寬的研究成果可應用于指導石馬河河道治理工程。

［1］Henderson F M.Open channel flow［M］.New York:MacMillan Publishing Co.，1996.

［2］Bagnold R A.Bedload transport by natural river［J］.Water Resour，1979，13(2):303 －312.

［3］Parker G.Hydraulic geometryof active gravel river［J］.Hydr Div，1979，105(9):1185－1201.

［4］Gilbert G K.The transportation of debris by running water［M］.Washington，D.C.:U S Government Printing Office，1994.

［5］錢寧，萬兆惠.泥沙運動力學［M］.北京:科學出版社，2003.

［6］Michacel A C，George A G.Influence of channel width on bed load transport capacity［J］.Hydr Div，1988，113(12):1489 －1509.

［7］楊勝發，周華君，胡江.內流河寬淺變遷河段水沙運動規律研究［M］.重慶:重慶大學出版社，2007.

［8］Cao S，Knight D.Design for hydraulic geometry of alluvial channels［J］.Journal of Hydraulic Engineering，1998，124(5):484－492.

［9］Ackers P，White R.Sediment transport-new apporach and analysis［J］.Journal of the Hydraulics Division，1973，99(11):2041 －2060.

［10］王興奎.河流動力學［M］.北京:科學出版社，2007.