分形特征的模擬電路故障診斷方法

李 偉，李天偉，王桂軍，易成濤

（海軍大連艦艇學院航海系，遼寧 大連 116018）

1 引 言

據統計，在電子系統中模擬電路的故障占到總故障的80%。模擬電路故障診斷成功與否關鍵集中在信號測量、信號處理、信號特征提取及分析診斷幾個環節，由于元器件容差、功能和結構的復雜性、非線性及不確定性等因素，導致信號特征提取環節對故障診斷結果的判定產生較大影響。因此，尋求一種有效的故障診斷方法，對于確保設備處于良好工作狀態具有重要意義。

分形理論是非線性科學中的一個活躍的數學分支，其研究對象是自然界和非線性系統中出現的不光滑和不規則的幾何形體[1-2]，對應的定量參數是維數，在旋轉機械[3]和電力電子電路故障診斷[4]及電路噪聲分析[5]等故障診斷和電路相關領域都有了一定的應用和研究。電路中存在混沌現象是在理論和實踐中證明了的不爭的事實[6]。該文將其引入模擬電路信號分析領域，在探討電路信號分形特征的基礎上，利用它進行了電路故障的診斷，取得了良好的效果。

2 信號預處理與分形特征提取

電路運行狀態與其各種故障征兆之間存在著因果聯系，如電壓、電流、溫度、紅外等，模擬電路的每一種故障狀態就是一個樣本，同一類故障出現的情況可能千差萬別，但在特征上表現出共性，根據這些特征可以區別其他類型的故障。模擬電路中存在著不少非線性現象，在一定程度上可以用非整數的分形維數進行描述。如果電路偏離了正常的工作狀態時，決定該電路狀態的參數的吸引子就發生變化，相應的分形維數也要發生變化，即分形維數往往隨著電路狀態的改變而改變。因而可以把分形維數作為反映電路故障的特征量，通過電路分形維數的變化判斷電路是否偏離了正常狀態，是否出現了故障。

故障特征信息的提取，對于模擬電路故障診斷是非常重要的環節，分形和混沌是非線性領域的主要研究內容之一，它的發展對識別和預測復雜的非線性信號系統提供了新的方法論。分形理論用來刻畫對象的不規則性和自相似性，在處理復雜非線性系統中具有獨特的優點。運用分形理論，提取有用的診斷信息，不僅可以定性，而且可以定量地分析系統的工作狀態，從而實現對模擬電路的故障診斷，提高對故障的識別和診斷能力。

2.1 分形盒維數

容量維數的定義，提出了一種測量分形的方法。取邊長為ε的小盒子，把分形集覆蓋起來。由于分形集內部有各種層次的空洞和縫隙，有些小盒子會是空的。計算有多少盒子不是空的，把這個數目記為N（ε）。然后縮小盒子的尺寸ε，計算得到的N（ε）自然要增大。根據前面的定義，只要在雙對數坐標紙上畫出logN（ε）對logε的曲線，其直線部分的斜率就是此分形集的盒子維數Db[7]，用式（1）表示為：

對于實際計算，只要分維小于二維或在二維附近，相空間維數也不高時，就是可行的。

2.2 模擬電路信號分形特征提取算法

根據盒維數的定義，網格越小計算結果越準確。分形維數受信號噪聲影響較大，因此在計算分形維數時應對原始數據進行降噪處理。對于非線性系統，由于信號的頻譜和噪聲的頻譜都表現為寬帶連續譜，產生的噪聲以傳統的線性濾波方法則效果不佳。奇異值分解降噪[8]是基于噪聲與系統信號對相空間軌道矩陣的奇異值的不同影響進行降噪的，能有效地去除非線性信號中含有的噪聲。

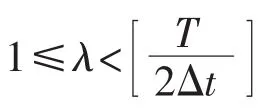
（1）相空間重構。用時延法重構相空間軌道矩陣：

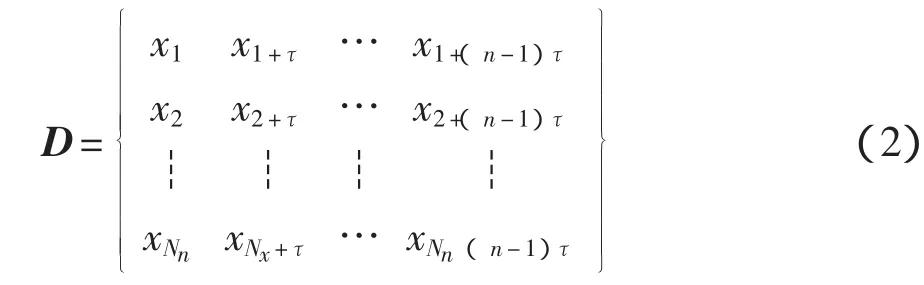
式中：τ——時間延遲；

n——嵌入維數；

n——重構相空間中向量的個數，Nn=N-（n-1）τ，Nn>>n。

（2）奇異值分解[6]。對軌道矩陣D進行奇異值分解（SVD）：

式中，S 是 DTD 的特征向量矩陣，∑=diag（λ1，λ2，…，λn），λ1，λ2，…，λn是矩陣D的奇異值，且有λ1≥λ2≥…λn≥0。噪聲將會使所有的奇異值都大于零，假設矩陣的秩為k，則前k個奇異值要遠大于其他奇異值。

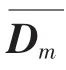
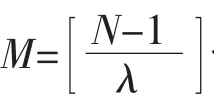
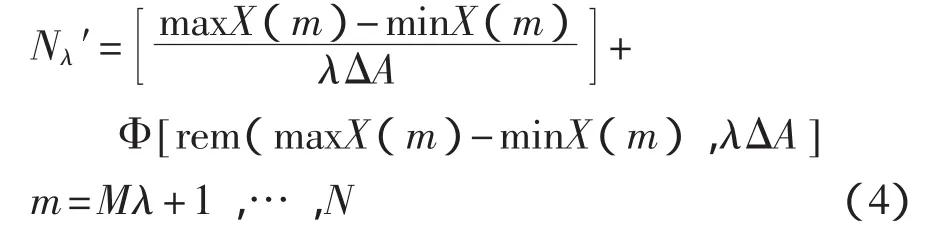
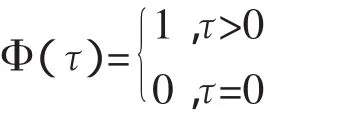
時間軸上的第 p（p=1，2，…，M）個等間隔區間內，與曲線相交的網格數Npλ為：

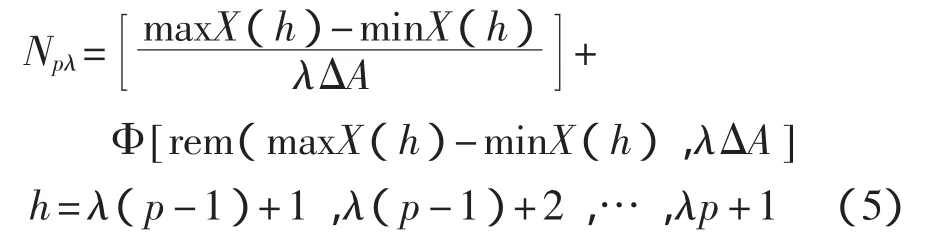
則在尺寸為λΔt×λΔA的矩陣網格下，與電路分形噪聲波形曲線相交的總網格數Nλ為：

（5）最小二乘法計算盒維數。在k的取值范圍內，去掉超過2和小于1的野點數據，改變λ值得到一系列 Nλ，再用最小二乘法對數據（Inλ，InNλ）進行線性方程回歸，斜率就是盒維數，就得到電路分形噪聲信號的盒維數。

3 以分形特征為輸入量的故障診斷方法

模擬電路故障診斷的研究經歷表明，利用單一信息、采用單一手段、基于單一理論的故障診斷方法是難以解決模擬電路故障診斷中的重重困難的，同樣，單獨一個測試節點所獲取電路信息的分形特征也很難全面的表征電路狀態。信息融合是將來自某一目標的多個傳感器或多源的信息進行綜合處理，從而得出更為準確、可靠的結論[9]，具有多信息量、多層次、多手段等優點，將其應用于模擬電路故障診斷，使診斷系統更為優越，可望解決以往諸方法中所普遍存在的由于診斷信息不足所帶來的電路可測性難題以及由于元件容差所帶來的問題。

3.1 分形維數隸屬度的計算

對于信號的不同狀態，以不同的采樣周期進行求解分形特征，對于采樣周期Δti，相應計算出的分形維數為dΔti，定義分形維數隸屬度函數為z（Δti，dΔti），以此來表征采樣周期Δti和分形維數dΔti之間的關系。以特定采樣周期所獲得的分形維數為中心維數點向兩側進行模糊化處理，按正態分布分配分形維數隸屬度：

通過測試被診斷電路的多節點輸出，求出每一節點在某故障條件下對應的分形維數隸屬度值，以此作為模擬電路故障的分形診斷方法模式識別的特征分量。

3.2 神經網絡信息融合步驟

電路運行狀態與各種故障征兆間存在因果聯系，但這種復雜關系很難直觀表述，而神經網絡可根據當前系統所接受的樣本的相似性，確定分類標準，同時可以采用特定的學習算法獲取知識，得到不確定性推理機制，非常適合信息融合技術的要求[10]。基于神經網絡信息融合技術的模擬電路故障診斷方法將人工神經網絡引入信息融合之中，屬于特征層融合，同時結合模糊集合論進行故障判斷。基于分形特征的模擬電路故障診斷原理框圖如圖1所示，按照故障診斷的要求以及測試分量的特點選取合適構建模擬電路故障診斷信息融合模型的BP網絡模型，進行模擬電路運行狀態診斷識別的診斷步驟為：

（1）依據獲取的測試信息采用合適的學習方法，對構建的神經網絡進行學習訓練，確定網絡的聯接權值和聯接結構，構建用于故障診斷的信息融合模型。

（2）所有節點的分形維數隸屬度值矢量作為神經網絡的輸入，網絡輸出為融合后該癥狀屬于各類故障的隸屬度值矢量。在此過程中，充分利用利用神經網絡的自學習和自組織功能，不斷調整自己的結構和權值，滿足測試條件不斷變化的實時要求，提高故障診斷的可靠性。

（3）利用基于規則的判定原則進行故障決策。

故障決策一般遵守3條規則：隸屬度函數值最大原則；隸屬度函數值閾值原則；最大最小隸屬度函數值之差閾值原則[11]。由于神經網絡本身的特性，對于信息融合故障診斷而言，只要能獲得足夠精確的故障樣本數據，合理地設計網絡結構，就能得到準確的故障識別結果。

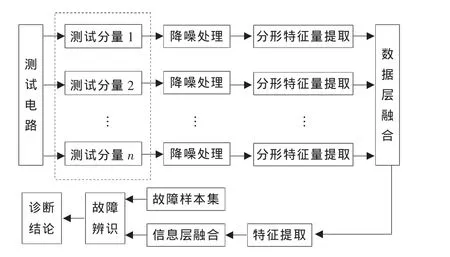
圖1 模擬電路分形特征信息融合故障診斷原理框圖

4 診斷實例

選取典型負反饋放大電路如圖2所示，各參數見圖2，電阻容差為5%，電容容差為6%。該電路雖然簡單，但是節點較多，結構復雜，單靠經驗分析排除故障存在困難。通過測試電路工作時所選支路的電流值和關鍵點電壓值兩方面的數據信息，提取分形維特征量，求出分形維數隸屬度作為BP神經網絡的輸入，準確診斷故障元器件。

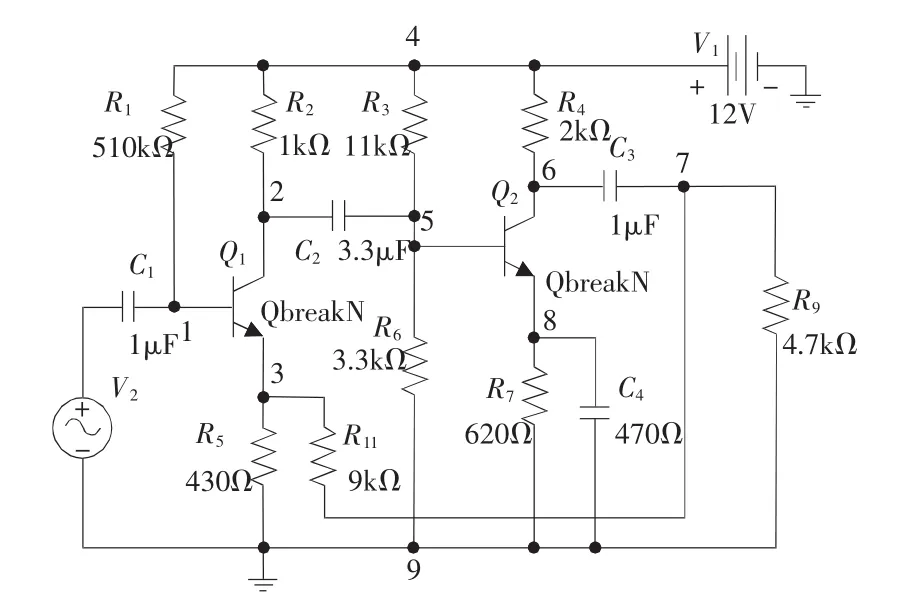
圖2 負反饋放大電路

在此，以 Q1、Q2為例，分別稱為元件 1、元件 2，神經網絡訓練期望輸出為Db（Q1）、Db（Q2），實際輸出為Db′（Q1）、Db′（Q2）。取節點3、8分別為元件1、2的工作電壓測試點，選取故障元件隸屬度函數值閾值為0.8，最大最小隸屬度函數值之差閾值為0.6，運用信息融合方法進行故障診斷。該文采用的BP網絡有4個輸入，分別是各量測參數分形維屬于故障的隸屬度值；輸出層節點數2即為故障模式的總數。綜合考慮容錯性和計算時間，隱含層節點數經過多次試驗比較后選取10個隱層神經元，學習效率取0.01，期望誤差為0.000 1，利用訓練樣本輸入BP神經網絡進行負反饋放大電路的故障診斷。表1為單一信息進行故障診斷時隸屬度分配表及故障診斷結論，表2為對表1所屬不同狀態下的電壓電流隸屬度分別進行神經網絡信息融合處理后獲得的故障診斷結論。

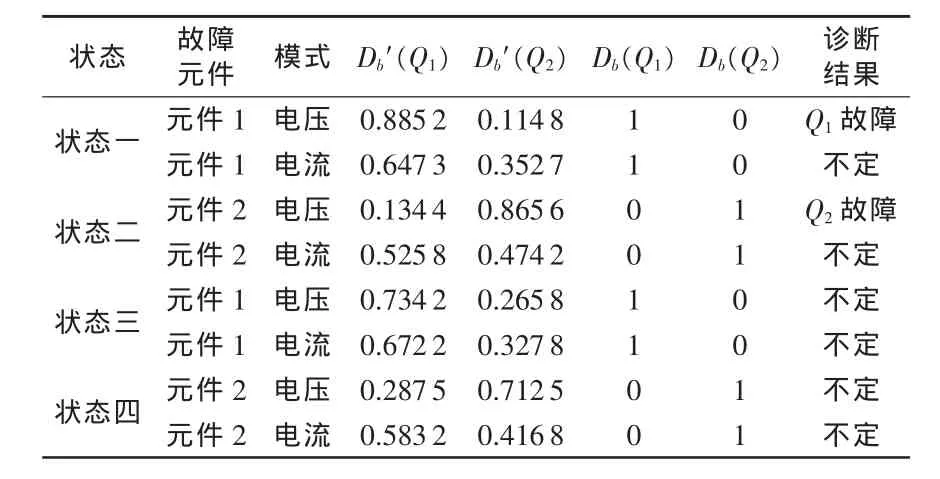
表1 單一信息診斷結論

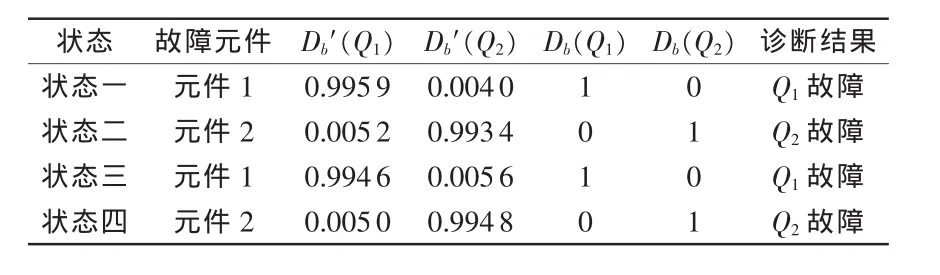
表2 BP神經網絡信息融合診斷結論

融合后的隸屬度值和單一的隸屬度值相比，增加了實際故障元件的隸屬度分配值，相對減少了其他元件的隸屬度分配值，大幅度降低待診斷電路的不確定性。從表1中可以看出，對于設定的兩種故障元件，有時候基于電壓、電流所提取的分形維數故障隸屬度值很相近，如果只用單一方式來識別，將無法確定故障元件。例如，元件2故障時，基于電流所提取的故障隸屬度值比較接近，基于電壓所提取的故障隸屬度值也不能完全識別故障，因此無法單獨判定故障元件，但經過信息融合后，元件2的隸屬度值大為提高，且與元件1的隸屬度值相差很大，就能準確判斷故障元件為Q2。通過試驗驗證，故障識別的準確率達到了100%。

由此可見，基于分形的多信息融合故障診斷方法，使實際故障元件的隸屬度值大為增加，待診斷電路的可分析性增強，故障元件定位的準確率大為提高。

5 結束語

該文研究了以分形特征為輸入量的模擬電路故障診斷方法，結果表明，該方法有效地利用了電路系統在多種狀態下的信息，將分形理論、神經網絡和信息融合技術有機地結合起來，對模擬電路的輸出響應數據提取分形特征后進行信息融合，合理地處理了模擬電路故障診斷時的不確定性，實現了故障診斷和定位。

[1]Paramanathan P，Uthayakumar R.Application of fractal theory in analysis ofhuman electroencephalographic signals[J].Computers in Biology and Medicine，2008，38（3）：372-378.

[2]李水根，吳紀桃.分形與小波[M].北京：科學出版社，2002.

[3]張 超，夏 立.發電機旋轉整流器故障的分形和動態測度診斷[J].電機與控制學報，2009，13（1）：6-10.

[4]李 沁，張勁松.基于分形的電力電子電路故障診斷[J].電力電子，2007（11）：27-30.

[5]趙 健，雷 蕾，蒲小勤.分形理論及其在信號處理中的應用[M].北京：清華大學出版社，2008.

[6]馬紅光，韓崇昭.電路中的混沌與故障診斷[M].北京：國防工業出版社，2007.

[7]張濟忠.分形[M].北京：清華大學出版社，1997.

[8]Shin K，Hammond J K，White P R.Iterative SVD method fornoise reduction oflow dimensionalchaotic time series[J].Mechanical Systems and Signal Processing，1999，13（1）：115-124.

[9]何 友，王國宏，陸大惍，等.多傳感器信息融合及應用[M].北京：電子工業出版社，2007.

[10]丁 函，劉 青.神經網絡與信息融合技術在內燃機車故障診斷中的應用 [J].現代電子技術，2008（23）：184-187.

[11]朱大奇，劉永安.故障診斷的信息融合方法[J].控制與決策，2007，22（12）：1321-1326.