基于蒙特卡羅模擬的邊坡可靠度評價＊

李 隱,鄧 建,彭 澤

(中南大學(xué)資源與安全工程學(xué)院, 湖南長沙 410083)

基于蒙特卡羅模擬的邊坡可靠度評價＊

李 隱,鄧 建,彭 澤

(中南大學(xué)資源與安全工程學(xué)院, 湖南長沙 410083)

土坡穩(wěn)定分析是十分重要的問題。定值分析法是目前工程設(shè)計中常用的分析方法,然而由于沒有考慮實(shí)際存在的不確定性,得到的結(jié)果往往不能真實(shí)反映邊坡實(shí)際狀態(tài)。邊坡可靠度分析法是在傳統(tǒng)的確定性分析基礎(chǔ)上發(fā)展起來的一種更符合客觀實(shí)際的邊坡穩(wěn)定評價方法,它建立在概率統(tǒng)計基礎(chǔ)上,以隨機(jī)變量和隨機(jī)過程為研究對象,因此更符合客觀實(shí)際。邊坡可靠度分析中的蒙特卡羅模擬,其收斂性與邊坡極限狀態(tài)方程的非線性,變量分布的非正態(tài)性等因素?zé)o關(guān),適應(yīng)性強(qiáng),是一種有效的大型復(fù)雜邊坡工程的可靠度分析與評價方法。采用條分法分析土坡穩(wěn)定性,并通過蒙特卡羅法,對邊坡可靠度進(jìn)行分析,結(jié)合工程實(shí)例,討論了土性參數(shù)的均值和變異系數(shù)對可靠指標(biāo)的影響。

不確定性;可靠度分析;蒙特卡羅法;可靠指標(biāo)

邊坡穩(wěn)定性問題一直是巖土工程學(xué)科中一項(xiàng)重要的研究內(nèi)容[1]。傳統(tǒng)的邊坡穩(wěn)定求解方法是將影響邊坡穩(wěn)定的諸因素看作確定性量,用安全系數(shù)作為衡量邊坡穩(wěn)定狀態(tài)的指標(biāo)。這種定值設(shè)計法是經(jīng)過長期工程實(shí)踐證明的一種有效設(shè)計方法。然而,邊坡工程地質(zhì)條件及巖體性質(zhì)參數(shù)具有不確定性,得出的安全系數(shù)并不能客觀地反映邊坡的真實(shí)安全程度。邊坡工程可靠度分析是把邊坡巖體性質(zhì)、荷載、地下水、破壞模式,計算模型等作為不確定量,借鑒結(jié)構(gòu)工程可靠性理論方法,結(jié)合邊坡工程的具體情況,用可靠指標(biāo)或破壞概率來評價邊坡安全度[2]。近年來,邊坡隨機(jī)可靠度分析理論與實(shí)踐得到廣泛重視和迅速發(fā)展[1～6]。目前常用的可靠度分析方法主要有一次二階矩法[4],改進(jìn)的一次二階矩法(即驗(yàn)算點(diǎn)法),JC法,隨機(jī)有限元法[5],概率矩點(diǎn)估計法[6],蒙特卡羅隨機(jī)模擬方法[7]等。祝玉學(xué)[2]等對邊坡隨機(jī)分析進(jìn)行了系統(tǒng)研究,為邊坡可靠性分析作了大量基礎(chǔ)工作。吳世偉[8]對土壩穩(wěn)定可靠度作了大量研究。姚耀武等[9]對土坡中的楔體破壞進(jìn)行了穩(wěn)定性分析。與傳統(tǒng)的確定性理論相比較,可靠性分析能更好的反映邊坡工程的實(shí)際狀態(tài),正確合理的解釋許多用確定性理論無法解釋的工程問題,但是該方法還處于研究和探索階段,還有待進(jìn)一步發(fā)展完善。

1 模擬的精度和效率

蒙特卡羅法是一種以概率和統(tǒng)計理論、方法為基礎(chǔ)的計算方法,它將所求解的問題同一定的概率模型相聯(lián)系,用電子計算機(jī)實(shí)現(xiàn)統(tǒng)計模擬或抽樣,以獲得問題的近似解,故又被稱為統(tǒng)計模擬法或統(tǒng)計試驗(yàn)法[10]。

由于隨機(jī)抽樣試驗(yàn)是概率為 Pf的伯努利試驗(yàn),N次抽樣中的失效數(shù) Nf服從二項(xiàng)分布。蒙特卡羅模擬的結(jié)構(gòu)失效頻率的均值、方差為:

而抽樣方差可表為:

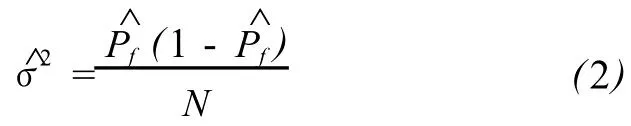
用正態(tài)分布來逼近二項(xiàng)分布,取 95%的置信度來估計失效概率,則

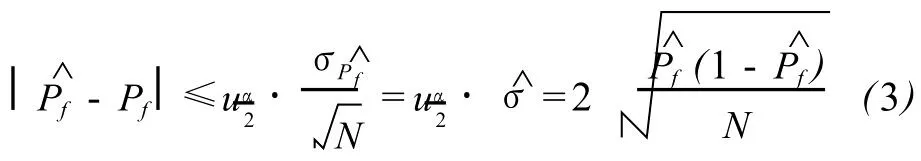
失效概率的相對誤差為:

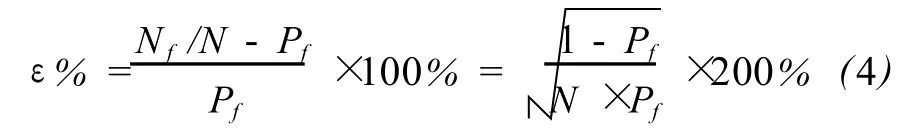
考慮到 Pf是一小量,故有:

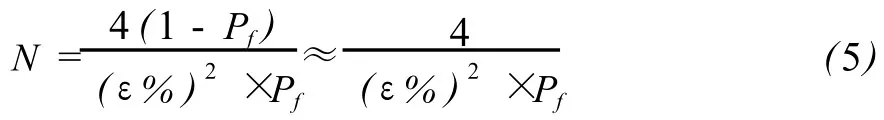
顯然,抽樣數(shù)N與結(jié)構(gòu)失效概率 Pf成反比。若ε%=20%,Pf=10-4,則 N=106才能保證模擬的精度。

2 邊坡穩(wěn)定評價標(biāo)準(zhǔn)與分析程序

依據(jù)失效概率的大小可以將邊坡分為 5種類型[2]:失效概率小于 5%的邊坡評價為穩(wěn)定;失效概率在 5%～30%之間的邊坡評價為基本穩(wěn)定;失效概率在 30%～50%之間的邊坡評價為穩(wěn)定性一般;失效概率在 50%～80%之間的邊坡評價為穩(wěn)定性差;失效概率大于 80%的邊坡評價為穩(wěn)定性極差。

GB50199-94規(guī)定水工結(jié)構(gòu)應(yīng)達(dá)到的可靠指標(biāo)見表1[11]。其中第一類破壞是指非突發(fā)性破壞,破壞前能見到明顯的征兆,破壞過程緩慢;第二類破壞是指突發(fā)性破壞,破壞前無明顯的征兆,但結(jié)構(gòu)一旦發(fā)生事故,難以補(bǔ)救和修復(fù)。

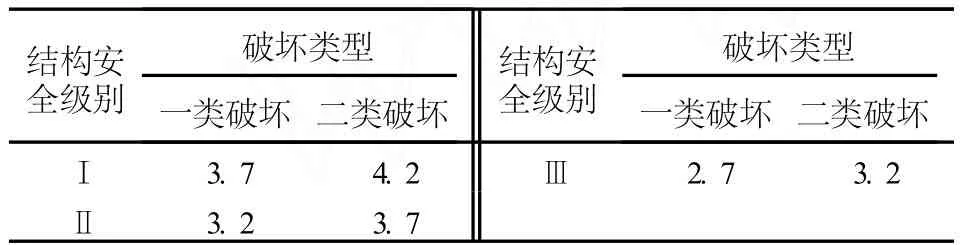
表1 目標(biāo)可靠指標(biāo)βr

根據(jù)蒙特卡羅的思路,編制邊坡穩(wěn)定計算程序,基本步驟如下:輸入各隨機(jī)變量均值,方差及分布類型;采用協(xié)方差矩陣將相關(guān)變量轉(zhuǎn)換為不相關(guān)變量;隨機(jī)產(chǎn)生一組均勻數(shù),并生成服從變量分布規(guī)律的一組參數(shù);通過逆變換生成初始變量互不相關(guān)的一組參數(shù);分別帶入 BISHOP功能函數(shù),重復(fù)計算 N次,統(tǒng)計失效次數(shù),從而計算出失效概率;檢查失效概率的穩(wěn)定性,必要時增加抽樣次數(shù) N,重復(fù)計算;計算安全系數(shù)的均值及方差,同時檢驗(yàn)其分布規(guī)律,計算邊坡的可靠指標(biāo)[12]。

在生成隨機(jī)數(shù)時可以利用MATLAB編寫 c,φ正態(tài)分布函數(shù),這種方法比較簡單、省時,由于計算機(jī)運(yùn)行能力的提高,模擬次數(shù)通常可取到十萬至數(shù)百萬次,完全能滿足計算精度的要求。

3 工程實(shí)例計算

3.1 模型建立

以大寶山邊坡為計算實(shí)例。該邊坡為土質(zhì)邊坡。本邊坡實(shí)例沒有考慮土體抗剪強(qiáng)度指標(biāo) c,φ值相關(guān)性,僅考慮計算參數(shù)的變異性及分布規(guī)律對邊坡可靠指標(biāo)和失效概率的影響。邊坡模型分為 3個土層(見圖1),土層 3中含有地下水位線,因此可以將含有水位線的土層分為兩個土層(見表2)。

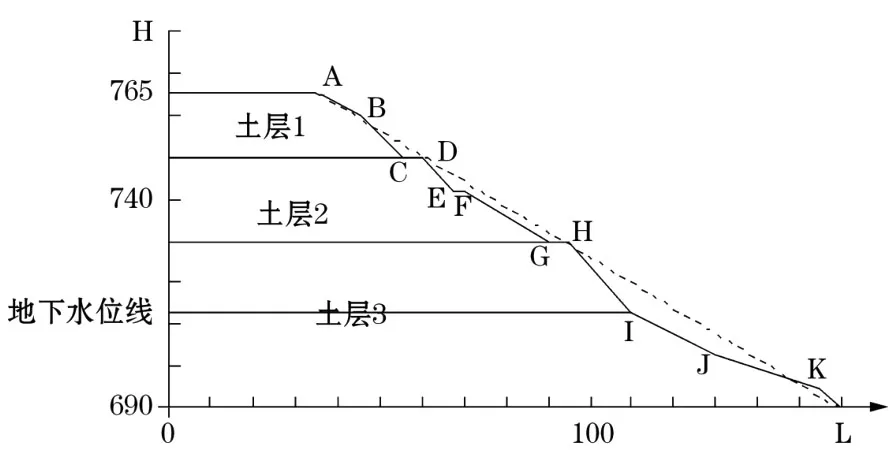
圖1 邊坡剖面

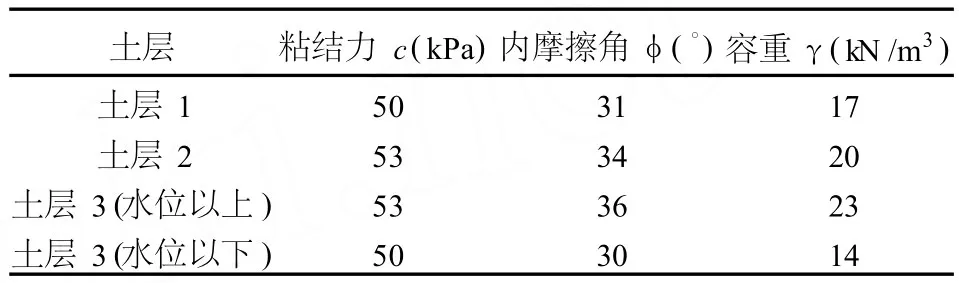
表2 土層參數(shù)

3.2 可靠度分析與評價

在邊坡可靠度分析中,土的凝聚力 c和內(nèi)摩擦角φ的影響比γ大得多,故僅取 c和φ作為基本隨機(jī)變量。根據(jù)現(xiàn)行的研究成果,c多成對數(shù)正態(tài)分布,φ多呈正態(tài)分布[13]。下面的計算和分析中取 c和φ均為正態(tài)分布。取變異系數(shù)δ=0.3,取土層 1和土層 2的 c和φ為隨機(jī)變量,分別為 c1,c2,φ1,φ2。

畢肖普法邊坡穩(wěn)定可靠性分析的功能函數(shù)為:

利用MATLAB對 4個隨機(jī)變量各自生成 N個隨機(jī)數(shù),得到 N組隨機(jī)數(shù)。分別帶入 BISHOP法的REAME程序,計算出相應(yīng)的 Fs值,代入式(6),得出 Z值。統(tǒng)計出 Z≤0的失效次數(shù) Nf,當(dāng)總次數(shù) N足夠多時,計算結(jié)束。最后由 Pf≈Nf/N計算邊坡失效概率。模擬結(jié)果列于表3。當(dāng) N足夠大時,邊坡失效概率始終保持在 Pf≈0.7%。由公式(5)可知,當(dāng) Pf≈0.7%時,N=14300才能保證模擬的精度。此時,失效概率已趨于穩(wěn)定。

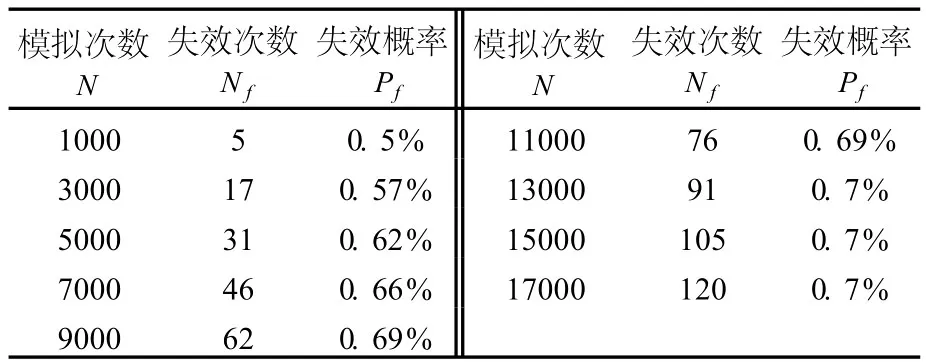
表3 統(tǒng)計失效概率

功能函數(shù)中包含有 4個相互獨(dú)立的正態(tài)隨機(jī)變量 Z=(c1,c2,φ1,φ2),邊坡安全系數(shù)可以表達(dá)為以下一個廣義的函數(shù):

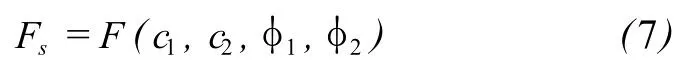
式中,c1,c2,φ1,φ2為影響邊坡穩(wěn)定的基本變量。

可靠指標(biāo)計算公式為:

式中,μF,σF分別為 Fs的均值與標(biāo)準(zhǔn)差。

依據(jù)失效概率評價邊坡穩(wěn)定,Pf≈0.7%,遠(yuǎn)遠(yuǎn)小于 5%,初步判斷邊坡穩(wěn)定。依據(jù)可靠指標(biāo),β=4.8,分別大于一類破壞的第一安全級別和二類破壞的第一安全級別,可以判定邊坡穩(wěn)定。

3.3 參數(shù)變異性對β的影響

變異系數(shù)δ=σ/μ是反映隨機(jī)變量的不確定性的一個重要指標(biāo)。為進(jìn)一步研究土性指標(biāo)的隨機(jī)性對邊坡穩(wěn)定性的影響,選取影響較大的兩個強(qiáng)度指標(biāo) c和φ的變異系數(shù)[5]進(jìn)行討論。

分析 c的變異性對β的影響時,假定δφ=0,取δc的變化范圍為 0.1～0.5。從圖2可以看出,c的變異性對β的影響顯著。δc=0.1時,β=9.2。而當(dāng)δc增大到 0.5時,β為 2.7。

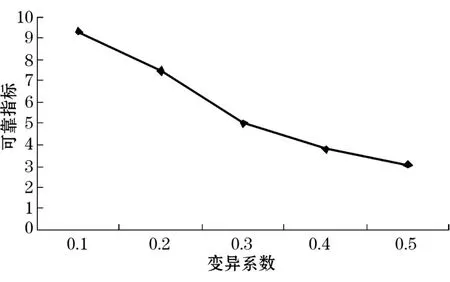
圖2 β和 c變異系數(shù)關(guān)系曲線

分析φ的變異性對β的影響時,假定δc=0,取δφ的變化范圍為 0.1～0.3。當(dāng) δφ=0.1時,β=12.3,而當(dāng)δφ=0.3時,β僅為 4.8,說明 δφ對 β影響也非常顯著(見圖3)。可靠性指標(biāo)β對土性指標(biāo)的變異性相當(dāng)敏感,當(dāng) c和φ的變異系數(shù)為不同的值時,β相差很大,規(guī)律是隨著變異系數(shù)的增大,可靠指標(biāo)變小。

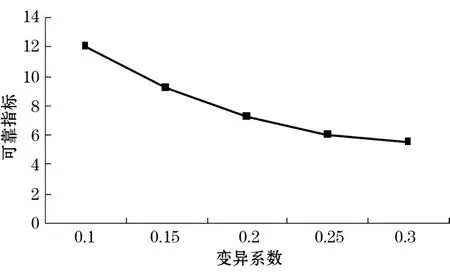
圖3 β和φ的變異系數(shù)關(guān)系曲線

4 結(jié) 論

(1)本文用土坡穩(wěn)定分析方法中最常用的條分法——簡化 Bishop法建立了可靠度分析的極限狀態(tài)方程,并與蒙特卡羅法可靠度分析程序結(jié)合起來,討論了土性參數(shù)的均值和變異系數(shù)對可靠指標(biāo)的影響。分析表明,蒙特卡羅法評價邊坡可靠度,受條件限制的影響較小,其收斂性與邊坡極限狀態(tài)方程的非線性,變量分布的非正態(tài)性等因素?zé)o關(guān),適應(yīng)性強(qiáng),是一種有效的大型復(fù)雜邊坡工程的可靠度分析與評價方法。

(2)本文對土坡可靠度分析中的一些規(guī)律性的問題進(jìn)行了深入研究,得到一些初步認(rèn)識。這對今后在土坡可靠度分析中很有參考意義,對制定按可靠度理論的土坡設(shè)計規(guī)范也具有參考價值。

[1] 陳祖煜.土質(zhì)邊坡穩(wěn)定分析(原理、方法、程序)[M].北京:中國水利水電出版社,2003.

[2] 祝玉學(xué).邊坡可靠性分析[M].北京:冶金工業(yè)出版社,1993.

[3] Li K S,Lumb P.Probabilistic design of slopes[J].Canadian Geotechnical,1987,24(4):520～535.

[4] Christian J T,Ladd C C,Baecher G B.Reliability applied to slope stability analysis[J].Journal of geotechnical engineering Division,1994,120(12):2180～2207.

[5] Deng Jian,Gu DS.A reliability based approach for evaluating slope stability under seismic loadings[A].9th International conference on structural reliability and safety[C].Rome,Italy:June 19～22,2005:175～181.

[6] 蘇永華,何滿潮.利用矩點(diǎn)估計法簡化響應(yīng)面可靠度指標(biāo)的計算[J].工程力學(xué),2007,24(7):11～15.

[7] 徐鐘濟(jì).蒙特卡羅方法 [M].上海:上海科學(xué)技術(shù)出版社,1996.

[8] 鄭 鐸,吳世偉.土壩穩(wěn)定可靠度分析方法初探[A].全國第三屆工程結(jié)構(gòu)可靠性學(xué)術(shù)會議論文集[C].南京:[s.n.],1992,612～617.

[9] 姚耀武,陳東偉.土坡穩(wěn)定可靠度分析[J].巖土工程學(xué)報,1994,16(2):80～87.

[10] Deng Jian,Gu Desheng,Li Xibing.Structural reliability analysis for implicit performance function using artificial neural network[J].Structural Safety,2005,25(1):25～48.

[11] 趙壽剛,蘭 雁,沈細(xì)中,等.蒙特卡羅法在土質(zhì)邊坡可靠性分析中的應(yīng)用[J].人民黃河,2006,28(5):65～66.

[12] 錢家歡,殷宗澤.土工原理與計算(第二版)[M].北京:中國水利水電出版社,1996.

[13] 韓玉芳,劉德輔,董 勝.邊坡整體穩(wěn)定的可靠性分析方法[J].海岸工程,2001,20(4):7～13.

高等學(xué)校博士學(xué)科點(diǎn)專項(xiàng)科研基金(200805330029).

2009-09-09)

李 隱(1984-),男,碩士研究生,安徽淮北人,主要從事巖土工程邊坡穩(wěn)定性分析,Email:jefflysci@yahoo.com.cn。