基于一次Bézier曲線和Chebyshenv神經網絡的DCT彩色盲水印算法*
陳科尹,孫樹森
(浙江理工大學 信息電子學院,浙江 杭州 310018)
隨著多媒體技術和網絡技術的快速發展與廣泛應用,對多媒體數字產品的版權進行保護已成為迫切需要解決的問題。傳統的加密技術[1,2]已經不足以解決問題,而數字水印技術[3]顯示出了其巨大的應用潛力。根據水印所嵌入域的不同,可以把數字圖像水印分為2類:一類是在空間域中嵌入水印;另一類是在變換域中嵌入水印,如DCT變換域、DFT變換域或DWT變換域等。但是,目前提出的水印算法多數是針對灰度圖像,而水印是二值圖像的,彩色圖像數字水印算法尚未得到充分研究。雖然,灰度圖像僅由代表亮度信息的像素組成,不含色彩信息,在其中嵌入水印不會產生新的顏色分量,便于操作。但現實生活中彩色圖像更為常見,所以在其中嵌入含有更豐富信息的彩色圖像水印的研究顯得更為重要和迫切。針對這種情況,本文在前人對彩色圖像水印研究[4-6]的基礎上,提出了一種基于一次 Bézier曲線和Chebyshenv神經網絡的DCT彩色圖像的盲數字水印算法。首先,把原載體彩色圖像從顏色空間RGB轉換到顏色空間HSV;然后,對彩色數字水印圖像進行三基色分離,并對每個顏色分量進行Logistic混沌置亂;最后,結合人類視覺系統(HVS)特性,把置亂的每個顏色分量的小波分解后的對矩陣元素根據一次Bézier曲線添加到原載體彩色圖像的顏色空間HSV的亮度分量V的DCT中頻子帶系數中,并且進行Chebyshenv神經網絡訓練。
1 彩色圖像顏色空間的選取
色度學理論認為,任何顏色都可以由紅(R)、綠(G)、藍(B)3種基本顏色按照不同的比例混合得到。紅、綠、藍被稱為三基色,簡稱RGB三基色。由它們組成的顏色空間,稱為RGB顏色空間。RGB顏色空間屬于線性空間坐標系,R、G、B顏色分量呈現線性相關,有利于保存圖像像素顏色之間的線性關系,但不利于人們對彩色布局直覺。HSV顏色空間是歐洲電視系統廣泛采用的顏色空間,其基本特征是將亮度信號與色度信號分開表示。V表示亮度,H和S是2個彩色分量表示色差,描述圖像色彩及飽和度的屬性。HSV顏色空間屬于非線性空間坐標系,H、S、V顏色分量呈現線性無關,空間距離符合人眼的視覺特征。因此,本文載體彩色圖像選擇HSV顏色空間,而水印彩色圖像選擇RGB顏色空間,這樣有利于提高水印算法的透明性和穩健性。
2 一次Bézier曲線的水印嵌入、提取和 Logistic混沌水印置亂
一次 Bézier曲線的定義為:p(t)=(1-t)p0+tp1,t∈[0,1],它表示一條以p0和p1為端點的線段。本文就是根據一次Bézier曲線的定義來嵌入和提取水印,水印嵌入和提取公式如下:
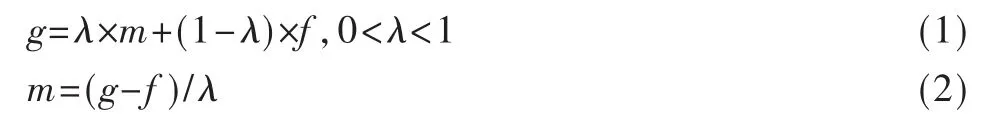
其中,g為嵌入水印后的圖像,f為原始圖像,m為水印圖像,λ為水印強度。由于一次Bézier曲線具有連續光滑和局部收斂的特性,所以按照一次Bézier曲線嵌入水印,其水印算法具有很好的透明性、可恢復性和魯棒性,并且水印信息的嵌入量比較大。
為了增強水印算法的魯棒性,水印在嵌入之前需進行置亂處理。在數字圖像的置亂方面有Logistic混沌變換、Arnold 變換、幻方、Hibert曲線、Conway 游戲、Tangram算法、IFS模型、Gray碼變換、廣義Gray碼變換等。而利用Logistic混沌變換,變換后的圖像相鄰像素的相關性更小,抗攻擊的免疫性強,具有良好的安全性。本文采用Logistic混沌變換[7]進行置亂。
3 Chebyshenv神經網絡
BP神經網絡是基于誤差反向傳播的多層前向神經網絡,已成為目前應用最為廣泛的神經網絡學習算法。通過輸入輸出樣本集的訓練,可實現從輸入到輸出的任意非線性映射,其實質是采取最快梯度下降法來實現映射關系的逼近。在原先BP 3層模型[8,9]作為神經網絡的訓練模型基礎上,本文提出了基于Chebyshev[10]的BP網絡模型(8-5-1結構),即包含8個輸入、1個5個結點隱含層和1個輸出結點的輸出層。在3層BP神經網絡中改進隱含層中的激勵函數為一組正交的Chebyshev函數,提高了隱含層和外層的逼近程度。實驗結果也證明,用改進的BP神經網絡模型作為訓練模型能更好地實現水印的盲提取。
4 水印的嵌入和提取
以 M×N的原始彩色 RGB圖像 I,大小為 p×q(p=40,q=40)的彩色水印圖像W為例描述本文的算法。
4.1 水印嵌入
(1)將I由RGB顏色空間轉換到HSV空間,取其亮度分量 V,記為 IV。
(2)將 IV分割為互不覆蓋的小塊 block(x,y),0≤x,y≤7,對 block(x,y)進行以 DCT 變換,得到 block_dct(x,y)。
(3)對彩色水印W進行三基色分離,得到 R、G、B 3個顏色分量。
(4)依次對每個顏色分量進行Logistic混沌置亂,并進行Haar小波分解,得到近似系數矩陣、水平細節系數矩陣、垂直細節系數矩陣、對角細節系數矩陣,分別記為CA1、CH1、CV1、CD1。
(5)將 CA1、CH1、CV1、CD1向 量 化 , 分 別 記 為 message_pad1,message_pad2,message_pad3,message_pad44 個向量,向量的長度為。
(6)對每個分塊 block_dct(x,y)進行 ZigZag掃描,取出中頻系數。
(7)分別取 message_pad1,message_pad2,message_pad3,message_pad4中的1個元素,嵌入到每個分塊block_dct(x,y)的中頻系數中,并且進行神經網絡訓練以及保留神經網絡訓練模型。
(8)對每個分塊 block_dct(x,y)進行反 ZigZag掃描,還原block_dct(x,y)的中頻系數的原來位置。
(9)對嵌入水印信息后的小塊 block_dct(x,y)進行反DCT 變換,記為 block′(x,y)。
(10)合并小塊 block′(x,y),記為 I′V。
(11)將 I′V轉換到 RGB顏色空間,得到嵌入水印后的圖像 I′。
4.2 水印提取
(1)將含有水印信息的圖像 I′轉換到 HSV空間,取其亮度分量 V,得到 I′V。
(2)將 I′V分割為互不覆蓋的小塊 block′(x,y),0≤x,y≤7,并進行以 DCT 變換,得到 block_dct′(x,y)。
(3)對每個分塊 block_dct′(x,y)進行 ZigZag 掃描,取出中頻系數。
(4)依據保留神經網絡訓練模型,恢復原來的每個分塊 block_dct(x,y)。
(5)對 每 一 小 塊 block_dct′(x,y),依 據 嵌 入 水 印 時的嵌入過程,進行逆運算,依次得到 message_pad′1,message_pad′2,message_pad′3,message_pad′44 個 向 量 ,向量的長度為(p,q為原水印圖像行像素數和列像素數)。
(6)分別將 message_pad′1,message_pad′2,message_pad′3,message_pad′4,還原為矩陣,得到近似系數矩陣、水平細節系數矩陣、垂直細節系數矩陣、對角細節系數矩陣:CA′1、CH′1、CV′1、CD′1。
(7)將 CA′1、CH′1、CV′1、CD′1進行 Haar 小波合成,并對合成后的分量進行Logistic混沌置換還原,將得到一個顏色分量。
(8)依據上述步驟,依次得到顏色分量 R′、G′、B′。
(9)將顏色分量 R′、G′、B′進行三基色合成,即得到提取出的水印W′。
5 實驗結果與分析
實驗采用256×256的24 bit真彩色lena圖像作為原始載體圖像如圖1所示。選用有意義的彩色圖像作為水印圖像(40×40)如圖2所示。為了客觀地評價含有水印載體圖像和水印的質量,分別采用峰值信噪比(PSNR)、圖像相似度(NC)[11]來度量。PSNR值越大,水印透明性越好;NC值越大,提取的水印越清晰,水印算法越穩健。本算法中原始載體圖像與含有水印載體圖像的峰值信噪比(PSNR)為42.2279,符合人眼視覺要求。在穩健性方面,本算法能夠較好地抵抗噪聲、剪切、旋轉、JPEG壓縮等攻擊。

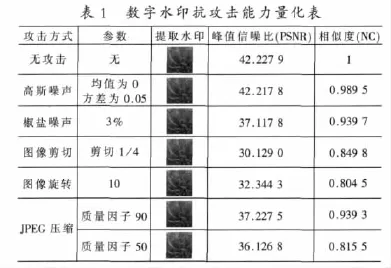
對含有水印的載體進行攻擊,測試水印系統的抗攻擊能力見表1。
從實驗結果可知,嵌入彩色水印信息后,原彩色圖像與含有水印信息后的圖像在視覺效果上沒有明顯區別,用肉眼幾乎分辨不出。這說明本算法充分利用了一次Bézier曲線的特性和人眼的視覺 HVS特性,水印的透明性相當好,不影響圖像的正常使用。本算法是利用Chebyshenv神經網絡以及Logistic混沌置亂來實現彩色圖像的水印算法,所以提取水印不需要原始圖像和原始水印,并且能夠抵抗常見的噪聲、剪切、旋轉、JPEG壓縮等攻擊。
[1]楊義先,鈕心忻.應用密碼學[M].北京:北京郵電大學出版社,2005.
[2]MAO W B.Modern cryptography:theory and practice[M].Person Education,2003.
[3]劉瑞禎,譚鐵牛.數字水印研究綜述 [J].通信學報,2000,21(8):39-48.
[4]凌賀飛,盧正鼎,楊雙遠.基于YcbCr顏色空間的二維DCT彩色圖像數字水印實用技術 [J].小型微型計算機系統,2005,26(3):482-484.
[5]郭志強,唐兵.一種彩色圖像水印方法的抗攻擊性能[J].武漢大學學報(工學版),2007,40(6).
[6]王坤,楊峰.一種改進的基于DWT的彩色圖像水印算法[J].信息技術與信息化,2009,1(53).
[7]張永紅,康寶生.基于Logistic混沌序列的圖象加密算法[J].寧夏大學學報(自然科學版),2009,30(1).
[8]王劍,林福宗.基于人工神經網絡的數字音頻水印算法[J].小型微型計算機系統,2004(11).
[9]胡金艷,張太鎰,陸從德,等.一種基于神經網絡的小波域音頻水印算法[J].陜西:西安交通大學學報,2003(4).
[10]鄒阿金,張雨濃.基函數神經網絡及應用[M].廣州:中山大學出版社,2009.
[11]楊義先,鈕心忻.數字水印理論與技術[M].北京:高等教育出版社,2006.
?

