長方形構(gòu)件的擬合研究
沈丹華 蔡榮華 林志宏 戴明如
(1.浙江省測繪大隊,浙江杭州 310030;2.浙江省溫嶺市國土局,浙江溫嶺 317500;3.浙江省溫嶺市測繪隊,浙江溫嶺 317500)
要檢測某長方形構(gòu)件,需要檢測其表面是否平整,尺寸是否符合設(shè)計要求。在其表面適當位置粘貼標志,在附近安置全站儀,觀測這些標志的空間坐標,計算其平整度和長方形的尺寸。具體步驟如圖1。
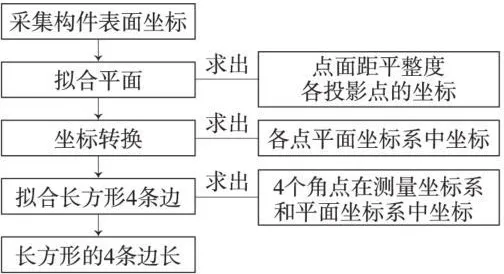
圖1 擬合空間長方形流程
1 擬合平面求平整度
圖2表示長方形在空間的位置。它與測量坐標系(o-xyh)的關(guān)系是任意的。o-h方向為垂線方向。o-xy面為水準面的切面,全站儀安置在空間長方形的旁邊,采用自由設(shè)站直接測定目標的三維坐標。
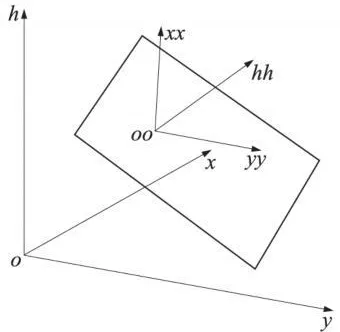
圖2 空間長方形與測量坐標系關(guān)系
由于施工誤差或觀測誤差,這些標志并不完全在同一平面內(nèi),設(shè)要擬合的平面方程為

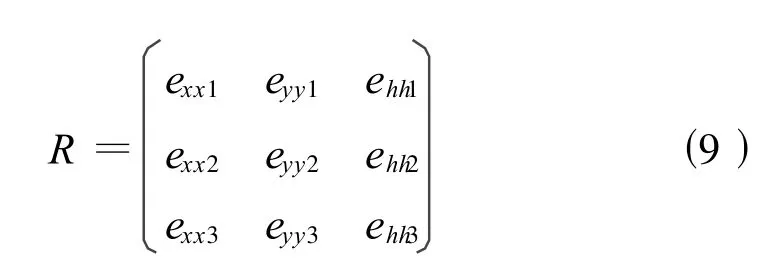
式中(a b c)T為平面的法線方向單位矢量,a>0,若a=0 則b>0,若a=0 且b=0則 c>0,a、b、c不可能同時為0。
以(xiyihi)T(i=1,2,…,n)表示觀測點坐標。
為了避免由于直線平行于某坐標軸而出現(xiàn)數(shù)值問題,求出測(xiyihi)T(i=1,2,…,n)中的3個坐標分量的最大值和最小值之差 Δx、Δy、Δh。
在 Δx、Δy、Δh 中,若 Δx 最小 ,則按 x=ay+bh+c擬合,若 Δy最小,則按 y=ah+bx+c擬合,若 Δh最小,則按h=ax+by+c擬合。
另外,也可以先將坐標分量變換至[-1 1]區(qū)間,擬合后再回代。
求得平面方程(1)后,i點至平面的距離就是誤差方程殘差

上式中的殘差通常用于表示測得平面的平整度。i點在平面上的投影點坐標(xpiypihpi)T為

投影點坐標一定滿足平面方程。
2 坐標轉(zhuǎn)換求各個點平面坐標
在求得所有測定點在平面上的投影點坐標(xpiypihpi)T(i=1,2,…,n)后,建立平面坐標系oo-xxyyhh,如圖2,此坐標系的兩個軸xx、yy處在平面內(nèi),hh軸與平面的法線方向一致,各投影點在平面坐標系中的高程hh=0。
oo點在測量坐標系o-xyh中的坐標定義為
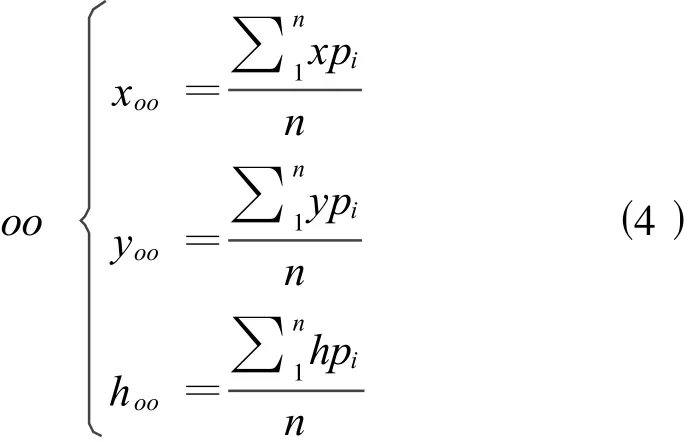
xx軸在測量坐標系o-xyh中的方向定義為oo點至面內(nèi)某點(不能是oo點)的方向,不妨設(shè)為oo點至
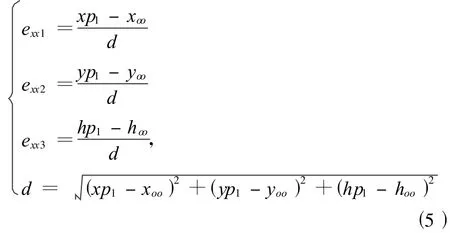
借鑒Luna24探測器和地面油田鉆井工程中穩(wěn)定器設(shè)計相關(guān)經(jīng)驗,根據(jù)鉆取采樣設(shè)備外部支撐裝置的設(shè)計需求,本文設(shè)計了一種鎖合隨動式限幅機構(gòu)。該機構(gòu)位于鉆桿的中部,在飛行工作階段主要起到鉆具的限幅作用;當鉆具鉆進到位之后,該機構(gòu)可以實現(xiàn)解鎖,并隨鉆具同步向下進尺。同時,本文基于有限元分析和地面系統(tǒng)級驗證試驗,對該限幅機構(gòu)的性能進行驗證。

yy軸在測量坐標系o-xyh中的方向是xx與hh的叉乘方向


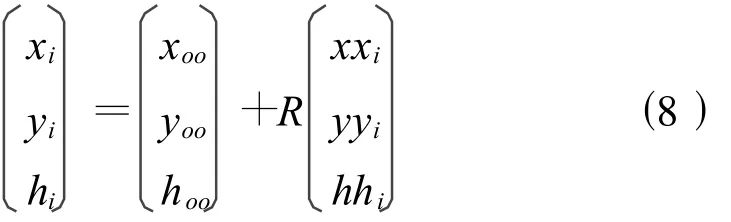
式中
由平面坐標系中坐標求測量坐標系中坐標的轉(zhuǎn)換關(guān)系為
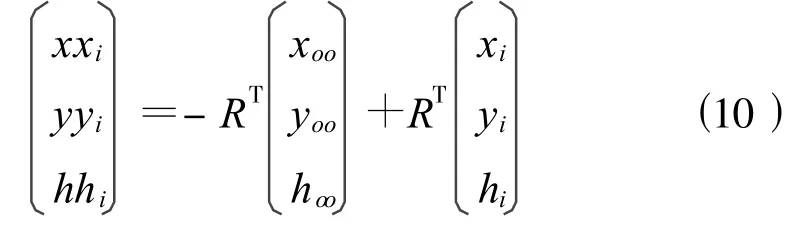
3 擬合四條邊求直角點坐標
若在長方形的四條邊上分別測定了一些點,先擬合一個平面,求出投影點坐標,將所有投影點換算至平面坐標系(如圖3所示)。)表示邊j上測定點在平面坐標系中xy平面內(nèi)的坐標。
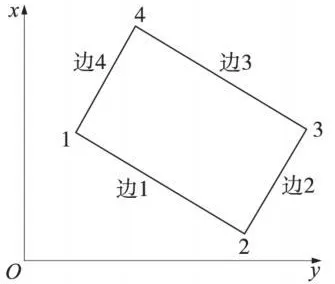
圖3 擬合長方形及其需觀測點
考察邊1上點坐標分量的范圍 Δx、Δy,若 Δx>Δy,則邊1的方程為y=ax+b1,否則方程為x=ay+b1。
對每條邊上的點列出誤差方程,如對邊2上的點
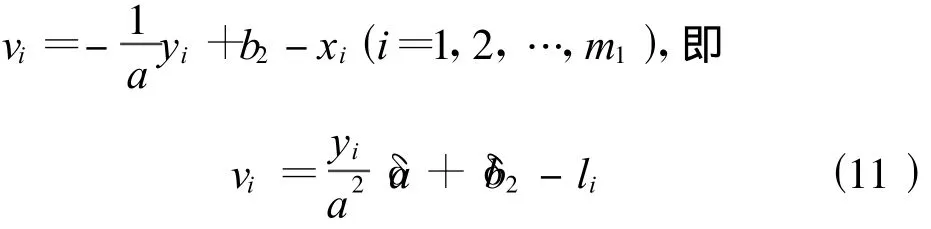
由所有點的誤差方程組成法方程求解,迭代至收斂,得到四條邊的方程(若擬合前坐標變至[-1 1]區(qū)間,則應回代)。

4 由直角點坐標求邊長
求得4個角點在平面坐標系中的坐標后,可求出長方形的邊長,按式(10)轉(zhuǎn)回測量坐標系,便可得到4個角點在測量坐標系中的坐標。
5 算例
該算例采用實測數(shù)據(jù),其中長方形的長為1 m,寬為0.667 m。實測點坐標如表1所示。
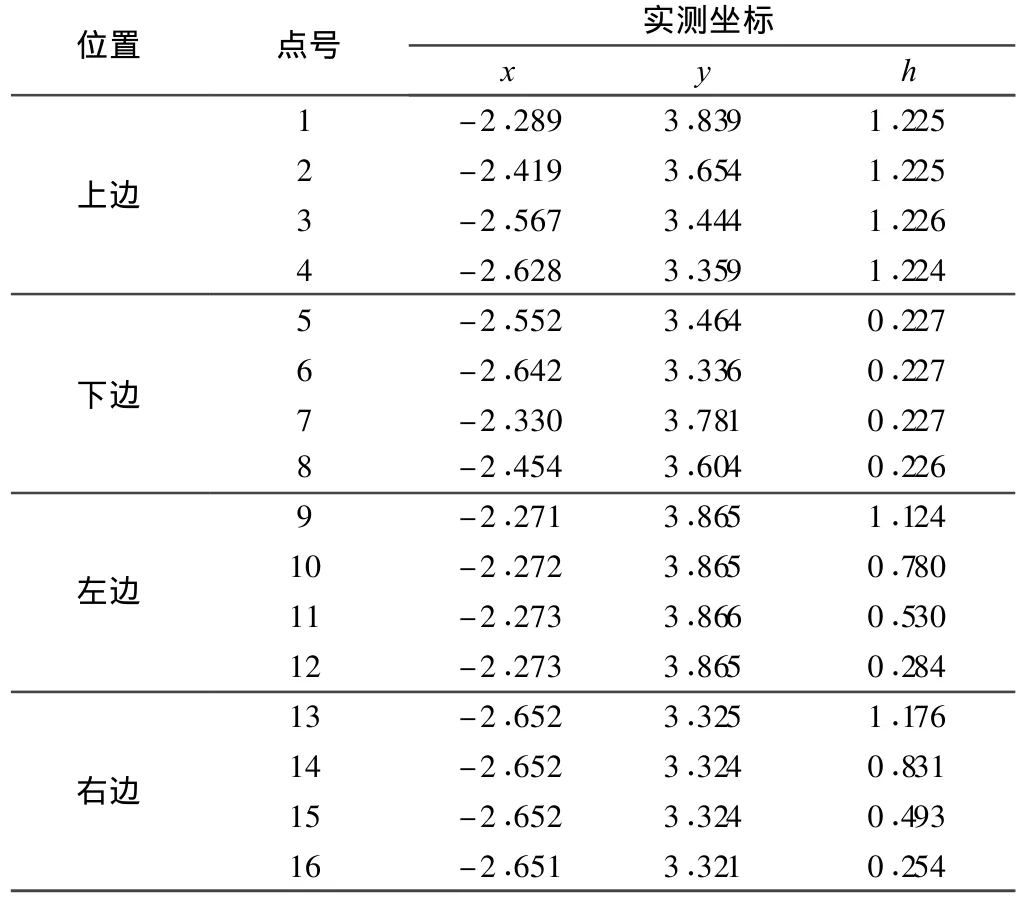
表1 各邊上實測測點坐標 m
由第2部分,式(2)擬合得平面方程的參數(shù)為

由平面實測點坐標和方程,求得各點至平面的距離Vi和投影點坐標,如表2所示。

表2 各點在平面上的投影點坐標和至平面的距離,各投影點平面坐標,觀測點至擬合直線距離 m
由表2可知,各點至平面的距離反映長方形表面的平整度,顯然只要在表面上增加觀測點的個數(shù),即可增加觀測的客觀性。由各個點的平面坐標在平面內(nèi)分別擬合直線,直線相交,求得交點的平面坐標。如表3所示。

表3 4個頂點在平面坐標系中坐標 m
擬合得四條直線方程分別為

由4個點的平面坐標分別求得邊長為:上邊0.998 293 242 594 40 m,下邊0.998 293 242 59440 m,左邊0.661 459 043 585 17 m,右邊0.661 459 043 585 17 m。將4個頂點在平面坐標系中坐標轉(zhuǎn)換回測量坐標系中,得到4個頂點在測量坐標系中坐標,如表4所示。
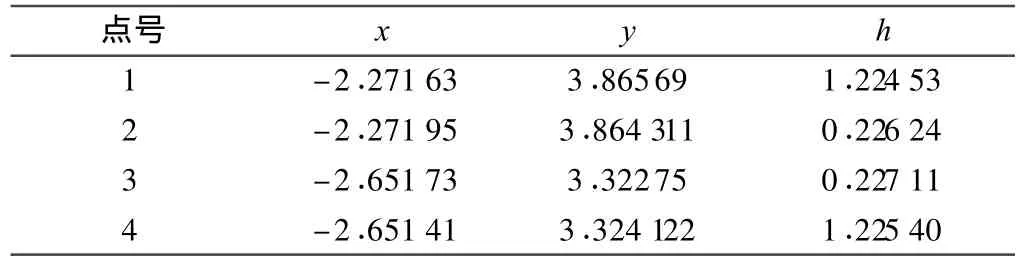
表4 4個頂點投影點在測量坐標系中坐標 m
直角點的坐標旋轉(zhuǎn)回測量坐標系,可比較直角點設(shè)計坐標與測的坐標的差別。
6 結(jié)束語
對于空間任意放置的長方形設(shè)備,利用全站儀采集了表面適當點的坐標后,可以由本文的模型算出長方形設(shè)備的各個參數(shù)及其形變量。該長方形設(shè)備檢測的方法比較全面實用,擬合過程不會損失精度。通過實例計算說明該方法可行實用,可以準確檢查工業(yè)構(gòu)件的尺寸并給出精確修改值。
[1]王解先,季凱敏.工業(yè)測量擬合[M].北京:測繪出版社,2008
[2]王解先,許 琛,陸彩萍.沉管沉放的實時監(jiān)測[J].測繪學報,2002,31:70-72
[3]陳基偉.工業(yè)測量數(shù)據(jù)擬合研究[D].上海:同濟大學土木工程學院,2005
[4]陳俊平,王解先.工業(yè)測量中的曲線擬合[J].工程勘察,2003(5):59-61

