基于性能的建筑抗震設計發展＊

于蘭蘭

(濰坊學院,山東 濰坊 261061)

基于性能的建筑抗震設計發展＊

于蘭蘭

(濰坊學院,山東 濰坊 261061)

本文以《建筑工程抗震性態設計通則》為綱,從地震設防水準、結構性態目標的確定,以及基于性能的分析方法三個方面對近幾年國內性能抗震設計的研究現狀進行了綜述。

基于性能結構抗震設計;設防水準;性能設計

0 前言

我國現行建筑抗震規范實行的是“小震不壞,中震可修,大震不倒”的三水準的設防要求。通過對汶川地震建筑物破壞情況調查統計表明,凡是按照現行抗震規范設計的建筑物倒塌的情況很少,建筑結構基本上滿足了規范規定的“大震不倒”的性態目標。但令人堪憂的是,盡管結構實現“大震不倒”,但由于其使用功能無法修復,導致巨大經濟損失。2004年6月,中國工程建設標準化協會正式批準中國工程院院士、中國地震局工程力學所研究員謝禮立主編的《建筑工程抗震性態設計通則》(以下簡稱“通則”),作為中國第一本具有樣板規范性質的建設工程抗震性態設計技術文件(CECS160:2004),在全國試行。《通則》總結了國內外的最新抗震科研成果和工程經驗,提出了有關抗震性態/性能設計、設計地震加速度、結構彈塑性地震反應、結構影響系數、結構彈塑性側移、高頻結構豎向地震反應、建筑抗震設計類別等諸多抗震設計新概念和新方法,對我國基于性能的建筑抗震設計將起到積極的推動作用。

1 性能抗震設計的主要內容

1990年代初,美國學者率先提出了基于性態結構抗震設計概念,引起了地震工程界的極大興趣,被認為是未來結構抗震設計的主要發展方向。基于性能(性態)的結構抗震設計是根據建筑物的重要性、用途或是業主的要求來確定其性能目標,提出不同的抗震設防水準并進行結構設計,最后對設計出的結構作出性能評估,看是否能滿足性能目標的要求,其目的是使設計的建筑結構在未來地震中具備預期的功能。美國加州結構工程學會的放眼21世紀委員會提出了基于性能的抗震設計(PBSD)的理論框架,性能抗震設計的主要內容包括地震設防水準的劃分,結構抗震性態水平的確定,基于性態的結構抗震設計方法[2]。

2 地震設防水平的劃分

對于基于性能抗震設計,為了實現多級設防標準,控制不同水平地震作用下結構的破壞狀態,就需要在設防地震劃分的基礎上,細化地震設防水平,并且直接采用地震動參數(目前還只限于地震加速度)來確定,美國的研究機構普遍將地震設防水準劃分為5個水平,文獻[3]在總結美國三大研究機構(SEAOC、ATC、FEMA)研究的基礎上,給出了基于性能抗震設計的地震設防水平。(見表1)

表1 基于性能抗震設計地震設防水平的劃分

我國《通則》在綜合國內外研究成果的基礎上,結合我國的實際情況,根據抗震建筑重要性類別做了分類。(見表2)

表2 《通則》中對地震設防水準的劃分

由表2可知,在《通則》中,對于重要性不同的建筑,發生某一概率水準的地震是采用不同的年限確定相應的設計地震加速度值,也就是說,列為具有較高重要性等級的建筑物考慮發生同一概率水準地震的年限應該取的更長一些,通則用這種方式來體現對建筑不同重要性等級要求的做法,顯然比現行抗震規范中簡單地增減抗震設防烈度的處理方式更為合理。

3 結構抗震性態水平的確定

結構的抗震性態水平是對設計的建筑物在可能遭受的特定設計地震作用下所規定的最低性態要求或容許的最大破壞。《通則》是根據抗震建筑的使用功能分類,對不同地震震動水平下的結構最低性態目標分為充分運行、運行、基本運行、生命安全、接近倒塌五個性能水準[1]。表3列出了《通則》中考慮的不同使用功能的建筑在三級地震震動水平下的結構需滿足的最低抗震性態要求。表3中 TMJ是由建筑重要性類別規定的年限,根據這個年限和給定的超越概率,可確定相應重要性類別的設計地震震動參數。對重要性類別為丙類的建筑,取TMJ=50年;乙類的建筑,取 TMJ=100年;甲類的建筑,取TMJ=200年。

表3 各級地震動水平下的最低抗震性態要求

4 結構的性態指標的量化

反映結構性態水平的性態指標的確定是對結構進行性態設計及評估的關鍵環節,如何科學合理的確定性態指標至關重要。目前關于結構性能水平的劃分還沒有形成統一的認識,常見的幾種性態指標的研究工作主要集中在基于結構位移的指標、基于結構損傷的指標等。

文獻[3]給出了以結構頂點位移劃分的性能水準。(見表4)

我國《通則》結合國內外的研究成果,給出了在抗震設防地震下和罕遇地震下,不同使用功能類別結構的層間位移限值,用以控制結構的性態水平。

由于地震損傷是破壞結構使用功能和導致結構倒塌的主要原因,因此基于損傷性能的抗震設計方法一直被國內外學者重視,主要從材料、構件、結構三個層次展開討論。自從Park和Ang提出了鋼筋混凝土構件地震彈塑性變形和累積滯變耗能線性組合的地震損傷模型后,國內外很多學者就致力于有關地震損傷的指標量化的研究工作。文獻[4]列出了結構的性能水準與損傷指標之間的對應關系,并對剪切型結構,提出了結構層間柱-壓彎構件三線性恢復力模型參數確定和地震損傷計算方法。文獻[5]針對彎曲型結構和剪切型結構,在Park-Ang模型的基礎上提出了基于能力譜法的地震損傷指標的計算公式。

另一種思路是從結構整體出發,通過結構非線性階段的剛度退化程度來表達結構整體的損傷程度[6]。結構損傷值可由結構遭受地震前后的剛度之比來表示。結構的剛度損傷模型可用式D=1-K1/K0來表示,式中,D為結構的損傷指數;K0為結構遭受地震前,采用推倒分析所得的基底水平力-頂部位移圖中的初始斜率;K1為遭受地震后基底水平力-頂部位移圖中的初始斜率。此方法的優點是結構損傷指數D不需要通過構件損傷指標的加權處理來獲得,從而避免了加權處理方法中權系數確定的難點,同時結構在不同的加荷狀態均可計算損傷值,而無需猜測最大位移或結構臨近倒塌時的變形。

文獻[4]基于Park-Ang模型,得出鋼筋混凝土結構的性態水平與損傷指數之間的定量關系,基本完好的損傷指數為0-0.20,輕微破壞為0.20-0.40,中等破壞為0.40-0.60,嚴重破壞為0.60-0.90,倒塌為＞0.90。

5 基于性態的結構抗震設計評估方法的研究

實驗證明,結構的性態水平與結構的層間位移角具有相關性,層間位移角能夠反映鋼筋混凝土框架結構層間各構件變形的綜合結果和層高的影響。文獻[7]建立了RC框架下層架位移與構件變形之間的關系,研究了柱的變形特點和影響因素。目前,以層間位移角為量化指標的性態設計被廣泛研究[8-9]。

基于位移法的性能設計的一般思路為在結構自振周期相等的前提下,首先將多自由度體系等效為一單自由度體系來簡化計算,求等效單自由度體系的最大位移反應Δd,然后利用位移反應譜確定與最大位移反應Δd相對應的有效周期 Te。利用 Te推導出 Ke后再根據Vb=KeΔd求得等效單自由度體系的基底剪力Vb,再進一步反推導得到多自由度體系各個質點的水平地震作用,以利于結構的抗震設計計算。

基于位移的性能指標一般通過對結構進行非線性靜力分析方法(Pushover分析方法)和非線性動力分析方法得到。非線性動力分析方法的優點是能充分反映地震震動三要素(頻譜、震幅與持時)的影響,但該法較復雜,工作量較大,在地震波選取、恢復力模型、結構計算模型等方面存在不足,使其在工程中推廣應用受限制。而基于Pushover分析的非線性靜力分析方法由于具有簡單和操作性強的優點而被國內外廣泛研究,基于Pushover分析的抗震評估方法主要有能力譜法、等效位移系數法以及N2方法等。

能力譜法的思路是首先假定地震荷載的分布模式,然后單調加載直至結構倒塌或進入不穩定狀態,并根據剛度的變化隨時調整荷載分布,同時記錄結構的頂點位移和底部剪力值。然后再分別除以相應的振型參與系數和有效振動質量,得到譜加速度-譜位移表示的結構能力曲線。再將規范給出的設計反應譜轉化成譜加速度-譜位移表示的結構需求譜曲線。二者的交點即為結構在地震中可能達到的最大位移響應(見圖1)。然后再將其轉化成頂點位移,將等效單自由度體系(SDOF體系)頂點位移轉化為多自由度體系(MDOF體系)頂點位移,從而判斷出結構的抗震性能。若出現能力譜與需求譜不相交的情況,則說明結構無法抵抗假定的地震作用,設計不合理,須重新選擇結構體系。

目前,這種方法已經應用于2000年日本的新規范中。但此方法對短周期結構分析精度尚可,但對長周期結構來說,由于高振型的影響可能會帶來較大的誤差。鑒于此,Chopra和 Geol借助彈性體系振型分解反應譜方法的思路提出的模態Pushover法就是其中一種較好的改進[10]。這種方法保留了概念的簡潔性,側向力或側向位移分布保持不變,而且在估算結構地震需求方面具有較好的精度。葉列平充分發揮圖表法在確定性態點時直觀性的優點,提出了一種“能力-需求曲線”的方法,解決了地震位移需求確定過于復雜和長周期結構可能會產生較大誤差的不利問題[11]。另外,文獻[12]在模態Push-over法的基礎上,通過算例驗證了利用延性需求譜求解結構位移需求是一種具有一定精度可為工程接受的簡便方法,在基于性能的抗震設計中具有較好的應用前景。

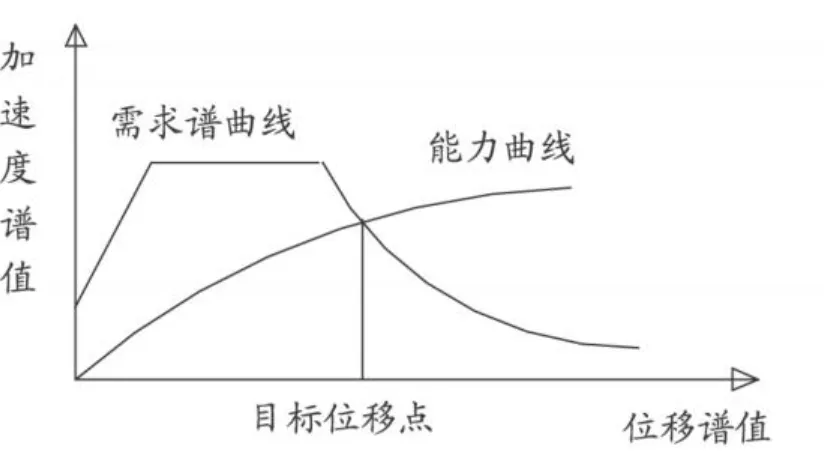
圖1 能力譜方法

等效位移系數法的基本思路是結構目標位移通過公式(1)確定。

式中,C0為SDOF體系和MDOF體系頂點位移(譜位移)之間的修正系數,可以為控制點出第一振型參與系數或達到目標位移時變形形狀對應的振型矢量計算得到的參與系數;C1為最大非線性位移期望值與線性位移的比例因子,C1一般大于1.0但不超過1.5;C2為滯回環形狀對最大位移反應的影響系數,按結構形式和建筑物重要性的不同來取值;C3為P-△效應對位移反應的影響系數對于屈服后的結構,值取1.0;Sa為在實際自振周期和阻尼比的譜反應加速度;T0為實際自振周期。求得目標位移,然后再按照推導出的需求譜來估計相應性態水平的加速度,從而進行結構地震震動輸入進行構件設計。

N2方法最早由Fajfar提出[13],思路和能力譜方法類似,即首先通過非線性靜力分析將MDOF體系轉化成等效的SDOF體系進行分析,得出反映不同性態水平的體系反應,從而進行基于性能的結構抗震設計。在此基礎上,文獻[14]提出了一種適用于不規則橋梁性態設計的N2方法,將Pushover法與非線性時程分析法結合起來對模型復雜的橋梁結構進行了分析,這同時對較為復雜的建筑結構分析提供了一種可供參考的思路。

6 可靠度概念的引入

性能指標與性能水準是一一對應的,即每一級性能目標都代表一種破壞程度。而實際工程中,由于地震作用的隨機性,場地條件、結構選型、構件截面尺寸、材料強度等因素的不確定性,某一性能指標很難百分百地代表結構的性能水準。因此,將性能指標賦予一定的概率意義,更能科學合理地解決問題,即性能指標能夠多大程度地代表性能水準的問題。吳波[15]提出了直接基于位移可靠度的抗震設計中層間目標位移代表值的確定方法,從而將可靠度理論與基于性能的抗震設計方法結合起來。

7 結論及展望

隨著我國《通則》的試用,基于性能的抗震設計必將得到越來越廣泛的研究和應用。基于性能的抗震設計關鍵問題是性能指標的確定以及基于性能抗震方法的實用性研究。由于不同結構形式、不同材料類別之間的差異,相同水平的地震激勵下所表現出來的性能水平有很大差異,量化對應各種結構性態指標的工作仍需深入的研究和討論。而目前多數性能目標的研究大多都基于規則結構的研究,而對于不規則結構形式,比如高層框剪結構、隔震結構等的性態指標尚待進一步深入研究。

[1]謝禮立.建筑工程抗震性態設計通則[M].北京:中國計劃出版社,2004.

[2]Miranda E.Seismology committee of the structure engineering association of california[C]//Vision 2000 Committee:Performance-based engineering of building.Oakland:Wileylnc,1995.

[3]馬宏旺,呂西林.建筑結構基于性能抗震設計的幾個問題[J].同濟大學學報,2002,30(12):1429-1434.

[4]歐進萍,何政.鋼筋混凝土結構基于地震損傷性能的設計[J].地震工程與工程振動,1999,19(1):21-30.

[5]何政,歐進萍.鋼筋混凝土結構基于改進能力譜法的地震損傷性能設計[J].地震工程與工程振動,2000,20(2):31-38.

[6]Ghobarah A,Abou-Elfath H,Biddah A.Response based damage assessment of structures[J].Earthquake Engineering and Structural Dynamics,1999,28(1):29-104.

[7]羅文斌,錢稼茹.鋼筋混凝土框架基于位移的抗震設計[J].土木工程學報,2003,36(5):22-29.

[8]梁興文,黃雅捷,楊其偉.鋼筋混凝土框架結構基于位移的抗震設計方法研究[J].土木工程學報,2005,38(9):53-60.

[9]田野,梁興文.鋼筋混凝土框架結構直接基于位移的抗震設計[J].世界地震工程,2005,21(2):64-69.

[10]Chopra A K,Goel R K.A modal pushover analysisp rocedure for estimating seismic demands for buildings[J].Earthquake Engineering and Structural Dynamics,2002,31(2):561-582.

[11]葉列平.基于性能P位移的能力-需求曲線設計方法[J].工程抗震與加固改造,2009,31(3):50-55.

[12]周定松,呂西林.延性需求譜在基于性能的抗震設計中的應用[J].地震工程與工程震動,2004,24(1):30-38.

[13]Fajfar P,Fischinger M.N2-a method for non-linear seismic analysis of regular buildings[J].Proceedings of the Ninth World Conference in Earthquake Engineering,1998,5:111-116.

[14]王東升,王國新,艾慶華.不規則鋼筋混凝土梁橋抗震性能評價的N2方法[EB/OL].(2004-01-08). http://www.paperedu.cn/paper_d07q5c.

[15]吳波,李藝華.直接基于位移可靠度的抗震設計方法中目標位移代表值的確定[J].地震工程與工程振動,2002,(6):44 -51.

(責任編輯:肖恩忠)

2010-03-22

于蘭蘭(1980-),女,山東海陽人,濰坊學院建筑工程學院助教。研究方向:建筑結構、建筑概念設計。

TU311 文獻標識碼:A 文章編號:1671-4288(2010)04-0124-04