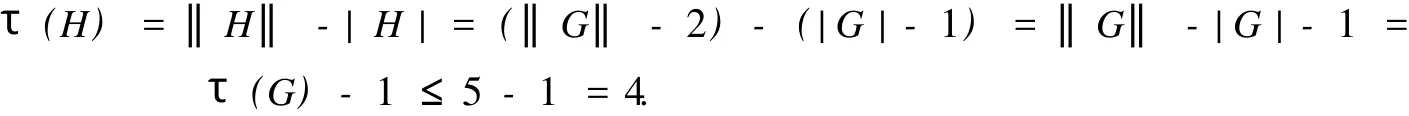關(guān)于完全可定向圖的一個注記＊

許豐偉, 王維凡

(浙江師范大學數(shù)理與信息工程學院,浙江金華 321004)

本文僅考慮有限簡單圖.給定一個圖 G,用 V(G),E(G),|G|,‖G‖,Δ(G)和δ(G)分別表示它的頂點集合、邊集合、頂點數(shù)、邊數(shù)、最大度和最小度.G的圍長是指圖 G中最短圈的長度,用 g(G)表示;對于一個頂點 v∈V(G),用 d(v)表示 v在 G中的度,若 d(v)=k,則稱 v為 G的一個 k-點;用 N(v)表示 v的所有鄰點的集合;對于 S?V(G),用 G[S]表示 S在 G中的導出子圖;圖 G的一個正常 k-染色是指有一個從 V(G)到{1,2,…,k}的映射 f,使得當 x和 y相鄰時,有 f(x)≠f(y);G的色數(shù)定義為 G的所有正常 k-染色中最小的 k值,記為χ(G).本文其他未加說明的符號和術(shù)語見文獻[1].

給圖 G的每一條邊指定一個方向后得到一個有向圖,若此有向圖不存在有向圈,則稱此有向圖為 G的一個無圈定向;設 D是 G的一個無圈定向,若改變D中的一條弧的方向會產(chǎn)生有向圈,則稱這條弧為D的相依邊,用 d(D)表示 D中相依邊的條數(shù);給定一條相依邊,以 x為尾,y為頭,那么 D中必包含一條長度至少為 2的從 x到 y的有向路.用 dmin(G)和 dmax(G)分別表示 G的所有無圈定向中相依邊數(shù)的最小值和最大值.若對滿足 dmin(G)≤k≤dmax(G)的所有 k,都存在 G的無圈定向 D,使得 d(D)=k,則稱 G為完全可定向的.

對于圖的完全可定向性,目前已有一些研究成果.例如,文獻[2]給出了 dmax(G)=‖G‖-|G|+c,其中 c表示 G的連通分支數(shù),同時證明了當χ(G)

給定一個連通圖 G,令τ(G)=‖G‖-|G|.如果τ(G)=-1,則 G是一個樹;如果τ(G)=0,則 G是一個單圈圖.由τ(G)的定義知,dmax(G)=‖G‖-|G|+1=τ(G)+1.綜合文獻 [2,4]的結(jié)果知,當dmin(G)不超過 1時 G是完全可定向的.對照這個結(jié)果,人們自然要問:當 dmax(G)至多為何值時 G是完全可定向的?本文完全回答了這個問題:當 dmax(G)≤6時,G是完全可定向的.

在給出主要結(jié)果之前,先引入一些有用的引理.

引理 1[7]設 G1,G2,…,Gk是 G的連通分支,若 Gi是完全可定向的 (i=1,2,…,k),則 G也是完全可定向的.

引理 2[8]設 v∈V(G)是 G的一個割點,G-v的連通分支的頂點集為 V1,V2,…,Vm,令 Gi是Vi∪{v}(i=1,2,…,m)的導出子圖.若 Gi(i=1,2,…,m)是完全可定向的,則 G也是完全可定向的.

引理 3[7]設 v是圖 G的一個度至多為 2的頂點.若 G-v是完全可定向的,則 G也是完全可定向的.

引理 4[8]設 v是圖 G的一個 3-點,且 v的鄰點中至少有 2個相鄰.若 G-v是完全可定向的,則 G也是完全可定向的.

引理 5[8]若Δ(G)≤3,則 G是完全可定向的.

定理 1 若τ(G)≤5,則 G是完全可定向的.

證明 對 G的頂點數(shù)進行歸納證明.如果 |G|≤4,那么Δ(G)≤3,由引理 5知,G是完全可定向的.假設 G是一個滿足 |G|≥5且τ(G)≤5的圖,則由引理 1知,可以考慮 G是連通圖.進一步,由引理 2知,可假設 G是 2-連通的,因此δ(G)≥2.首先證明斷言 1.

斷言 1 G滿足下面 2個性質(zhì):

(1)若δ(G)≥4,則 G? K5;

(2)若 δ(G)=3,則 |G|≤10.

證明 因為τ(G)=‖G‖-|G|,所以‖G‖=τ(G)+|G|.由握手定理得

為了完成定理 1的證明,首先假設δ(G)=2,則 G有一個 2-點 v.設 H=G-v,那么 |H|=|G|-1,且

由歸納假設知,H是完全可定向的.由引理 3知,G也是完全可定向的.

其次,假設δ(G)≥4.由斷言 1(1)知,G?K5.由文獻[5]知,G是完全可定向的.

最后,假設δ(G)=3.由斷言 1(2)知,|G|≤10.如果Δ(G)=3,亦即 G是一個 3-正則圖,則由引理 5可斷言 G是完全可定向的.于是,假設Δ(G)≥4.這就隱含著 |G|≠10,否則 30=3|G|≤

如果χ(G)

斷言 2 G有一個 3-點 v,使得 v的 3個鄰點中至少有 2個是相鄰的.

當τ(G)=5時,‖G‖=|G|+τ(G)=7+5=12.假設 V(G)={u1,u2,…,u7}滿足 3≤d(u1)≤d(u2)≤…≤d(u7)≤6.此時,注意到 4≤Δ(G)≤6.

若Δ(G)=6,則 d(u7)=6,d(ui)=3,i=1,2,…,6.容易看到,u7的鄰點中必有 2個是相鄰的,故斷言 2成立.

若Δ(G)=5,則 d(u7)=5,d(u6)=4,d(ui)=3,i=1,2,…,5.因此斷言 u7的鄰點中必有 2個是相鄰的,否則‖G‖≥5+2·5=15,矛盾.由于在這 2個相鄰的頂點中至少有 1個是 3-點,故斷言 2成立.

若Δ(G)=4,則 d(u7)=d(u6)=d(u5)=4,d(u4)=d(u3)=d(u2)=d(u1)=3.首先假設 u7有一對鄰點相鄰.若這對相鄰的頂點中至少有 1個是 3-點,則斷言 2成立.否則,假設 N(u7)={u3,u4,u5,u6},u5u6∈E(G),u3u4,u3u5,u3u6,u4u5,u4u6?E(G).因為 d(u5)=d(u6)=4且 d(u3)=d(u4)=3,所以{u3,u4,u5,u6}中的每個點必須分別與 u1和 u2相鄰,于是 d(u1)≥4且 d(u2)≥4,與假設矛盾.其次假設 u7的任一對鄰點均不相鄰.因為δ(G)=3,‖G‖=12,所以容易推出 G是完全二部圖 K3,4,與假設矛盾.故斷言 2成立.

(3)|G|=8

當τ(G)=5時,顯然,‖G‖ =|G|+τ(G)=8+5=13,4≤Δ(G)≤5,G至少有 6個 3-點.假設V(G)={v1,v2,…,v8},使得 3=d(v1)=d(v2)=…=d(v6)≤d(v7)≤d(v8)≤5.若 G含有一個 3-圈 C,則 C上必有一個 3-點滿足斷言 2.于是,假設 G不含 3-圈,即 g(G)≥4.

如果 d(v8)=5,那么 d(v7)=3.假設 v8的鄰點集合為 N(v8)={v3,v4,…,v7}.若{v3,v4,…,v7}中至少有 2個頂點是相鄰的,則斷言 2成立.否則,{v3,v4,…,v7}中的每個頂點必分別與 v1和 v2相鄰,導致‖G‖≥5+5·2=15,矛盾.如果 d(v8)=4,那么 d(v7)=4.假設 N(v8)={v1,v2,v3,vk},其中 k∈{4,5,6,7}.若 v1,v2,v3,vk中至少有 2個頂點相鄰,則斷言 2成立.于是,假設 v1,v2,v3,vk是互不相鄰的,并令 S={v4,v5,v6,v7}{vk}.因為 ‖G‖=13,所以導出子圖 G[S]至多包含 1條邊,進一步,G[S∪{v8}]至多包含 1條邊.用 1,2染 S∪{v8}中的頂點,用 3染 N(v8)中的頂點,得到 G的一個正常3-染色,于是χ(G)≤3,與假設χ(G)≥g(G)≥4矛盾.故斷言 2成立.

(4)|G|=9

由斷言 2知,G有一個 3-點 v.設 H=G-v,那么 |H|=|G|-1,且

由歸納假設知,H是完全可定向的.由引理 4知,G也是完全可定向的.定理 1證畢.

因為 dmax(G)=‖G‖-|G|+1=τ(G)+1,所以由定理 1可得推論 1.

推論 1 若 dmax(G)≤6,則 G是完全可定向的.

推論 1中的條件 dmax(G)≤6是最好可能的,因為對于滿足 dmax(K3(2))=7且 K3(2)不是完全可定向的.這就從相依邊數(shù)最大值的角度完全刻畫出圖的完全可定向性.

[1]Bondy J A,MurtyU S R.Graph Theory[M].Berlin:Springer,2008.

[2]FisherD C,Fraughnaugh K,LangleyL,et al.The number of dependent arcs in an acyclic orientation[J].J Combin Theory:B,1997,71(1):73-78.

[3]Gr?tzsch H.Ein Dreifarbensatz für dreikreisfreie Netze auf der Kugel[J].W iss ZMartin-Luther Univ Halle-W ittenbergMath-Nat Reihe,1959(8):109-120.

[4]LaiH H,Lih KW,TongLida.Fullyorientabilityof graphswith atmostone dependentarc[J].DiscteteApplMath,2009,157(13):2969-2972.

[5]WestD B.Acyclic orientations of complete bipartite graphs[J].DiscreteMath,1995,138(1):393-396.

[6]Lih KW,Lin Chenying,TongLida.On an interpolation property of outerplanar graphs[J].Disctete ApplMath,2006,154(1):166-172.

[7]Lai H H,Chang G J,Lih KW.On fully orientability of 2-degenerate graphs[J].Infor m ProcessLett,2008,105(5):177-181.

[8]Lai H H,Lih KW.On preserving full orientability of graphs[J].European J Combin,2010,31(2):598-607.

[9]Chang G J,Lin Chenying,TongLida.Independent arcs of acyclic orientations of completer-partite graphs[J].DiscreteMath,2009,309(13):4280-4286.