吡啶鹽衍生物分子非線性光學性質的理論研究*

施 菊，朱 利，崔一平

(東南大學電子科學與工程學院先進光子學中心， 南京210096)

有機非線性光學(NLO)材料因其結構易裁剪性、電子響應快、光損傷閾值高、介電常數低和非線性極化率較大等優點，在全光器件、光存儲和光信息處理等領域起著越來越重要的作用[1-2]。研究表明，有機分子的離域π電子以及分子內電子給體(D)和電子受體(A)間的電荷轉移(CT)對非線性極化率起決定作用[3]，從分子角度設計和合成具有大的一階超極化率β 的分子成為當前研究的熱點。吡啶陽離子是最強的吸電子基團之一，在電子給體和共軛結構類似的情況下，吡啶鹽衍生物的β 一般要比非離子型的中性分子高出幾倍[4]，因此引起了實驗和理論工作者的極大興趣。

一般，實驗研究NLO性質主要是通過電場誘導二次諧波(EFISHG)、超瑞利散射(HRS)等方法。但是，由實驗得到的超極化率都是動態超極化率，需要通過相應的模型(如二能級模型)轉換才能近似求得靜態超極化率[5]；另一方面，實驗中往往要利用共振增強效應，共振增強雖然使得超極化率大大增加，但是共振作用往往使參與作用的光場強度嚴重減弱以及光學材料的損耗增大[6]。研究證明，量子化學從頭算方法對有機分子NLO系數計算能夠取得很好的結果[7]。

理論上用量子化學研究非線性光學性質主要是態求和(SOS)方法，有限場(FF)方法和耦合微擾Hartree-Fock(CPHF)方法[8]。本文利用Gaussian03軟件[9]的耦合微擾Hartree-Fock(CPHF)方法計算了體系的靜態超極化率，另外利用CIS方法計算了體系的激發態，得到體系的優化構型、電荷分布、偶極距、前線分子軌道和吸收光譜等，從而深層次研究結構和非線性光學性質之間的關系。

1 理論方法

當分子受到激光照射時，分子在外場作用下強極化、產生誘導偶極子。在靜態外場作用下，分子偶極矩μ可以唯象的展開成外電場E的泰勒級數[10]：

其中， λ， μ， ν和ρ表示直角坐標分量，例如x， y，z；μ， α， β和γ分別為無外場作用時的偶極矩、線性極化率、一階超極化率和二階超極化率。

在靜態外場作用下，一階超極化率β是分子偶極矩μ對于外電場E的二階導數；又因為分子偶極矩μ是能量ε對于外電場E的一階導數，所以一階超極化率β是能量ε對于外電場E的導數，

因此，一階超極化率β 的各個張量元可以表示為：

為了能跟實驗值比較，可用式(3)和式(4)將β的各個張量元轉化β的分量和標量值[11]：

2 結果與討論

2.1 優化構型

本文在6-31G(d)基組水平上采用HF方法在氣態條件下全優化吡啶鹽衍生物分子陽離子，分別為4-(4-二甲基氨基-苯乙烯基)-N-甲基吡啶(R1)、2-(5-久洛尼啶)-亞乙烯基-N-甲基吡啶(R2)和4-[4-(N， N-二苯基)-苯乙烯基]-N-甲基吡啶(R3)，如圖1所示。這三個分子具有相同的共軛橋π(乙烯基)和受體A(吡啶環)，唯一不同的只是給體D分別由三苯胺、久洛尼啶環、二甲基苯胺組成，屬于典型的D-π-A型結構分子。頻率計算后，發現沒有虛頻，說明得到的是基態穩定構型。計算結果顯示， R1中氨基N原子上的兩個甲基與分子骨架不在一個平面；R2通過兩個六元環將給電子基團固定到苯環上，有效地提高了分子的平面性；R3中氨基N原子上兩個苯環由于空間位阻作用而完全偏離分子平面，整個分子的平面性最差。但這些分子整體骨架結構呈良好的平面性，因此有利于分子內電荷的傳遞。

圖1 吡啶衍生物分子結構

2.2 電荷分布與偶極矩

根據Mulliken電荷分布計算了體系的基態電荷分布qg、偶極矩μg和第一激發態電荷分布qe、偶極矩μe，表1列舉的是各不同給體的電荷分布與偶極矩。由表1可以看出，與中性分子不同，這類離子性分子在基態具有更大的極性，表現在與激發態相比，基態具有更大的偶極矩，因此基態和激發態之間的偶極矩差為負值，預示了若在溶液中將隨著溶劑極性的增強而逐漸使其吸收光譜藍移。觀察各給體基態電荷到激發態電荷改變Δqeg=qe-qg的大小，得到各給體的給電子能力大小次序為：三苯胺＞久洛尼啶環＞二甲基苯胺，這與各分子Δμeg=μe-μg的順序一致，所以給體的給電子能力的強弱是決定Δμeg大小的主要因素。

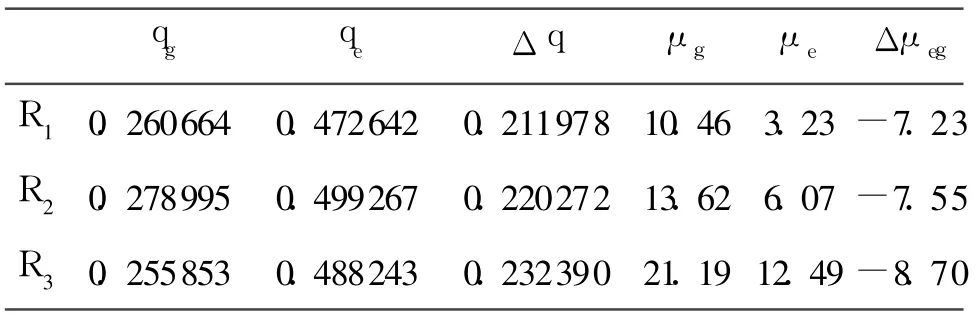
表1 給體基態和激發態電荷分布(1.6022×10-19C)及偶極矩(Debye)

2.3 分子前線軌道

圖2 給出了體系前線分子軌道分布情況，由圖2可見，三個分子具有相似的HOMO和LUMO軌道電子云分布，分子的最高占據軌道(HOMO)電子云主要分布在三苯胺、久洛尼啶環、二甲基苯胺基團以及和其鄰近的苯環上，最低空軌道(LUMO)的電子云主要分布在吡啶環以及和其鄰近的苯環上，其他原子相對較少。電荷轉移主要從電子給體(三苯胺、久洛尼啶環和二甲基苯胺和與其鄰近的苯環)到電子受體(吡啶環和其鄰近的苯環)。比較它們的前線分子軌道發現：隨著給體的給電子能力的增強，電荷轉移的能力也隨之增強。

圖2 分子前線軌道電子分布

表2列出了各個分子的前線分子軌道的能級分布情況，發現最高占據軌道(HOMO)和最低空軌道(LUMO)之間的能隙基本上是隨給體的給電子能力的增強而減小。盡管三苯胺的給電子能力強于久洛定環，但是因為三苯胺上兩個苯環偏離分子平面，阻礙了電荷從 HOMO到 LUMO的躍遷， 從而 R3的HOMO與LUMO之間的能隙相對R2增大。

表2 分子前線軌道的能級分布(eV)

2.4 光譜分析

在優化構型的基礎上采用CIS方法計算分子的激發態，得到基態到各個激發態(選取第一激發態為例)的激發能、躍遷偶極距、最大吸收波長、振子強度和軌道成分，見表3。計算結果表明，所有分子的激發主要源于HOMO到LUMO軌道的躍遷，這個躍遷對最大吸收波長貢獻最大，占80 %左右，第一激發態對分子體系非線性光學性質起決定作用，因此可借助二能級模型近似計算分子的一階超極化率β。從分子R1到R3，第一激發態的振子強度和躍遷偶極矩逐漸增大，這是由給體的給電子能力的強弱決定的。另外，對于最大吸收波長，理論值和實驗值相差很多，這主要是由CIS方法自身的限制導致，因為它未能考慮電子相關能，過高估計了分子的激發能，從而使吸收波長比實驗值偏小，但是兩者變化的趨勢一致，因此在只需定性比較分子的某些性質時，可以認為這樣的結果是可信的。

比較HOMO和LUMO之間的能隙與激發能發現：HOMO和LUMO之間的能隙越小， 則其激發能也越小。盡管三苯胺給電子能力強于久洛尼啶環，但是因R3中氨基N原子上的兩個苯環發生空間位阻作用破壞了整個分子平面性，阻礙了電子從基態到激發態的躍遷，導致激發能比R2大，最大吸收波長較R2藍移。因此，給體的給電子能力的強弱和分子平面性共同決定激發能大小。

表3 從基態到第一激發態的激發能ΔE(eV)、躍遷偶極矩μeg(Debye)、最大吸收波長λ(nm)、振子強度f及軌道成分

2.5 一階超極化率

本文通過耦合微擾(CPHF)方法以及二能級模型(TEM)計算得到靜態一階超極化率β0和βTEM=，其中Δμeg為基態和激發態之間的偶極矩差， μeg為躍遷偶極矩， ΔE為從基態到激發態的激發能。表4給出了理論計算值，同時列出了在乙腈溶液中分別在1 300 nm和800 nm激發光源下用HRS方法測得的實驗結果[13]。由于采用的從頭計算方法未能充分考慮電子相關效應、基組效應、陰離子效應和溶劑效應等諸多因素的影響，所以計算值與實驗值相差比較大，但兩者表現的趨勢一致，因此在結構類似體系的比較研究中，這些計算值是有效的[3]。

表4 靜態一階超極化率(10-30 esu)和βT0E M(10-30 esu)

表4 靜態一階超極化率(10-30 esu)和βT0E M(10-30 esu)

Δq βCPHF 0 βTEM 0 βExp.0(1300) βExp.0(800)R1 0.211978 159 -87.70 110±7 25±4 R2 0.220272 192 -102.63 220±17 76±5 R3 0.232390 219 -121.72

表4表明了這些靜態一階超極化率與給體的給電子能力之間的關系，雖然βCPHF0與βTEM0值(這里的負值由負的Δμeg引起)相差較大，但是它們都與給體的給電子能力成正比關系如圖3(a)， 3(b)所示。這是因為給體的給電子能力與Δμeg(取絕對值)和μeg成正比關系如圖3(c)， 3(d)所示，從而根據二能級模型可以推得給體的給電子能力與靜態一階超極化率成正比關系。

圖3 給體的給電子能力Δq與βCPHF 0 、βTEM 0 、Δμeg、以及μeg的關系

3 結論

在HF/6-31G(d)水平上研究了吡啶鹽衍生物分子的電子光譜和非線性光學性質。這類D-π-A型衍生物分子具有良好的分子平面骨架，有利于電荷在內傳輸。其中，三苯胺給電子能力最強，久洛尼啶環次之，二甲基苯胺最弱。這些給體的給電子能力與分子內電荷轉移成正比關系。另外，給體的給電子能力還與躍遷偶極矩以及基態和激發態之間的偶極矩差成正比關系，從而使得給體的給電子能力與靜態一階超極化率成正比關系，對于此類分子二能級模型公式適用。盡管三苯胺給電子能力強于久洛定環，但是R3中氨基N原子上兩個苯環由于空間位阻作用而偏離了分子平面，使得電荷轉移能力減弱，因此激發能比R2大，最大吸收波長較R2藍移。同樣， R2的久洛尼啶環通過兩個六元環將給電子基團固定到苯環上，有效地提高了整個分子的平面性，與R1比較，給電子能力大大增強，非線性活性顯著增大。因此，通過對給電子基團空間結構的修飾，可以利用來優化分子的非線性效率。這些簡單關系有助于我們深層次研究結構類似分子的結構與非線性光學性質之間的關系，從而為非線性材料的設計及合成提供理論幫助。

[ 1] Polymeric Materials and their Orientation Techniques for Second-Order Nonlinear Optics[ J] .Advances in Polymer Science，Vol.161.

[ 2] Recent Progress in Second-Order Nonlinear Optical Polymers and Dendrimers[ J] .Progress in Polymer Science， 2008， 33：1013-1058.

[ 3] 逯振平，韓奎，李海鵬， 張文濤， 黃志敏， 沈曉鵬.4-N-甲基苯乙烯砒啶鹽衍生物非線性光學性質的理論研究[ J].原子與分子物理學報.2006， 23(5)：905-910.

[ 4] 吡啶鹽二維電荷轉移分子的設計-合成和超極化率的測定[J].化學學報， 2000， 58(4)：384-389.

[ 5] 李海鵬，韓奎，沈曉鵬，黃志敏， 王群.半花菁衍生物分子第一超極化率頻率色散效應的理論研究[ J] .光學學報， 2005， 25(5)：655-660.

[ 6] 劉頌豪，赫光生.強光光學及其應用[ M] .第一版.廣東：廣東科技出版社， 1995.14-14.

[ 7] Talgat M.Inerbaev， Shigeki Saito， Rodion V.Belosludov.etc.Excited State Properties and Quadratic Optical Nonlinearities in Charged Organic Chromophores：Theoretical Analysis[ J] .The Journal of Chem ical Physics， 2006， 125：234702.

[ 8] 李海鵬，韓奎，逯振平，沈曉鵬，黃志敏， 張文濤，白磊.有機分子第一超極化率色散效應和雙光子共振增強理論研究[ J] .物理學報， 2006， 55(4)：1827-1831.

[ 9] Frisch M J， et al.， Gaussian 03， Revision D.01[ sw] .Gaussian，Inc.， Wallingford CT， 2004.

[ 10] Julia E.Rice， Roger D.Amos， Susan M.Colwell， Nicholas C.Handy， Javier Sanz.Frequency-Dependent Hyperpolarizabilities with Application to Formaldehyde and Methyl Fluoride[ J].J.Chem.Phys， December 1990， 93(12)：8828-8839.

[ 11] 葉成， (法)習斯(Zyss， J).分子非線性光學的理論與實踐[ M] .第一版.北京：化學工業出版社， 1996.94-101.

[ 12] 劉暢，黃維，呂昌貴， 崔一平.吡啶鹽JVPI的合成及雙光子吸收特性[C] //2008年東南大學校慶學術報告會.

[ 13] Benjamin J.Coe a， Simon P.Foxon a， Elizabeth C.etc.The Syntheses， Structures and Nonlinear Optical and Related Properties of Saltswith Julolidinyl Electron Donor Groups[ J].Dyesand Pigments 82(2009)171-186.