基于辛普森面積的多邊形凹凸性識別算法

陳亞婷,嚴泰來,朱德海

(中國農業大學信息與電氣工程學院,北京 100083）

基于辛普森面積的多邊形凹凸性識別算法

陳亞婷,嚴泰來,朱德海

(中國農業大學信息與電氣工程學院,北京 100083）

多邊形頂點的凹凸性是其重要的形狀特征,常被應用于制圖綜合、模式識別等方面。該文利用多邊形特有的面積屬性,將辛普森面積計算公式引入多邊形頂點的凹凸性識別算法中,通過計算多邊形中待判斷頂點與其相鄰兩頂點所構成三角形的辛普森面積與整個多邊形的辛普森面積的符號異同來判斷頂點凹凸性。經推算證明,該算法對于復雜多邊形的頂點凹凸性識別同樣有效。

辛普森面積計算公式;頂點凹凸性;復雜多邊形;多邊形方向

為了詳細了解各種地物的信息,常采用大比例尺進行調查成圖;但在不同領域使用地圖時,對地圖詳細度的要求不一致。例如,在分析一個地區的總體地域特征時,需要大范圍瀏覽地物,以把握整體特性;通常的做法是以大比例尺數據作為數據源,過濾掉冗余信息,保留地物特征,形成概要的小比例尺地圖。在該過程中,對多邊形進行特征提取是最關鍵的步驟。凹凸性是多邊形的重要形狀特征,如能預先確定多邊形的凹凸性,可使問題簡化。

現有的多邊形頂點凹凸性識別法有角度法、叉積法、拓撲映射法以及基于邊向量斜率比較的方法等[1-6]。其中最基本的算法是角度法,但其計算效率低,且易出現奇異值。另一典型算法是叉積法,即在判別多邊形方向的前提下,利用多邊形相鄰3點Pi-1、Pi、Pi+1的坐標組成的行列式值與零的關系來確定 Pi與有向線段 Pi-1Pi+1之間的位置關系,從而得到頂點 Pi的凹凸性。該算法正確率高,但計算量較大,且不適用于復雜多邊形。本文利用多邊形特有的面積屬性,提出了基于辛普森面積的多邊形頂點凹凸性識別算法,利用多邊形3個連續頂點構成三角形的辛普森面積與整個多邊形的辛普森面積符號的異同來識別簡單多邊形的凹凸性。

1 相關定義

(1）簡單多邊形:若多邊形由平面上 n個不同點P1,P2,…,Pn首尾相連構成,且滿足任意兩條不相鄰邊都不相交,任意相鄰的三點都不共線,稱該多邊形為簡單多邊形,其中 P1,P2,…,Pn為其頂點。

(2）復雜多邊形:若一多邊形由多個簡單多邊形組成,且滿足任意兩個簡單多邊形邊界不相交,則稱該多邊形為復雜多邊形,所有組成該復雜多邊形的簡單多邊形的頂點稱為該復雜多邊形頂點。

(3）多邊形的方向:使用辛普森公式計算多邊形面積,若所得辛普森面積為正,則稱該多邊形方向為正方向;否則,稱其方向為負方向。

(4）頂點的凹凸性:對于多邊形某個頂點,若交于該頂點的相鄰兩邊所形成的內角(即該多邊形所圍成有界區域內所形成的角）小于180°,稱該頂點為凸點;若大于180°,稱其為凹點;若等于180°,則稱該頂點不具有凹凸性。

(5）結點:GIS中線的終點、起點和交點稱為結點。

(6）弧段:GIS中兩個結點之間的線段稱為弧段。

2 凹凸性識別算法原理

凹凸性識別算法建立在GIS的圖形存儲數據結構基礎上。基于該數據結構,將辛普森面積計算公式應用于多邊形和待判斷頂點所在三角形,即可判定頂點的凹凸性。

2.1 存儲數據結構[7]

GIS中多邊形的存儲使用多邊形-弧線拓撲結構定義,即數據結構中不直接存儲多邊形頂點坐標信息,而是存儲組成該多邊形的弧段。一個簡單多邊形由一系列組成其邊界的弧線規定,復雜多邊形則由多組弧線構成,其中每組弧線定義一個構成該復雜多邊形的簡單多邊形。

為了定義多邊形間的拓撲鄰接性,每個弧段從起始結點到終止結點方向的左側的多邊形稱為左多邊形,右側的多邊形稱為右多邊形。對于復雜多邊形,在遍歷弧段時要求該多邊形區域是所有組成其弧段的同側多邊形,這就要求構成“洞”的弧段方向與外邊界的弧段方向相反。如圖1所示,多邊形區域同是構成其兩個弧段的右多邊形,“洞”弧段的方向與外邊界弧段的方向相反。

圖1 多邊形弧段方向示意Fig.1 The arc direction of polygon

2.2 辛普森(Simpson）面積公式[7,8]

辛普森面積計算公式的基本思想是:按照多邊形的頂點順序依次求出多邊形所有邊與 X軸或者Y軸組成的梯形面積,然后求其代數和(圖2）。一個由n個頂點組成的多邊形的辛普森面積為:

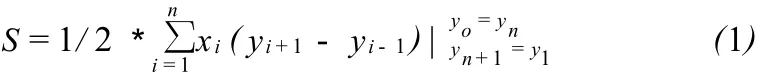
由文獻[8]可知,當多邊形頂點呈順時針方向排列時所得辛普森面積為正值,逆時針方向排列時辛普森面積為負值,而多邊形幾何面積為其辛普森面積的絕對值。

圖2 辛普森面積計算原理示意Fig.2 The illustration of Simpson formula

2.3 基于簡單多邊形的凹凸性識別算法

通過論證可得到如下推理:無論多邊形方向的正負性如何,其頂點與前后兩頂點構成三角形的辛普森面積與多邊形的辛普森面積符號相同時,該頂點必為凸點;反之,則該頂點必為凹點。

推理的證明過程如下:

多邊形 p1p2…pn的辛普森面積為:

當2≤i≤n-1時,三角形 pi-1pipi+1的辛普森面積為:

去除目標頂點 pi后的多邊形 p1 p2…pi-1 pi+1…pn的辛普森面積為:

當i=1或i=n時,令 p0=pn,pn+1=p1,易證上述結論仍成立,即有:

即多邊形 p1p2…pn的幾何面積為多邊形 p1p2…pi-1pi+1…pn與三角形 pi-1pipi+1的幾何面積之和,如圖3a所示,則目標頂點 pi為凸點。

即多邊形 p1p2…pn的幾何面積為多邊形 p1p2…pi-1pi+1…pn與三角形 pi-1pipi+1的幾何面積之差,如圖3b所示,則目標頂點 pi為凹點。

圖3 頂點凹凸性面積原理示意Fig.3 The relationship between convex-concave feature and area

根據該推理,多邊形頂點的凹凸性可通過判斷多邊形與頂點三角形的辛普森面積符號是否一致得出。以簡單多邊形 p1p2…pn為例,令 p0=pn,pn+1=p1。基于辛普森面積的頂點凹凸性識別算法的實現步驟為:1）按照多邊形頂點存儲順序遍歷該多邊形所有頂點,根據辛普森面積公式求出多邊形辛普森面積的兩倍(2S）。2）從起始頂點開始遍歷,獲取目標頂點 pi的坐標值,并獲取其前一頂點 pi-1和后一頂點 pi+1的坐標;利用辛普森面積公式計算三角形 pi-1pipi+1辛普森面積的兩倍(2Si）。3）判斷2S與2Si的符號:若2S與2Si同號,即2S＊2Si＞0,則目標頂點 pi為凸點;若2S與2Si異號,即2S＊2Si＜0,則目標頂點 pi為凹點。4）獲取下一個目標頂點,轉至步驟2。當所有頂點已遍歷結束,退出程序。

在上述過程中,通過判斷多邊形辛普森面積 S的符號得到多邊形的方向。考慮到多邊形的方向對頂點的凹凸性并無影響,因此算法中省略多邊形方向的判斷,直接使用2S與2Si的乘積符號得到頂點的凹凸性。這就避免了由于坐標系不一致(如 X坐標軸與 Y坐標軸換位）或初始多邊形的方向不同帶來的預處理過程,增強了算法的適應性。

2.4 復雜多邊形中算法有效性驗證

區別于現有的典型識別算法,基于辛普森面積的頂點凹凸性識別算法對復雜多邊形同樣有效,其理論驗證過程如下。

首先,將辛普森面積計算公式推廣到復雜多邊形的面積計算中。按照辛普森面積公式的定義,復雜多邊形的辛普森面積應表示為組成多邊形的所有邊界弧段上頂點與 X軸或 Y軸組成的梯形面積的代數和。則圖4中復雜多邊形的辛普森面積為:

由2.1節可知,復雜多邊形中“洞”弧段的存儲方向與外部多邊形的弧段方向相反。因此,“洞”弧段構成的簡單多邊形的辛普森面積與外部簡單多邊形的辛普森面積符號不一致,即有 S(papbpc）×S (p1p2…pn）＜0,則:

即該復雜多邊形的面積為外部多邊形的幾何面積扣除“洞”的幾何面積。因此,辛普森公式對復雜多邊形成立。

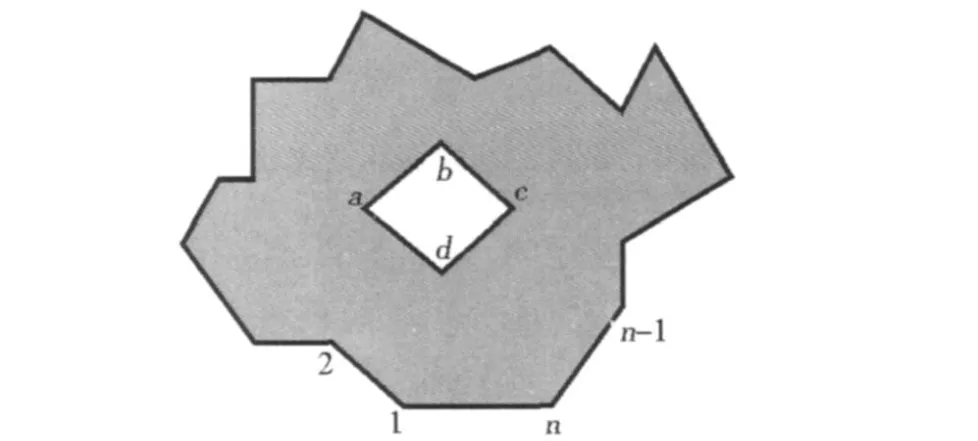
圖4 復雜多邊形辛普森面積示意Fig.4 An example of complex polygon

設一復雜多邊形的辛普森面積為 S,其內部“洞”弧段對應的簡單多邊形的辛普森面積為 S洞。由于復雜多邊形內部的“洞”弧段與外邊界弧段的方向相反,而外邊界弧段的方向決定了該復雜多邊形的辛普森面積正負性,則 S＊S洞＜0。若 Sk為“洞”弧段對應的簡單多邊形上的凸頂點,則 Sk＊S洞＞0。由上面兩式得Sk＊S＜0,即“洞”弧段對應的簡單多邊形的凸頂點為該復雜多邊形的凹頂點。同理可得,“洞”弧段對應的簡單多邊形的凹頂點為該復雜多邊形的凸頂點。

綜上可知,該算法對復雜多邊形的頂點凹凸性識別同樣有效。

3 結語

本文提出了基于辛普森面積的多邊形頂點凹凸性識別算法,利用多邊形中待判斷頂點與其相鄰兩頂點所構成三角形的辛普森面積與整個多邊形的辛普森面積的符號異同來判斷頂點凹凸性,避免了對多邊形自身方向的判斷,從而避免了由于坐標系統不一致(如 X軸、Y軸位置交換）和多邊形方向變化帶來的預處理過程,增強了算法的適應性。該算法時間復雜度為O(n）,計算效率相對較高,可為圖斑化簡、點線空間位置判斷等方面[9,10]的應用提供參考。該算法對復雜多邊形的凹凸性識別同樣有效。

[1] 劉曉平,吳磊.簡單多邊形方向及頂點凹凸性的快速判定[J].工程圖學學報,2005,26(4）:124-129.

[2] 趙軍,張桂梅,曲仕茹.利用極點順序的多邊形頂點凹凸性判別算法[J].工程圖學學報,2007,28(1）:55-59.

[3] FEITO F R,TORRESJ C,URENA A.Orientation,simp licity, and inclusion test for planar polygons[J].Computers&Graphics,1995,19(4）:595-600.

[4] 汪學明.多邊形頂點凸凹性識別算法的研究與實現[J].計算機應用,2005,25(8）:1787-1788.

[5] 龐明勇,盧章平.基于邊向量斜率比較的簡單多邊形頂點凸凹性快速判別算法[J].工程圖學學報,2004(3）:73-77.

[6] 劉潤濤.任意多邊形頂點凸、凹性判別的簡捷算法[J].軟件學報,2002,13(7）:1309-1312.

[7] 朱德海,嚴泰來,楊永俠.土地管理信息系統[M].北京:中國農業大學出版社,2000.

[8] 李建林.面積平衡約束下的土地利用數據綜合方法研究[D].中國農業大學,2008.

[9] 宋曉眉,張曉東,李健林.一種高準確度的約束Delaunay三角網生成算法研究[J].地理與地理信息科學,2009,25(1）:99-102.

[10] 李健林,朱德海,宋曉眉,等.一種基于面積平衡的圖斑化簡算法[J].地理與地理信息科學,2009,25(1）:103-106.

An Algor ithm for Identifying Convex-Concave Vertices of Polygon Based on Simpson Formula

CHEN Ya-ting,YAN Tai-lai,ZHU De-hai
(College of Inform ation and Electrical Engineering,China A griculture University,Beijing 100083,China）

The convex-concave quality of vertices is an important character of polygon,w hich isw ildly used in cartographic generalization,pattern recognition and so on.To identify convex-concave verticesof polygon,an algorithm is p roposed in this paper w hich makes use of Simpson fo rmula.Compared w ith o ther similar algo rithm s,it can identify convex-concave vertices efficiently w ith better app lication adap tability.Furthermo re,it is p roved to be effective in identifying convex-concave vertices of comp lex polygons as well.

Simpson formula;convexity-concavity of vertices;complex polygon;direction of polygon

TP301.6

A

1672-0504(2010）06-0028-03

2010-03-16;

2010-06-01

北京市第二次土地調查技術實施細則編寫項目

陳亞婷(1986-）,女,博士研究生,研究方向為GIS技術在國土資源管理方面的應用。E-mail:comeon_cyt@126.com