倚岸型潮流脊體系中的深槽沖刷——以江蘇如東海岸為例

劉秀娟，高抒，汪亞平

（1．中國地質大學資源學院，湖北 武漢 430074；2．南京大學海岸與海島開發教育部重點實驗室，江蘇 南京 210093）

倚岸型潮流脊體系中的深槽沖刷
——以江蘇如東海岸為例

劉秀娟1，高抒2，汪亞平2

（1．中國地質大學資源學院，湖北 武漢 430074；2．南京大學海岸與海島開發教育部重點實驗室，江蘇 南京 210093）

江蘇如東海岸的潮流脊體系位于南黃海輻射狀沙脊群南部，由沙脊及脊間深槽組成，為“倚岸型”潮流脊體系。本文采用水平一維模型模擬深槽從初始形態沖刷至均衡態的演變過程，用不同的潮差及初始剖面坡度等參數運行該模型，以了解深槽沖刷深度的主要控制因素及其對深槽均衡態的影響。數值實驗結果表明：(1) 給定初始剖面的坡度、潮差等參數，經歷一定時間的沖刷之后剖面達到均衡態，其后剖面形態保持穩定，不隨時間改變；(2) 若僅給定初始剖面的坡度，則潮差越大，達到均衡態時深槽的沖刷深度越大，而且潮差的變化對沖刷深度有顯著影響；(3) 若僅給定潮差，則初始剖面的坡度越大，均衡態時深槽的沖刷深度越小且初始剖面坡度的改變對沖刷深度有顯著影響。

倚岸型潮流沙脊；均衡深度；潮差；數值模擬；江蘇海岸

潮流脊是海岸或大陸架淺海海底特有的地貌形態，形成于沉積物供應充分和潮流較強的環境。潮流脊在世界范圍的陸架區分布廣泛，根據其一端是否和岸線相連可分為“倚岸型”潮流沙脊和“離岸型”潮流沙脊。國外對潮流脊的研究開始于20世紀60年代，Off于1963年提出了潮流脊 (Tidal Current Ridges) 的概念，并首次將潮流脊與水動力條件聯系起來，認為潮流脊是潮流塑造的[1]。之后，學者們對歐洲北海的潮流沙脊進行了研究，探討其水文、泥沙輸運及沙脊形成與維持機制[2-5]。國內從20世紀60年代開始對黃海輻射潮流沙脊群進行研究，如1979－1985年間的江蘇海岸帶資源調查[6]，1990－1995年國家自然科學基金“八五”重點課題“黃海輻射沙洲形成演變研究”等[7]，并形成了一系列觀點，如：潮流運動是潮流脊發育的動力[8-11]；在潮流脊的演變過程中，潮流始終起著主導作用[12]；南黃海沙脊群樞紐地區處于增長、擴張過程，南部區域變化較弱而北部變化強烈并繼續維持原有的脊槽相間的形狀[13]，而劉振夏、夏東興則認為潮流脊的建造力量是縱軸橫向環流[14]。遙感和GIS也被用于輻射沙脊群的穩定性研究[15,16]。對輻射沙脊群脊間水道的懸沙濃度垂線分布及懸沙輸移的動力機制也進行了初步分析[17]。

國內對潮流脊的形成、演變機制及穩定性的分析主要限于對沙脊群區域潮流場和泥沙運移的數值模擬，而對沙脊間深槽穩定性的動力機制研究還較為薄弱。利用脊間深槽建港或作為航道，其穩定性是一個首要問題，因此本文擬對江蘇如東海岸潮流脊體系中的深槽沖刷達到均衡態的演變過程、沖刷深度及主要控制因素進行定量研究，探討各控制因素對深槽沖刷深度的影響。

1 倚岸型潮流脊特征

江蘇如東海岸的潮流脊體系位于南黃海輻射狀沙脊群南部（圖1），是一個典型的“倚岸型”潮流脊體系，即潮流沙脊的一端和海岸相連，由一系列近似垂直于或斜交于岸線的沙脊及脊間深槽組成。該沙脊體系中的深槽長度一般不超過3 km，水深不超過5 m。如東段潮灘寬度為5 km左右，潮灘坡度在0.05 % ～ 0.09 %。該海區為正規半日潮區，平均漲潮歷時6.26 h，平均落潮歷時6.11 h。本區的水動力特征為：潮差較大，最大潮差為8.08 m，最小潮差為1.79 m，平均潮差為4.61 m；潮流為往復流性質，漲潮流主流向為240° ～ 300°，落潮流主流向為70° ～ 100°；海流的近底層流速較大，實測最大值為1.4 m/s，大潮時流速大于0.4 m/s。從懸沙濃度分布看，近岸懸沙濃度極高，最高達1.2 kg/m3，向海方向懸沙濃度逐漸降低。本區底質主要由砂質粉砂和粉砂質砂組成，占研究區面積的70%以上，較粗的粉砂質砂主要集中在深槽部位，而砂質粉砂則主要分布在潮流沙脊頂部①。

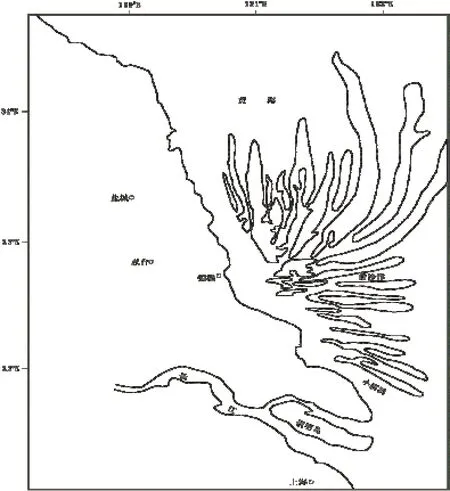
圖 1 研究區概況Fig.1 Study area

2 研究方法

2.1 模型的建立

2.1.1 潮流流速 本文暫不考慮深槽的寬度和沙脊的存在對深槽沖刷的影響，而以一維模型方法模擬深槽水深的變化。如圖2所示，BC為潮間帶，CD為高潮面，BF為低潮面，坐標原點O設在平均海平面與海岸交界處，設平行于深槽走向且向外海的方向為X軸正向，垂直向下為Z軸正向，A(x,z)為潮下帶深槽中的任意一點，則漲潮期間潮間帶納潮量的變化與垂線平均流速的關系為：

①汪亞平，賈建軍，高抒，等.江蘇洋口港沉積動力學條件與海底穩定性 [R].2003.

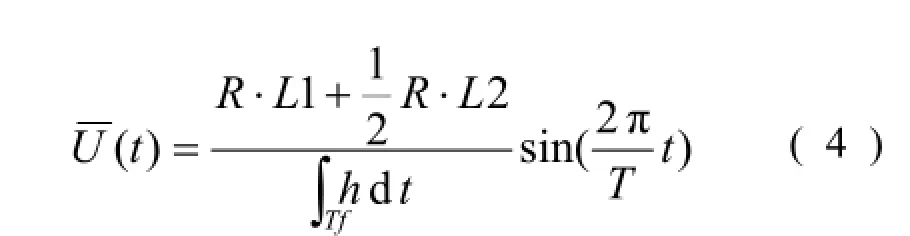
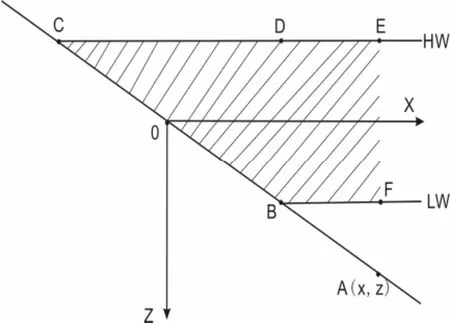
圖 2 海岸剖面上以平均海平面與海岸的交點為原點建立的直角坐標系。A(x, z) 為深槽中任意一點，陰影部分為漲潮期間A點以上潮間帶納潮量的變化量Fig.2 Cartesian coordinate system with the origin being located at the intersection of the mean water level on the coast.A(x, z) denotes a point within the channel, and the sheltered area represents tidal prism for the inter-tidal area above the point A

2.1.2 再懸浮引起的泥沙通量 計算潮周期內再懸浮引起的沖刷通量的公式[18]為：

式中：C100為拖曳系數；u100為距離底床1 m處的流速。該沙脊區靠近海岸，水深較淺，因此在水深范圍內垂向流速分布滿足von Kármán- Prandtl方程：

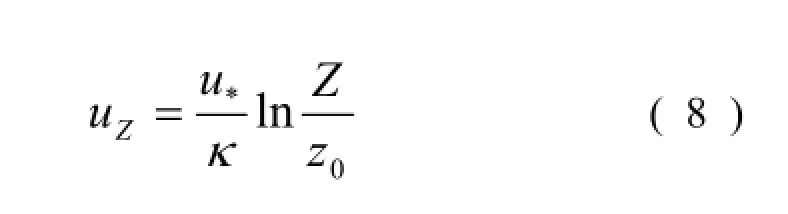
式中：uZ為距床面垂向距離為Z處的流速；u*為摩阻流速；κ為Kármán常數 (=0.4)；z0為粗糙長度。從公式 (8) 可得：

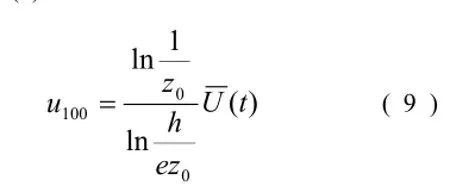
將式 (4) 代入式 (9) 可得海岸形態和水動力之間的關系：

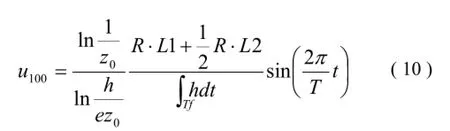
τcr用Shields曲線確定，步驟如下：

(1) 根據實測數據計算出u*或給u*一個經驗值；

(2) 根據海水的溫度和鹽度確定動力粘滯系數υ或直接給出經驗值，從下式求出Re*；

(3) 根據Re*在Shields曲線上確定對應的縱坐標θc，然后根據式 (14) 求出τcr。

式中：ρs為沉積物密度。

2.1.3 底床變形 深槽底床的變形公式為：

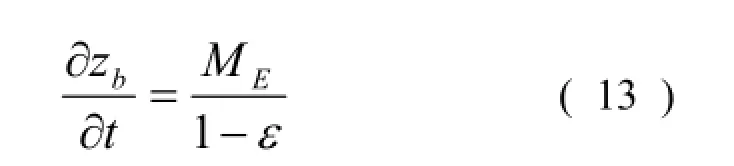
式中：zb表示底床深度；ε表示底床孔隙度。

2.2 模型的運行

2.2.1 沖刷深度計算 如東近岸脊間深槽長度一般不超過3 km，深度一般不超過5 m①。在檢驗這種方法是否能有效模擬深槽演變至均衡態時的沖刷深度時，深槽長度取為3 km，潮周期為12 h 37＇，海水密度ρ取1 026 kg/m3，沉積物密度ρs為2 650 kg/m3，漲潮歷時為6.26 h①，沉積物粒徑D為 3.1×10-5m①，水體運動粘滯系數臨界摩阻流速為3.87×10-2m/s[19]，粗糙長度z0為 1.98×10-2m[19],C100取經驗值3×10-3[20]，判定深槽達到沖淤平衡的極小值?hmin取1.2×10-4m。潮周期內當近底部切應力超過臨界切應力時，則計算底床上因再懸浮引起的沖刷通量。

2.2.2 各控制因素對深槽沖刷深度的影響 在探討潮差和初始剖面的坡度對深槽沖刷深度的影響時，深槽長度仍采用如東近岸潮流深槽通常的長度。為分析潮差對深槽深度的影響，給定初始剖面的坡度，使潮差在2 ～ 6 m范圍內變動；為分析初始剖面的坡度對沖刷深度的影響，給定潮差，使初始剖面的坡度在0.05% ～ 0.1%范圍內變動。各參數取值見表1。

表 1 模型中各參數取值Tab.1 Values of the parameters for the model

3 模擬結果

3.1 深槽的均衡態

將2.2.1 中如東的相關數據輸入模型，計算結果如圖3所示，深槽的剖面形態隨時間而演變，但變化速度隨時間顯著減小，并最終趨近于均衡態，即海底的沖淤處于動態平衡之中，剖面形態不隨時間改變。在圖3中，歷時2.5 a與歷時3 a的剖面形態是重合的，說明歷時2.5 a時剖面形態已穩定，即深槽處于均衡態。深槽均衡態的存在是因為隨著深槽的刷深，流速逐漸降低，水流對泥沙顆粒的切應力也隨之降低，當小于臨界切應力時，水流的切應力不足以起動泥沙顆粒，深槽即處于均衡態。

圖3顯示，當深槽長度不超過3 km時，均衡態時深槽海圖水深不超過5 m，這和如東海岸的“倚岸型”潮流沙脊體系中的深槽深度是吻合的。

3.2 潮差對沖刷深度的影響

當模型的其它輸入參數不變而只改變潮差時，則模型運行結果如圖4所示，當潮差為2 m時，和初始剖面相比，均衡態時的深槽剖面在左端小范圍內有輕微沖刷，其余部分基本沒有變化，整個剖面的平均沖刷深度僅為0.04 m；當潮差為4 m時，深槽的平均沖刷深度為1.63 m；當潮差為6 m時，深槽的平均沖刷深度為2.18 m；當潮差在2 ～ 6 m的范圍內變動時，潮差每增大1 m，深槽沖刷深度增加0.55 m，說明潮差對深槽沖刷深度有顯著影響。這是因為漲潮歷時不變，潮差越大，潮流的流速越大，水流的切應力就越大，從而起動的沉積物顆粒越多，沖刷量也越大。

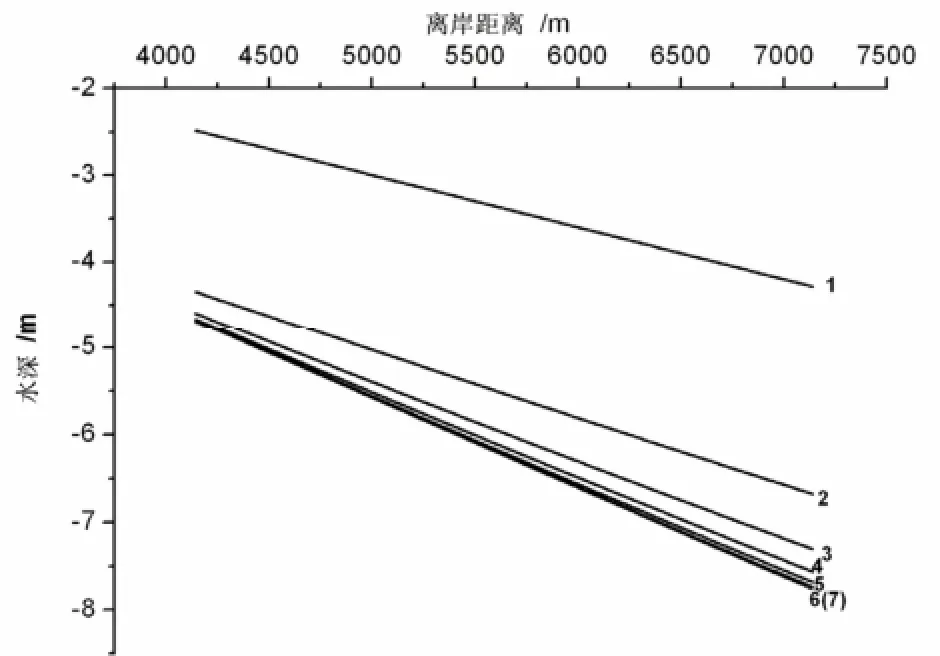
圖 3 模擬的深槽剖面演變過程1：初始剖面形態；2：歷時0.5 a時的剖面形態；3：歷時1.0 a時的剖面形態；4：歷時0.5 a，1.5 a時的剖面形態；5：歷時0.5 a，2.0 a時的剖面形態；6：歷時0.5 a, 2.5 a時的剖面形態；7：歷時3.0 a時的剖面形態Fig.3 Modeled evolution of the channel1.the initial profile of the channel; 2.the profile after six months; 3.the profile after one year; 4.the profile after one year and six months; 5.the profile after two years; 6.the profile after two years and six months; 7.the profile after three years.

3.3 初始剖面的坡度對沖刷深度的影響

當模型的其它輸入參數不變而只改變初始剖面的坡度時，則運行結果如圖5所示，當深槽初始剖面的坡度為0.05%時，均衡態時深槽的平均沖刷深度為4.38 m；當初始剖面的坡度為0.07%時，深槽的平均沖刷深度為2.69 m；當初始剖面的坡度為0.09%時，深槽的平均沖刷深度為1.36 m；當初始剖面的坡度在0.05% ～ 0.09%的范圍內變動時，坡度每增大0.01%，深槽的沖刷深度就減小0.76 m，說明初始剖面的坡度對深槽沖刷深度有顯著影響，這是因為深槽初始剖面的坡度越大，潮流流速越小，從而起動的沉積物顆粒越少，沖刷量也越小。

4 討 論

在潮周期內當近底部切應力超過臨界切應力時，海底會出現沖刷，則需計算底床上因再懸浮引起的沖刷通量；而當近底部切應力小于臨界切應力時，通常底床會出現泥沙落淤。為簡單起見，本文忽略因懸沙落淤而引起的底床堆積。可實際上，當潮周期內近底部切應力小于臨界切應力時，則懸沙落淤會造成底床的變形。因此實際深槽沖刷達到均衡態的歷時要長于本文的計算結果。盡管如此，本項研究表明，底質為細顆粒沉積物的深槽達到均衡態的歷時遠遠短于沙礫質底床的歷時[21]。

雖然江蘇如東海岸潮流流速較大，表層沉積物較細，沉積物的輸運主要以懸移質方式為主，但是本區漲潮歷時略大于落潮歷時，平均漲潮流速小于平均落潮流速，潮周期內推移質有一定的向海凈輸運。本項研究只是初步模擬潮流深槽的沖刷演變，故忽略了推移質輸運引起的沖淤效應。如模擬更接近自然狀態下潮流深槽的沖刷演變則必須考慮潮周期內推移質凈輸運對深槽沖刷的影響。

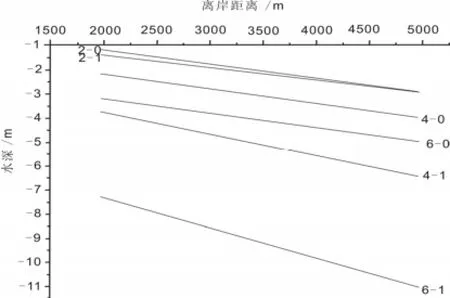
圖 4 不同潮差作用下深槽的沖刷深度2-0：潮差為2 m時的深槽初始剖面；2-1：剖面2-0對應的均衡態剖面；4-0：潮差為4米時的深槽初始剖面；4-1：剖面4-0對應的均衡態剖面；6-0：潮差為6米時的深槽初始剖面；6-1：剖面6-0對應的均衡態剖面Fig.4 Scour depth of the channel with different tidal ranges2-0: the initial profile of the channel with the tidal range of 2m; 2-1: the equilibrium state of the channel corresponding to the profile of 2-0; 4-0: the initial profile of the channel with the tidal range of 4m; 4-1: the equilibrium state of the channel corresponding to the profile of 4-0; 6-0: the initial profile of the channel with the tidal range of 6m; 6-1: the equilibrium state of the channel corresponding to the profile of 6-0

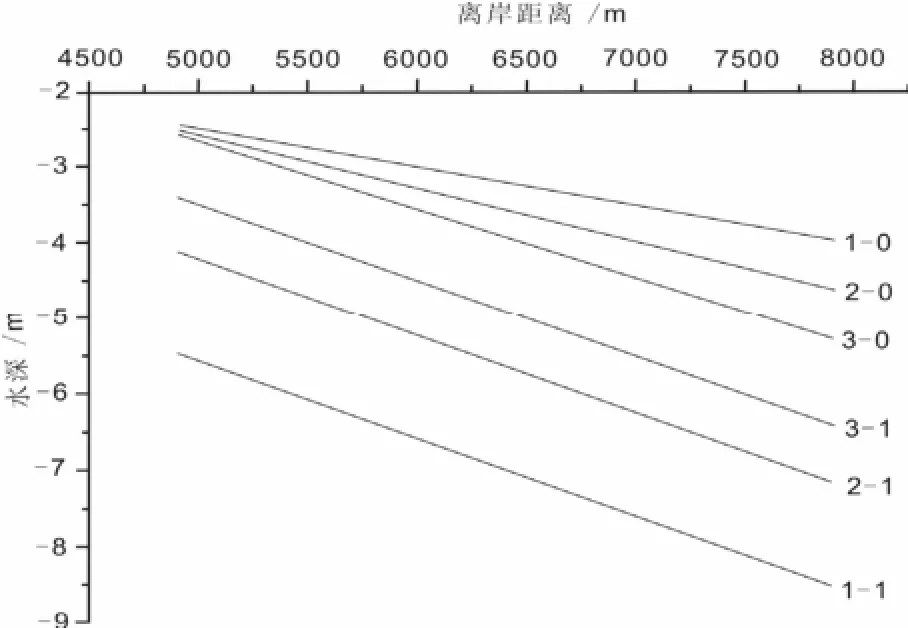
圖 5 不同坡度條件下的深槽沖刷深度1-0：坡度為0.05%時的深槽初始剖面；1-1：剖面1-0對應的均衡態剖面；2-0：坡度為0.07%時的深槽初始剖面；2-1：剖面2-0對應的均衡態剖面；3-0：坡度為0.09%時的深槽初始剖面；3-1：剖面3-0對應的均衡態剖面Fig.5 Scour depth of the channel with different longitudinal seabed slopes1-0: the initial profile of the channel with the obliquity of 0.05%; 1-1: the equilibrium state of the channel corresponding to the profile of 1-0; 2-0: the initial profile of the channel with the obliquity of 0.07%; 2-1: the equilibrium state of the channel corresponding to the profile of 2-0; 3-0: the initial profile of the channel with the obliquity of 0.09%; 3-1: the equilibrium state of the channel associated with the profile 3-0

5 結 論

本文通過模擬江蘇如東海岸“倚岸型”潮流沙脊體系中的深槽沖刷過程中剖面的變化得出如下結論：(1)根據給定初始剖面的坡度、潮差等參數，可以通過一維模擬得出深槽達到均衡態的歷時，如東海岸潮流沙脊體系中的深槽達到均衡態的歷時為2.5 a；(2)若給定初始剖面的坡度，則潮差越大，達到均衡態時深槽的沖刷深度越大且潮差的變化對沖刷深度有顯著影響；(3)若給定潮差，則初始剖面的坡度越大，均衡態時深槽的沖刷深度越小且坡度的變化對深槽沖刷深度有顯著影響。模擬結果表明，深槽在沖刷過程中存在著均衡態，潮差和初始剖面的坡度是深槽沖刷深度的主要控制因素。

[1]Off T.Rhythmic linear sand bodies caused by tidal currents [J].Bulletin of the American Association for Petroleum Geologists, 1963, 47: 324-341.

[2]Huthance J M.On one mechanism forming linear sand banks [J].Estuarine, Coastal and Shelf Science, 1982a, 14: 79-99.

[3]Huthance J M.On the formation of sand banks of finite extent [J].Estuarine, Coastal and Shelf Science, 1982b, 15: 277-299.

[4]Collins M B, Shimwell S J, Gao S, et al.Water and sediment movement in the vicinity of linear sandbank: the Norfolk Banks, southern North Sea [J].Marine Geology, 1995, 123: 125-142.

[5]Williams J J.Offshore sand bank dynamics [J].Journal of Marine Systems, 2000, 24: 153-173.

[6]任美鍔.江蘇省海岸帶和海涂資源綜合調查報告 [M].北京: 海洋出版社, 1986.

[7]王穎.黃海陸架輻射沙脊群 [M].北京: 中國環境科學出版社, 2002.

[8]張東生, 張君倫.黃海海底輻射沙洲區的M2潮波 [J].河海大學學報, 1996, 24(5): 35-40.

[9]張東生, 張君倫, 張長寬, 等.潮流塑造-風暴破壞-潮流恢復—試譯黃海海底輻射沙脊群形成演變的動力機制 [J].中國科學(D輯), 1998, 28(5): 394-402.

[10]王建, 閭國年, 林琿, 等.江蘇岸外潮流沙脊群形成的過程與機制 [J].南京師大學報(自然科學版), 1998, 21(3): 95-108.

[11]諸裕良, 嚴以新, 薛鴻超.南黃海輻射沙洲形成發育水動力機制研究---I.潮流運動平面特征 [J].中國科學(D輯), 1998, 28(5): 403-410.

[12]湯毓祥, 劉振夏, 姚蘭芳.渤海M2潮流及其與遼東淺灘潮流脊發育的關系 [J].海洋通報, 1994, 13(1): 25-30.

[13]李海宇, 王穎.GIS與遙感支持下的南黃海輻射沙脊群現代演變趨勢分析 [J].海洋科學, 2002, 26(9): 61-65.

[14]劉振夏, 夏東興.潮流沙脊的水力學問題探討 [J].黃渤海海洋, 1995, 13(4): 23-29.

[15]陳君, 王義剛, 張忍順, 等.江蘇岸外輻射沙脊群東沙穩定性研究 [J].海洋工程, 2007, 25(1): 105-113.

[16]朱大奎, 龔文平.江蘇岸外海底沙脊群西洋深槽的穩定性分析[J].海洋通報, 1994, 13(5), 36-43.

[17]吳德安, 張忍順.江蘇輻射沙洲陳家塢懸沙變化過程及垂線分布資料分析 [J].泥沙研究, 2007(2): 42-48.

[18]Partheniades E.Erosion and deposition of cohesive soil [J].Journal of the Hydraulics Division,1965, ASCE, 91(HY1): 105-139.

[19]Wang Y P, Gao S, Ke X K.Observations of boundary layer parameters and suspended sediment transport over the intertidal flats of northern Jiangsu, China [J].Acta Oceanologica Sinica, 2004, 23(3): 437-448.

[20]Dyer K R.Coastal and estuarine sediment dynamics [M].Chichester: John Wiley, 1986: 342.

[21]Xie D F, Gao S, Wang Y P.Morphodynamic modelling of open-sea tidal channels eroded into a sandy seabed [J].Geo-Marine Letters, 2008, 28(4): 255-263.

Modeling channel scour associated with shore-attached tidal ridges: A case study from Rudong coast, Jiangsu Province

LIU Xiu-juan1, GAO Shu2, WANG Ya-ping2

(1.Faculty of Earth Resources, China University of Geosciences, Wuhan 430074, China；2.Key Laboratory for Coast and Island Development of the Ministry of Education, Nanjing University, Nanjing 210093, China)

The tidal ridges off the Rudong coast, Jiangsu Province, are a part of the radial tidal ridge system of the southern Yellow Sea.These ridges and the inter-ridge channels represent a kind of shore-attached tidal ridge systems.In this contribution, the evolution from an initial profile to morphodynamic equilibrium was simulated with a horizontal 1-D model.Numerical experiments were carried out for different tidal ranges and longitudinal bed slopes, to evaluate their influence on the equilibrium state of the channel morphology.The results show that: (1) The channel will reach equilibrium during a certain period of time, if the initial profile of the channel and tidal range are known; (2) with an invariable initial profile of the channel, as the tidal range increases, the equilibrium scour depth of the channel also increases, indicating that tidal range has a significant influence on the scour depth; (3) with an invariable tidal range, as the longitudinal bed slope of the channel increases, the scour depth decreases, indicating that the bed slope also affects the final equilibrium state.

shore-attached tidal ridges; equilibrium depth; tidal range; numerical modeling; Jiangsu coast (China)

P737.1

A

1001-6932(2010)03-0271-06

2008-12-05；

2009-11-02

國家自然科學基金項目(No.40876045, 40576040); 國土資源部海洋油氣資源與環境地質重點實驗室開放基金項目(MRE200906)

劉秀娟 (1972－), 女, 副教授, 研究方向為海岸沉積動力學。電子郵箱：xjliu@cug.edu.cn