風扇磨煤機在燃燒褐煤鍋爐中的應用分析
曹 陽,魏 來,張向群,房國成,劉永赤
(1.遼寧東科電力有限公司,遼寧 沈陽 110179;2.國網遼寧省電力有限公司電力科學研究院,遼寧 沈陽 110006)
印尼褐煤的水分和揮發分含量較高,全水分含量高達40%~61%,空 干 基 水 分 為 17%左右,揮 發 分 為50%~60%[1];其灰分和固定碳含量較低,熱值不高,屬于低硫低氮煤[2]。根據《電站磨煤機及制粉系統選型導則》,大型褐煤鍋爐制粉系統一般都采用中速磨煤機或風扇磨煤機制粉系統,但中速磨煤機受熱風溫度、通風能力以及允許溫度等制約條件不適用于全水分Mf>30%的煤種[3];而風扇磨煤機制粉系統可采用高溫爐煙、熱風和冷爐煙或冷風作為干燥介質,可保證高水分煤質滿足鍋爐燃燒要求。同時通過冷煙氣可以控制三介質干燥劑內O2和CO2容積百分比,保證制粉系統運行安全。
1 風扇磨煤機制粉系統特性
1.1 風扇磨煤機制粉系統概況
1.1.1 三介質干燥劑及其冷卻系統
制粉系統采用高溫爐煙、熱風和冷爐煙3種干燥劑,熱風來源于熱二次風,高溫爐煙由爐膛上部抽取,冷爐煙來源于引風機后煙氣,3種干燥劑混合后進入磨煤機。高爐煙冷卻系統采用膜式內冷高溫爐煙管道,通過冷卻水與煙氣逆向流動保護高溫爐煙管道,避免超溫危險。
1.1.2 風扇磨煤機
風扇磨煤機是燃用褐煤鍋爐機組直吹式制粉系統的主體設備,可同時完成煤的磨碎、干燥和輸送三大功能。風扇磨煤機主要由帶護板的機殼和在機殼中高速旋轉的打擊輪組成。機殼上部安裝箱式慣性分離器,在分離器上部裝有風量調節擋板,可改變磨煤機通風量,內部安裝有可調整煤粉細度和磨煤機內部壓力的內、外循環擋板。打擊輪懸臂安裝在雙列軸承支撐的主軸上,主電機經聯軸器直接驅動打擊輪高速旋轉。所用風扇磨煤機的主要參數如表1所示。
1.2 風扇磨煤機制粉系統特點
1.2.1 干燥能力
風扇磨煤機制粉系統適用于高水分褐煤,入口溫度可達550 ℃以上,并可使一次風率達20%~25%,煤粉水分為6%左右,保證鍋爐燃燒要求[4]。理論計算和實際運行經驗均表明,風扇磨煤機的干燥能力比中速磨煤機強很多,對全水分高達60%左右的印尼褐煤干燥效果更為明顯。
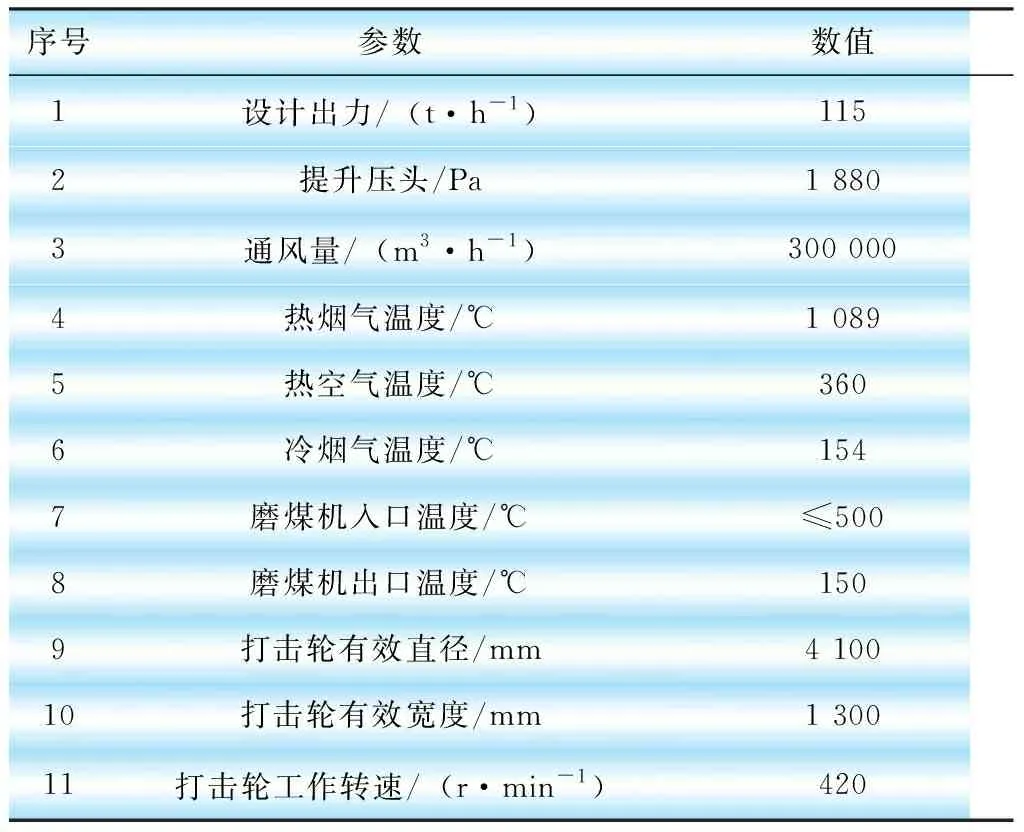
表1 風扇磨煤機主要參數
1.2.2 防爆特性
風扇磨煤機制粉系統采用三介質干燥劑,CO2≥4%,O2<12%[5]。實際運行中,調整冷煙和熱風擋板開度可控制風扇磨煤機入口氧量僅為4%~7%,降低了磨煤機爆炸的可能性,也簡化制粉系統的防爆設計,風扇磨煤機的防爆特性非常適用于高揮發分的印尼褐煤。
1.2.3 對鍋爐爐膛結渣和磨損的影響
風扇磨煤機制粉系統由于一次風中含有大量冷爐煙,可有效降低燃燒器出口燃燒溫度,降低爐膛結渣的可能性。風扇磨煤機磨制出的煤粉較粗,在磨制褐煤時,R90一般要求小于 45%,但褐煤的揮發分較高,粗煤粉并不影響其著火和燃盡,選用較高的R90,可以延長磨煤機耐磨件的使用壽命[6]。
1.2.4 跟蹤機組負荷特性
風扇磨煤機制粉系統可以很好跟蹤機組負荷快速變化,單臺風扇磨煤機瞬時煤量變化為10~50 t,機組平均降負荷速率為18.95 MW/min,平均升負荷速率為19.26 MW/min;緊急情況下,可以在短時間內啟動,無需暖磨,因此風扇磨煤機可以在煤質變化較大和燃燒狀況不好的情況下很好跟蹤負荷變化燃料量。
1.2.5 系統布置特點及維修管理
風扇磨煤機本體占地面積大,其干燥要求需抽取800~1 150 ℃的爐煙,為不影響爐膛熱負荷分布,爐煙由爐膛上部抽出,因抽高溫爐煙管道較粗,不易布置,故將磨煤機盡量布置在爐膛四周。風扇磨煤機維護工作量較大,易磨損件使用壽命在2 000 h,檢修工作較為頻繁。
1.2.6 三介質干燥劑系統
a. 采用三介質干燥劑,可以保持熱風量不變,調節冷煙氣量來適應磨煤機不同運行工況時的干燥要求,摻入冷煙氣可以控制磨煤機入口氧量。
b. 在機組調試期間,三介質干燥劑系統可以靈活控制磨煤機出口溫度,保證運行可靠;在變工況和低負荷運行時,一次風率變化不大,保證燃燒穩定。
c. 能降低燃燒區域溫度水平,減少或避免爐膛結焦,降低NOx的生成。
d. 膜式高溫爐煙管道冷卻系統經常發生漏水現象,而且系統設計較為復雜,初期投資較大。
2 調試運行中遇到的問題及解決方法
2.1 風扇磨煤機軸承溫度超溫跳閘
磨煤機軸承溫度的跳閘保護定值為80 ℃,空載試轉的過程中,試轉45 min左右,軸承溫度就會急速升高并跳閘。后期通過改裝冷油器和冷卻水閥門使冷卻水量達到123 L/min,高于設計要求的100 L/min,嚴格控制冷卻水溫度小于30 ℃,確保冷卻效果;同時改裝了軸承油站的供回油管路,加強了潤滑油的流通性,使軸承超溫問題得以解決。
2.2 風扇磨煤機電機軸承超溫跳閘
磨煤機電機軸承溫度的跳閘保護定值為90 ℃,空載試轉過程中,電機軸承溫度頻繁超溫并跳閘。檢查后發現電機安裝位置出現偏差,造成對輪間隙過大,通過改變對輪間隙以及更換聯軸器使問題得以解決。
2.3 風扇磨煤機出入口溫度控制困難
在磨煤機啟動初期或在低負荷情況下運行時,磨煤機的出口溫度經常超溫。在啟動初期是因為磨煤機啟動時,相比干燥劑的進入速度,煤進入磨煤機有滯后性,易出現超溫現象。針對這一問題,通過減小磨煤機出口擋板開度、打開內外循環擋板,減少出口通流量,同時加快給煤機轉速,使煤盡快進入磨煤機,從而控制住出口溫度。對于低負荷運行情況下磨煤機出口超溫,通過控制冷煙擋板開度以及調整磨煤機給煤量偏置值來控制溫度。
磨煤機在大負荷運行工況下入口超溫原因是在大負荷運行情況下,單臺磨煤機煤量較大,出口溫度相對較低,冷煙擋板開度逐漸減小以保證出口溫度,但由于冷煙量在三介質干燥劑中占比減少,干燥劑溫度提高,造成入口溫度超溫。通過減小磨煤機出口溫度自動調節定值、調整磨煤機給煤量偏置值將煤量減少、適當增加熱風擋板開度等方法來控制磨煤機入口溫度。
2.4 磨煤機支路送粉管道有積粉現象
為保證鍋爐的燃燒,將磨煤機5根支路送粉管道的出口擋板逐層關小,使燃燒呈正三角燃燒方式,減小了上層粉管通風量,導致上層支路粉管發生堵塞現象,尤其在停磨煤機過程中,由于褐煤的揮發分特性極易著火燃燒,存在設備安全隱患。
一次風速、風率過小是造成堵管的主要原因,為防止一次風堵管,運行時要保證一次風速和風量,各燃燒器一次風速設計為22 m/s左右,而且停磨煤機時要將磨煤機內的煤粉全部吹入爐膛后再將磨煤機停止,確保積粉吹掃干凈[7]。
2.5 給煤系統堵塞
3臺機組均出現給煤機漏煤堵塞現象,將給煤機內部堵滿,清理過程復雜耗時,影響機組穩定運行。給煤機堵塞主要是因為中心給料機瞬時落煤量較大,皮帶運量不足,且皮帶寬度有限,導致多余的煤從皮帶兩側掉入給煤機下部,掉入煤量大于清掃鏈的清理速度,最終將給煤機堵死。經分析后,在漏煤口給煤機皮帶兩側加裝了2 m長的整形板,減少了皮帶漏煤量;同時加快清掃鏈的清掃速度,防止漏煤堆積,給煤機堵塞問題得以解決。
3 風扇磨煤機制粉系統的特殊控制
3.1 調門擋板控制
控制磨煤機調門擋板進而調整風扇磨煤機的出口溫度和內部氧量,擋板自動跟蹤出力改變相應開度,其中包括冷煙擋板、熱風擋板、出口分離器擋板和內外循環擋板;冷煙擋板控制出入口溫度,熱風擋板控制內部氧量,出口分離器擋板控制出口通流量,內外循環擋板控制內部壓力。
調整冷煙擋板是控制風扇磨煤機出入口溫度的主要方法,冷煙擋板的自動控制根據2個條件,一是磨煤機出力情況,二是設定溫度與實際溫度的溫度差來開關擋板。隨著磨煤機煤量的不斷增加,出口溫度會不斷下降,冷煙擋板開度逐漸減小,但由于煤量變化對溫度變化影響有滯后性,所以煤量變化的同時給冷煙擋板一個前饋指令。在磨煤機出力穩定后,調整冷煙擋板開度來使實際的出口溫度接近設定值。冷煙擋板開度不小于15%用于控制三介質干燥劑的溫度,防止入口超溫。
磨煤機內部氧含量過高很容易發生爆燃現象,對設備和人身安全都有一定危害[8],尤其是燃用揮發分較高的印尼褐煤,但氧量過低會影響燃燒器出口燃燒,所以控制好氧量非常重要。通過調整熱風擋板來控制內部氧含量。在磨煤機內氧含量低于4%時,熱風擋板全開,而當氧含量高于7%時,熱風擋板全關,在實際運行中將氧含量控制在4.3%~6.5%。
出口分離器擋板調整風扇磨煤機出口通流量,通流量過小會造成管道積粉,而通流量過大磨煤機出口溫度高。綜合考慮后,當磨煤機出力小于50 t/h時,出口分離器擋板保持50%開度,隨著磨煤機出力加大,擋板開度隨之增加,當磨煤機出力為110 t/h時,擋板全開。
磨煤機啟動時防止磨煤機內部超溫超壓,手動開啟內、外循環擋板,而正常運行時內、外循環擋板全關。
3.2 安全防爆控制
鍋爐燃燒高揮發分印尼褐煤需考慮煤場存儲、裝卸、制粉、燃燒以及鍋爐本體可能出現的問題,特別是制粉系統的爆炸將直接導致設備損壞和人員傷害[9]。其中煤粉粗細、磨煤機內部氧含量、風粉混合物溫度和煤粉沉積量是誘發爆炸的決定因素[10]。為了防止制粉系統爆炸,采取了如下措施。
a. 控制煤粉粗細。煤粉越細,其周圍所吸附的空氣或氧氣越多,越容易發生自燃,而當煤粉顆粒大于0.1 mm時幾乎不會發生自燃,風扇磨煤機可以防止煤粉磨制過細。
b. 控制磨煤機內部氧含量。磨煤機內部含氧比例越大,爆炸的可能性也隨之增加,當氧含量小于15%時,爆炸的可能性將大大減小。風扇磨煤機系統選用三介質干燥劑,內部氧含量控制在4%~7%。
c. 控制風粉混合物溫度。風粉混合物溫度越高,煤粉顆粒所需的著火熱越小,燃燒速度越快,越容易發生爆炸,而低于一定溫度則沒有爆炸危險。控制三介質干燥劑中的冷風比例,保證混合物溫度在安全的范圍內。
d. 防止煤粉沉積。煤粉出現沉積后,會在氧氣的作用下發生緩慢氧化形成自燃,造成爆炸。分離器擋板開度不小于50%,有效保證磨煤機出口通流量,進而確保送粉速度大于22 m/s,防止煤粉沉積。
e. 設置防爆門。制粉系統爆炸是由內部壓力過高無處釋放所造成。每臺風扇磨煤機出口處安裝了5個防爆門,其作用就是在磨煤機內部壓力達到爆炸極限值之前提前動作釋放內部壓力,防止爆炸發生。
4 結束語
風扇磨煤機制粉系統以及配備的三介質干燥劑系統具有較強的干燥能力和防爆特性,適用于含有較高水分和揮發分的印尼煤,并且在機組運行過程中能很好跟蹤負荷變化,但其系統占地龐大,且檢修工作量較大。對于風扇磨煤機制粉系統在調試過程中出現的問題都已得到了處理和解決,運行過程中通過相應的自動控制減少了大量的運行操作,并且保證了系統運行的穩定性,滿足了機組長期穩定運行的要求。

