海上定向氣井臨界流量預測方法
于繼飛,管虹翔,顧純巍,齊 桃,李偉超
(1.中海油研究總院,北京 100027;2.中海油(中國)有限公司湛江分公司,廣東 湛江 524057)
海上定向氣井臨界流量預測方法
于繼飛1,管虹翔1,顧純巍2,齊 桃1,李偉超1
(1.中海油研究總院,北京 100027;2.中海油(中國)有限公司湛江分公司,廣東 湛江 524057)
目前廣泛應用的天然氣井臨界流量計算模型均建立在直井基礎之上,沒考慮井斜角對氣體攜液的影響,但海上天然氣井大多為定向井和水平井,現有模型不能準確預測海上氣井是否積液。研究認為,液滴在斜井運動過程中會與管壁發生碰撞,碰撞后液滴呈“半球形”,并最終沿管壁滑動。同時根據海上天然氣井的特點,以Turner模型為基礎,考慮井斜角的影響,對Turner模型進行了修正,提出了海上氣井攜液臨界流量預測的模型,并推導出了快速修正系數。
天然氣;大斜度井;攜液臨界流量;修正系數
1 研究意義
氣井一旦產水,若沒有足夠的能量將水連續帶出井筒,最終在井底會形成積液將氣井壓死,因此避免氣井積液發生的關鍵是保證天然氣有足夠的速度將地層產生的游離水或天然氣中產生的凝析液攜帶到地面[1]。海上氣田往往采用定向井甚至水平井進行開發,一旦發生積液現象造成氣井停產,修井成本極高,對產量影響非常大。因此,在氣藏開發的前期研究設計階段,確定合理的氣藏配產非常重要,對于已經投產的氣井來講,根據氣井的攜液能力判斷什么時間采取合理的措施避免氣井積液也是至關重要的[2]。
目前國內外攜液模型均以直井為研究對象,忽略了定向井井斜對排液的影響[3-4],楊文明在傳統氣井攜液模型的基礎上考慮了井斜角對液滴受力的影響[5],但其假設前提仍然為液滴沿井筒運動,與油管管壁不發生碰撞,這在定向井的實際生產過程中是不合理的。為便于科學地指導生產,建立了海上氣井攜液臨界流量預測模型。
2 臨界速度和臨界流量模型
2.1 液滴在油管內的運動過程
液滴在油管內的受力如圖1所示,在運動過程中液滴主要受到3個力:天然氣對其施加的拽力F、浮力Fr與重力Fg。在直井中拽力與浮力共同作用克服液滴的重力使液滴沿井筒方向前進。但在定向井中,由于拽力沿井筒方向,與浮力、重力的方向存在夾角,這3個力無法使液滴保持平衡,平衡被打破瞬間液滴不是沿井筒方向移動,而是向油管管壁運動,直至貼近管壁發生滑動。
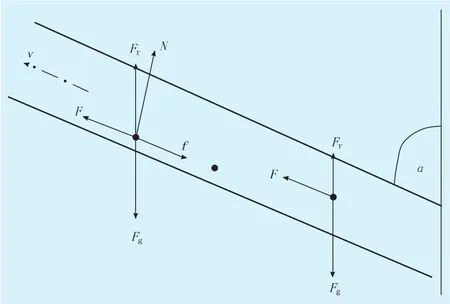
圖1 油管內液滴運動過程
2.2 模型的建立
從圖1可以看出,當液滴與油管管壁接觸后,由于球形液滴受各個方向氣體的壓力(管壁方向除外),使得液滴無法保持1個完整的球形,而是液滴緊緊貼在油管管壁上,保持著近似“半球形”的形狀[6]。此時液滴將受到天然氣對其施加的拽力、浮力、重力、管壁的支撐力N和管壁的摩擦力f。當達到臨界狀態時,液滴前進的動力與阻力達到平衡,即:
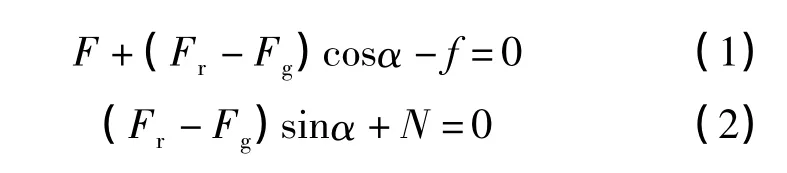

式中:uc為氣井臨界流速,m/s;V為液滴體積,m3;ρl、ρg分別為液體和氣體密度,kg/m3;S 為液滴的垂直投影面積,m2;CD為拽力系數[7-8],為雷諾數的函數,球型牛頓流體(1 000<Re<200 000)取0.44[9]。
Turner認為只要氣井中最大直徑的液滴不滑落,氣井積液就不會發生。液體的最大直徑由韋伯數決定[10],當韋伯數超過30后,氣流的慣性力和液滴表面張力間的平衡被打破,液滴會破碎。因此最大液滴直徑由下面表達式決定:
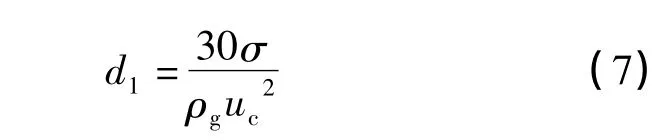
式中:σ為氣液表面張力,N/m。
液滴所受油管管壁摩擦力遵循牛頓內摩擦定律,在管壁處流體擁有最大切應力為:
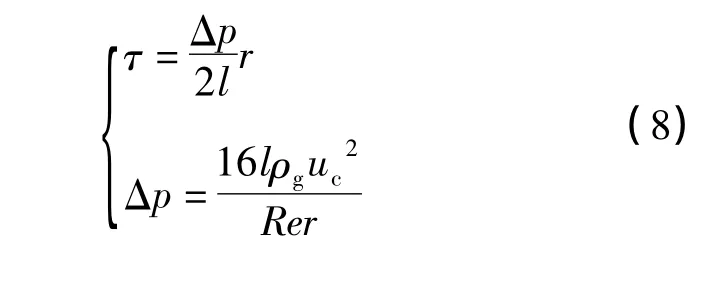
式中:τ為管壁處流體切應力,Pa;Δp為液體流經長度為l的管道壓力損失,Pa;r為管道半徑,m;Re為液體雷諾數。
將公式(8)化簡,可得管壁處液體最大切應力,則液滴所受摩擦力為:

將公式(3)、(4)、(5)、(6)、(9)代入公式(1)可得攜帶最大液滴的最小氣體流速為:

其中,C為修正系數,括號內為Turner公式計算結果。
2.3 井斜角與修正系數
從式(12)可以看出,修正系數由井斜角、拽力系數與雷諾數決定。表1為雷諾數與井斜角對修正系數的影響。可以看出,雷諾數對修正系數影響不大,隨著井斜的增加,修正系數逐漸減小,與之相對應的攜液臨界流速與流量也相應降低,氣井的攜液能力隨之增強。
3 應用實例
以海上某油田的S井為例:S井井斜角為60°,2010年因積液問題關井,通過分析現場的生產數據,發生積液時的臨界產氣量為10×104m3/d。表2為臨界流量計算對比結果。其中,應用Turner模型模擬計算出的結果為13×104m3/d,李閔模型計算結果為5.9×104m3/d,而應用本文方法計算的結果為10.8×104m3/d。可見,應用本文方法計算結果更為接近實際,可以較好的指導生產。
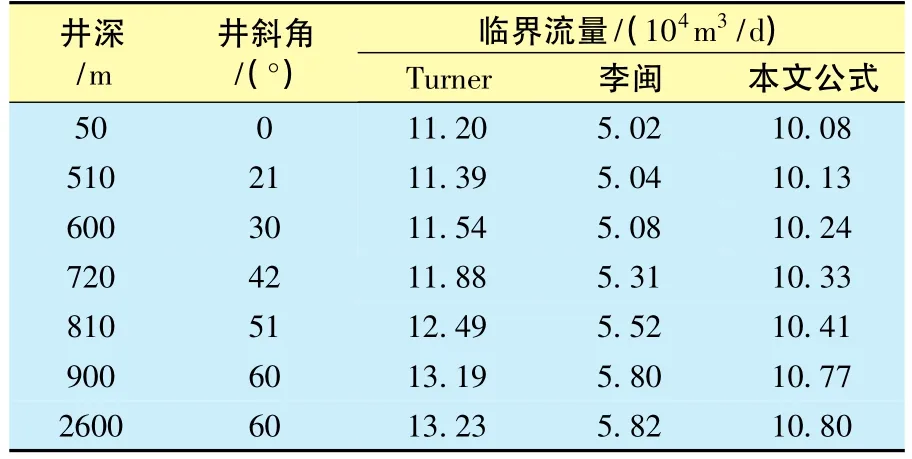
表2 臨界流量計算結果對比
4 結論
(1)針對定向氣井的特點,分析了液滴在斜井中的受力情況,認為液滴最終呈“半球形”沿井壁滑動。
(2)考慮井斜角的影響,對Turner模型進行了修正,并給出了井斜修正系數的速查表,實際使用過程中可以根據本文提供的速查表進行快速修正。
[1]劉廣峰,何順利,顧岱鴻.氣井連續攜液臨界產量的計算方法[J].天然氣工業,2006,26(10):114-116.
[2]康成瑞,徐斌,李興.天然氣井井筒積液預測方法解析[J].新疆石油天然氣,2009,5(2):74 -76.
[3]李閩,郭平,譚廣天.氣井攜液新觀點[J].石油勘探與開發,2001,28(5):105 -106.
[4]李閩,郭平,張茂林,等.氣井連續攜液模型比較研究[J].西南石油學院學報,2002,24(4):30-32.
[5]楊文明,王明,陳亮,等.定向氣井連續攜液臨界產量預測模型[J].天然氣工業,2009,29(5):82-84.
[6]王毅忠,劉慶文.計算氣井最小攜液臨界流量的新方法[J].大慶石油地質與開發,2007,26(6):82-84.
[7]姚玉英.化工原理[M].天津:天津大學出版社,1999:139-141.
[8]魏納,孟英峰,李悅欽,等.天然氣井連續攜液液滴曳力系數研究[J].天然氣技術,2007,1(6):51-52.
[9]向耀權,辛松,何信海,等.氣井臨界攜液流量計算模型的方法綜述[J].中國石油和化工,2009,16(9):55-58.
[10]李士倫.天然氣工程[M].北京:石油工業出版社,2000:253-263.
Prediction of critical flow rate for offshore directional gas wells
YU Ji- fei1,GUAN Hong - xiang1,GU Chun– wei2,QI Tao1,LI Wei- chao1
(1.CNOOC Research Institute,Beijing 100027,China;2.Zhanjiang Branch of CNOOC Ltd,Zhanjiang,Guangdong 524057,China)
The existing models for calculating critical flow rate of natural gas wells were based on vertical wells without considering the effects of deviation angles on gas carrying fluids and they could not accurately predict whether liquid loading exists in offshore gas wells because these wells are mostly directional or horizontal wells.The study results indicate that fluid drops will collide with the tubing wall during the movement and slide along the tubing wall in the shape of“semisphere”after the collision in deviated wells.Based on the characteristics of offshore gas wells and the Turner model and considering the effects of deviation angles,the Turner model was modified to a new model for predicting the critical flow rate of offshore natural gas wells carrying fluids and the quick modification coefficients were derived.
natural gas;highly deviated well;liquid carrying critical flow rate;correction factor
TE319
A
1006-6535(2011)06-0117-03
20110418;改回日期20110920
國家重大專項“南海深水油氣勘探開發示范工程”的部分研究成果(2008ZX05056-002)
于繼飛(1982-),男,工程師,2007年畢業于中國石油大學(北京)油氣田開發工程專業,現從事油氣田開發方面的生產科研工作。
編輯 王 昱

