一個涉及無理式的不等式

羅 釗,王挽瀾,姚 勇

(1.成都大學圖書館,四川成都 610106;2.成都大學信息科學與技術學院,四川成都 610106; 3.中國科學院成都計算機應用研究所,四川成都 610041)

我們在文獻[1]中發現一個頗為有趣的命題及其證明:

命題 如果 ai≥0,i=1,2,…,n,則,

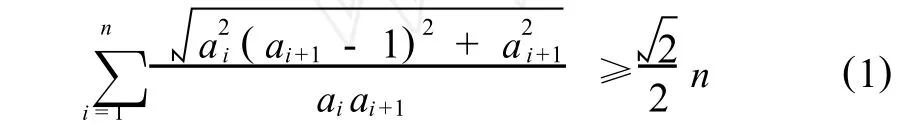
這里,an+1= a1.

在文獻[2]中,我們將其作為例子引用.然而,當本文第二作者擬給出另一證明時,發現若想小改動而保留證明,則應修改條件ai≥0為ai≥1.當拙見通知一些朋友時,我們之間展開了一番有效的研討.其結論是,就盡可能完美而言,宜于進而考究等式條件并將論證修補如下.

定理1 如果 ai＞0,i=1,…,n,那么不等式(1)成立,等式條件為,ai+1+ai= ai+1ai,ai≥1,i =1,…,n.

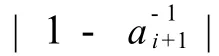
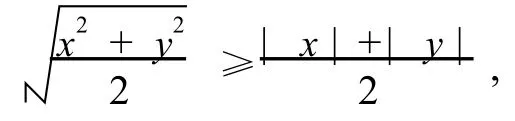
可得,

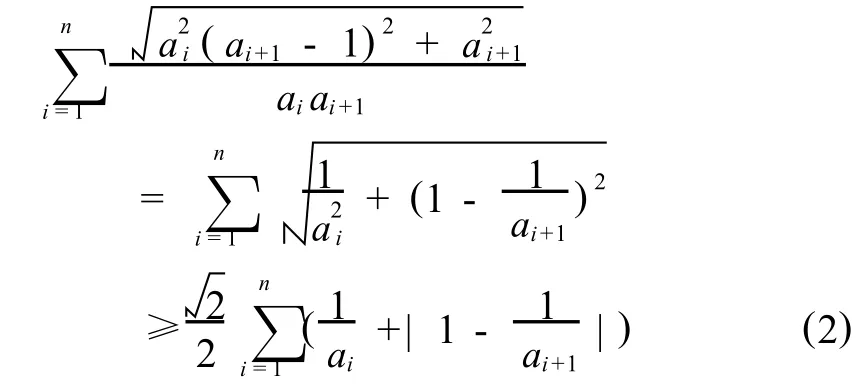
情況1 當 ai≥1時,則,

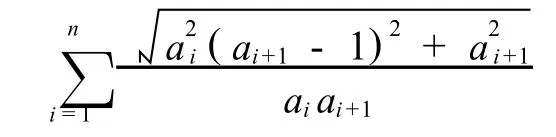
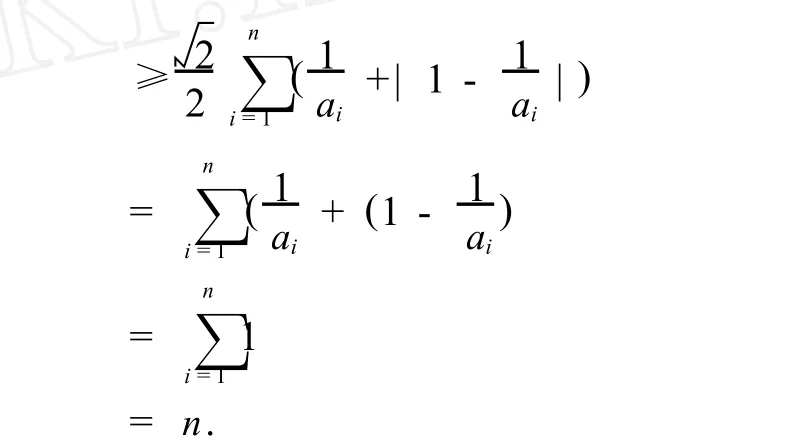
情況2 當0＜ai＜1時,即a-i1＞1,也即2a-i1＞2,則,

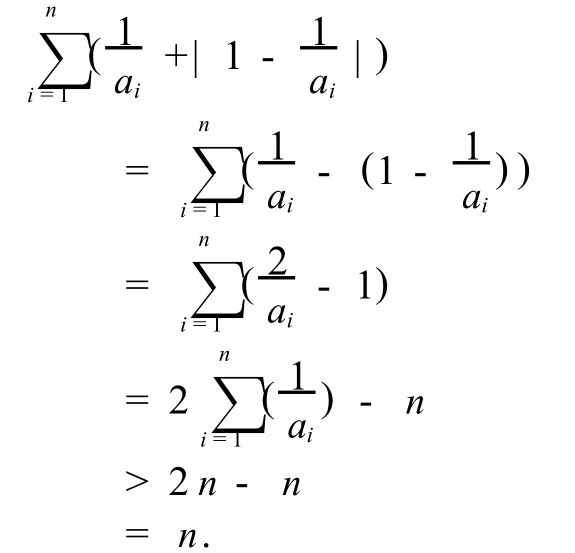
基于上面兩種情況的考究,不等式(1)成立.

第二證明 為了清楚與方便,我們依然將其分為兩種情況論述.

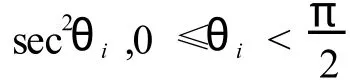
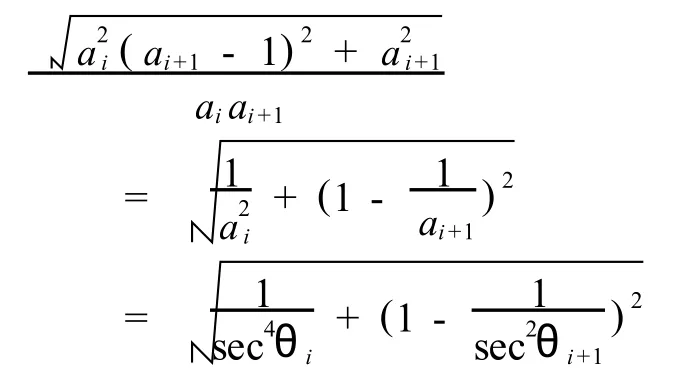
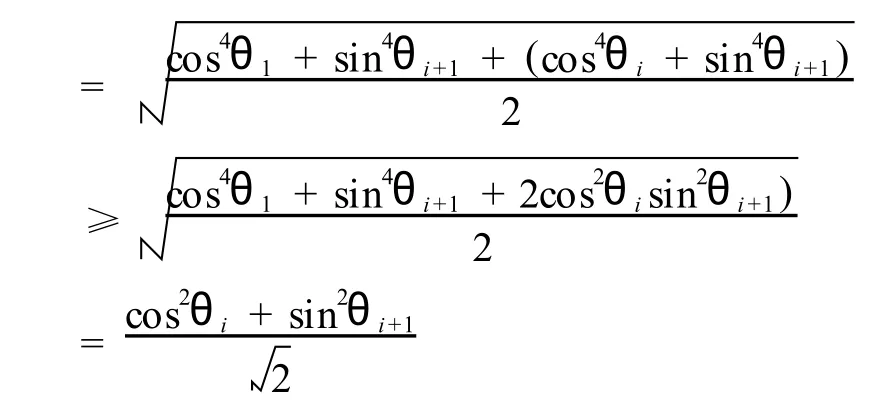
所以,

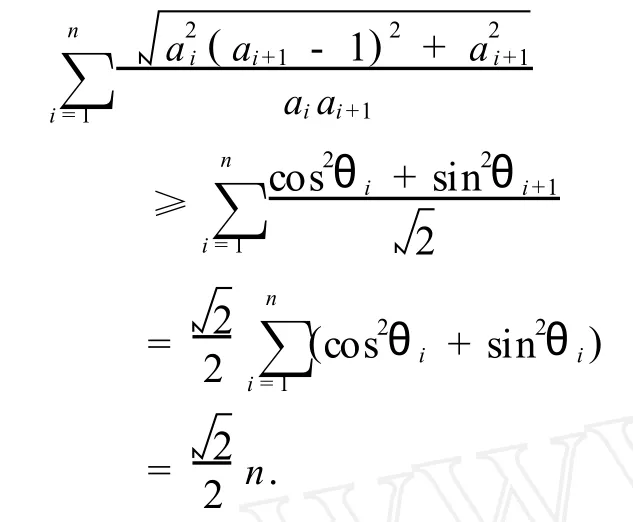
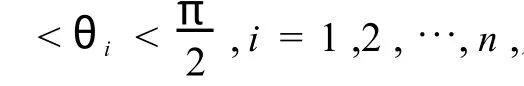
所以,

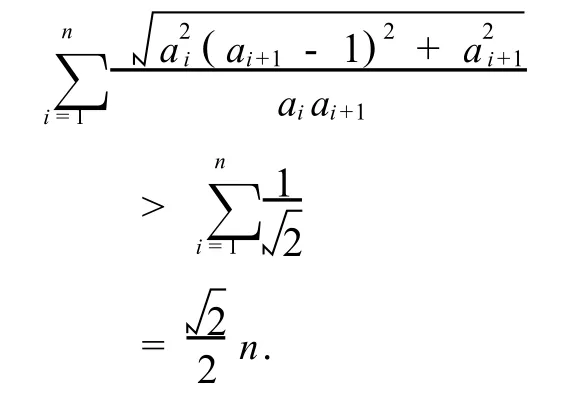
綜上,不等式(1)成立.

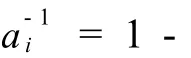
注釋1 相關的,我們可考究x,y＞1時,方程x+y=xy的解集.換言之,上面問題等價于考究X-Y平面上第一象限的單位正方形區域,S1:= {(x,y)||x|≤1;|y|≤1}之外,是否存在區域, S:={(x,y)|x＞1,y＞1,x+y=xy}.就幾何意義言之,如果存在這樣的點集,則它正好是平面,z =x+y,與馬鞍面,z=xy,的空間交線雙曲線的一部分,該部分在 X-Y平面上的投影是完全在第一象限內的那一支(如圖1,漸近線 x=1的右邊的實曲線).

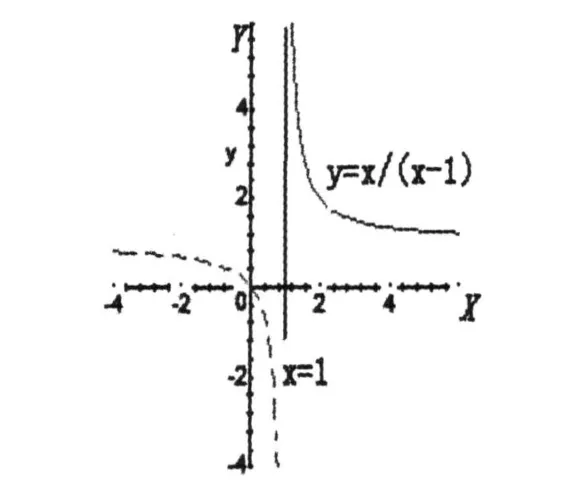
圖1 雙曲線在 X·-Y平面投影

綜上,使得不等式(2)取等號的,ai≥1,i=1,…,n,是雙曲線之右支實曲線上點的坐標,即(ai, ai+1)或(ai+1,ai),這里,ai≥1,i=1,…,n.值得注意的是,這種等式條件是頗有趣的一種!

注釋2 雖然第二證明并不簡明于第一證明,但三角代換帶來的變形還是頗為有趣的.或許這正是當初文獻[1]采用此方法的緣由.此外,通過嘗試,使用其他有別于上述的三角代換依然奏效!

定理2 如果,ai＞0,i=1,…,n,且p≥2,那么成立不等式,

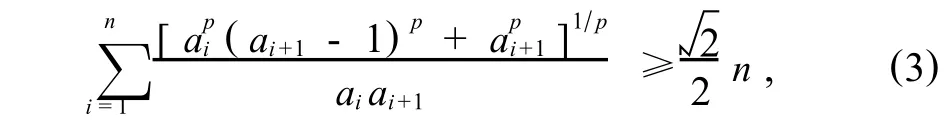
這里,an+1= a1.

事實上,使用上述幾乎為平行的敘述可以論證不等式(3).

[1]王向東,蘇化明,王方權.不等式·理論·方法[M].鄭州:河南教育出版社,1994.

[2]王挽瀾.建立不等式的方法[M].哈爾濱:哈爾濱工業大學出版社,2011.