參數估值的模糊Bayes方法探討

馬家蓉,徐 軍

(1.成都大學信息科學與技術學院,四川成都 610106;2.成都市城鄉建設委員會,四川成都 610031)

0 引 言

在工程中遇到的實際工程參數通常是一種變異性很大的各向異性體,工程設計施工中所需的參數,一般是依據實驗數據進行簡單統計分析,在處理具體問題時,樣本容量小,實驗數據離散大,其結果必然導致人為不確定.工程設計中根據可靠性理論[1]使用JC法求取破壞概率和可靠指標時,指定隨機變量的統計參數值和概率分布是必需的.就工程設計參數的概率分布推斷方法而言,一些學者對其進行了詳細研究[2-5].由于工程樣本通常是典型的隨機—模糊樣本,文獻[6]將工程樣本作為隨機模糊樣本,提出求解隨機模糊樣本均值和方差的公式.在此基礎上,本文提出以模糊數學原理和概率理論為基礎的模糊Bayes方法推斷參數特征值.

1 Bayes參數估值方法

Bayes參數估值法是根據Bayes統計理論引申而來,利用先驗分布信息,即利用已積累的某一參數的實驗資料,對分布概型進行初估,再根據后驗數據,即某一具體工程項目的有限實驗數據,對概率分布參數重新加以估計.該方法能夠較好地避免由于實驗數量不足引起的統計參數的偏差,并確定樣本參數的概率分析參數.

Bayes參數估值方法的具體步驟是,若設變量x的先驗密度函數為 f′(x),后驗密度函數為 f″(x),根據Bayes公式[3]有,

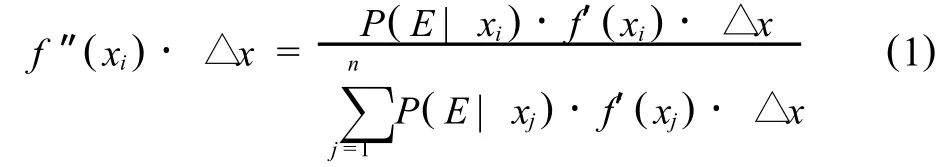
式中,P(E|xi)=P(E|xi≤x＜xi+△x),表示xm發生在區間(xi,xi+△x)上的實驗概率,E代表實驗結果,n代表試驗分段數.

直接應用上式計算后驗分布函數一般難以用解析式表達,故可假設后驗分布函數與先驗分布函數一致,然后確定變量的后驗分布函數.根據概率理論中均值與方差的定義,變量的后驗分布參數的均值與方差可近似為,

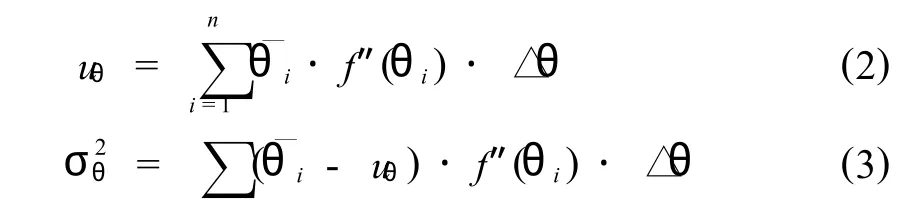
2 參數估值的模糊Bayes方法

2.1 參數樣本值隨機模糊分析

2.1.1 樣本參數均值.

取論域,U={x1,x2,…,xn},A—為 U上的一個模糊子集,論域中 U的元素xi對A—的隸屬度為uA(xi),則 A—的核 A1為,

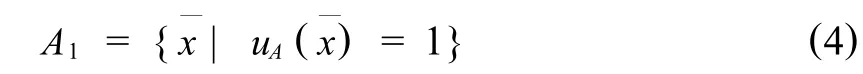
若上式的能夠表示為,

則此式即為所給某參數所具有的統計均值.

取樣本 xi對A的隸屬函數為,

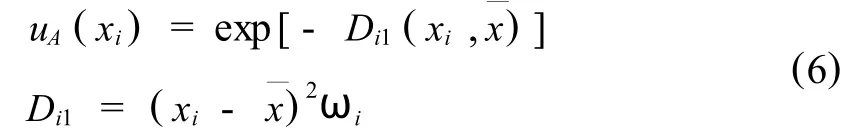
式中,xi為樣本值,x—為待求特征值,Di1是xi關于模糊集合A—的核的加權馬氏距離,ωi為權重,為方便起見,取,

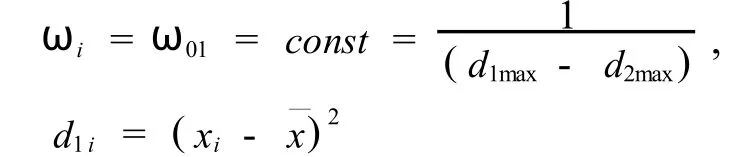
顯然,隸屬函數(6)具有這樣的規律:xi距x—的加權馬氏距離越大,則它對A—的隸屬度越小.隸屬函數確定之后,可按使實際樣本值整體上隸屬于樣本模糊子集A的程度最大的原則,建立并尋找所具有的統計特征值的目標函數,

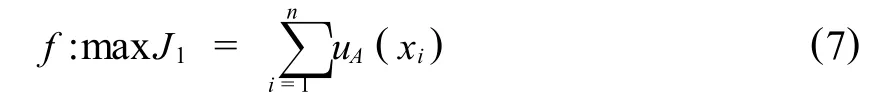
將式(6)代入式(7)得,

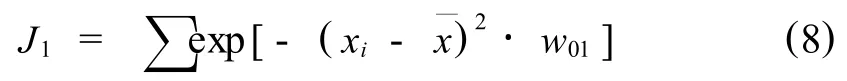
對式(8)有,

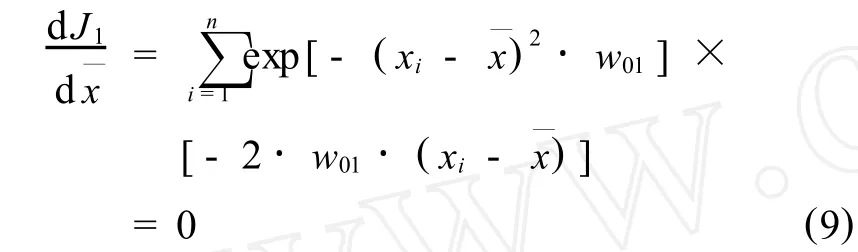
由式(9)得,

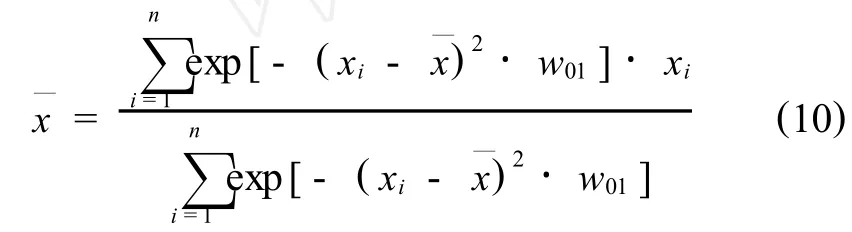
2.1.2 樣本方差.

設η是基于樣本值,U={x1,x2,…,xn},的隨機模糊變量,令,

取論域,

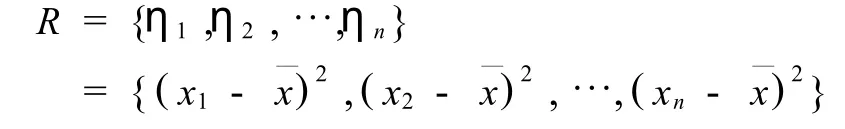
則,η對論域R上的模糊子集B—的隸屬函數為,

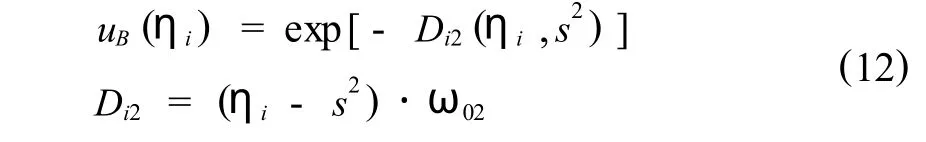
同理,可建立目標函數,

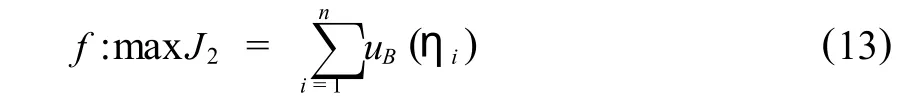
據此,可得樣本方差所服從的隨機模糊統計關系為,

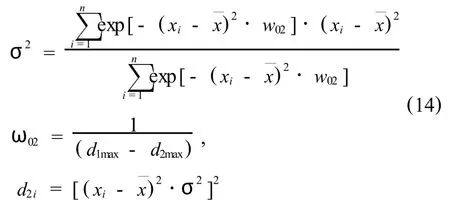
2.2 模糊Bayes方法確定樣本參數

設自然狀態集合為,S = {S1,S2,…,Sh}, P(Si)是自然狀態的先驗概率.下面討論有追加信息的場合,稱集合,X={x1,x2,…,xn},為信息源,設自然狀態為真的條件概率 P(xm|Sn)已經給出.由Bayes公式知道Sh的后驗概率為,

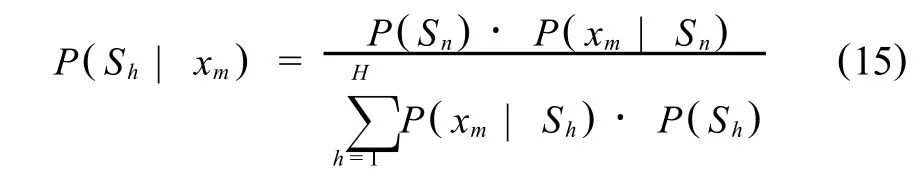
若信息源X中的每個信息本xm既是隨機又是模糊,則需要從中提取模糊信息.根據模糊事件概率的定義,模糊Bayes法則可表示為.

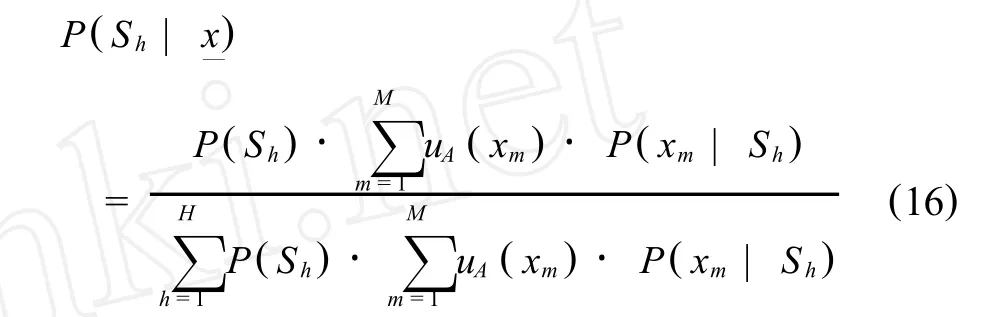
設變量x的先驗分布函數為f′(x),后驗分布函數為f″(x),則,

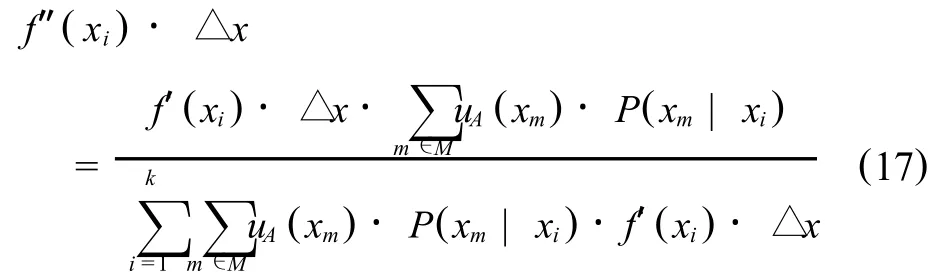
式中,P(xm|xi)= P(xm|xi≤x＜ xi+△x),表示 xm發生在區間(xi,xi+△x)上的實驗概率,xm代表實驗結果 ,K代表試驗分段數.

直接應用(17)式計算后驗分布函數一般難以用解析式表達,故可假設后驗分布函數與先驗分布函數一致,然后確定變量的后驗分布函數.

根據概率理論中均值與方差的定義,變量的后驗分布參數的均值與方差可近似由式(2)、(3)確定.至此,我們求得樣本參數特征值.

同時,不難證明,基于概率統計的Bayes方法是本文方法的一種特例.假設,X信息源不考慮其模糊性,則,

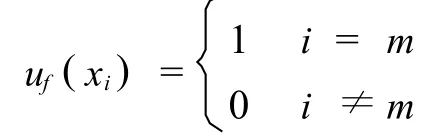
將其代入式(17),即為式(1).所以,模糊Bayes法是常規Bayes法的一個特例.

3 算 例

通過對國內95座已建土石壩工程建筑材料基本參數的統計,可得中壤土固結快剪 C服從極值I型分布樣本數據52個,均值18.0,標準差11.2,K,α分別為12.96 kPa,0.1145 kPa,現5組試驗如表1所示,求參數估值.

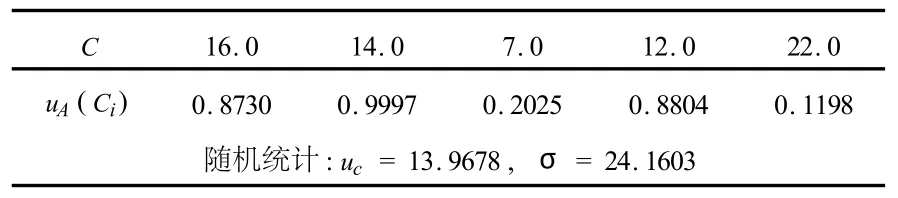
表1 參數隨機模糊處理結果

對以上試驗數據用模糊Bayes方法進行樣本參數估值:首先分5個區間,

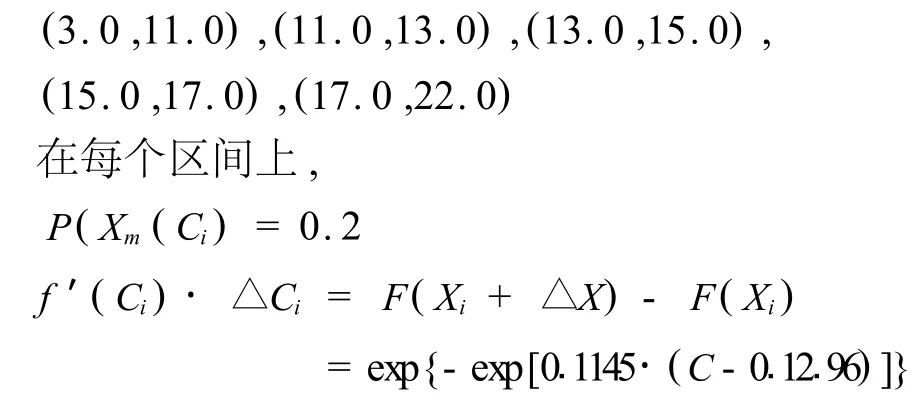
所以有,

由式(17)得,

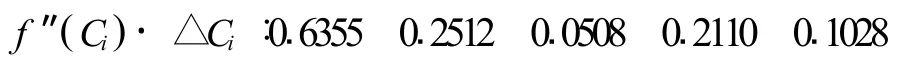
由式(2)、(3)得,

所以,

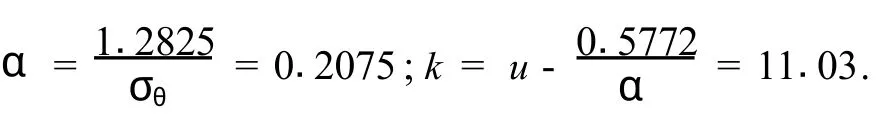
故,分布密度函數為,

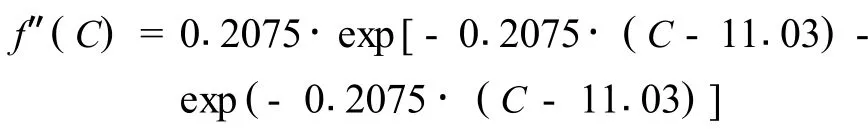
4 結 語

由于受地質運動、環境變化以及人類工程活動的影響,工程體的力學性質非常復雜,其本身的各種參數具有很大的不確定性.在進行工程可靠性分析時,通常會以一定的概率模型(概率分布函數或概率密度函數)來描述其力學參數所具有的不確性,對力學參數的概率分布特性研究始終是一項基礎性工作.本文將工程樣本作為典型的隨機 —模糊樣本,提出以模糊數學原理和概率理論為基礎的模糊Bayes方法推斷參數特征值,經具體工程項目的應用證明其是一種較有效的方法.

[1]吳世偉.結構可靠度分析[M].北京:人民交通出版社, 1990.

[2]徐超,楊林德.隨機變量擬合優度檢驗和分布參數Bayes估計[J].同濟大學學報,1998,26(3):340-344.

[3]張廣文,劉令瑤.確定隨機變量概率分布參數的推廣Bayes法[J].巖土工程學報,1995,17(3):91-94.

[4]徐軍,雷用,鄭穎人.巖土參數概率分布推斷的模糊Bayes探討[J].巖土力學,2000,21(4):394-396.

[5]李夕兵,宮鳳強.巖土力學參數概率分布的推斷方法研究綜述[J].長沙理工大學學報,2007,4(1):1-8.

[6]楊松林.工程模糊論方法及其應用[J].北京:國防工業出版社,1996.

[7]熊文林,李胡生.巖石樣本力學參數值的隨機—模糊處理方法[J].巖土工程學報,1992,14(6):101-108.