一種改進CORDIC算法的研究與實現

段素蓉

(西南交通大學信息科學與技術學院,四川成都 610031)

0 引 言

三角函數的坐標旋轉數字計算機(Coordinate Rotation Digital Computer,CORDIC)算法最早是由Volder于1959年提出,主要應用于實時導航的數字處理[1],通過擴展,該方法現已應用于眾多領域,如風力發電、航空航天、雷達信號處理、圖像處理、數字濾波以及通信設備等[2-4].

基本CORDIC算法的思路為:設定一個旋轉角度,經過多步旋轉迭代,最終計算出三角函數值.該方法由于迭代公式的選取限制了最大旋轉角度,所以旋轉角度不能覆蓋整個周期(-π～+π),導致部分角度計算出的三角函數值偏差較大,在應用中存在較大誤差[5-8].本文利用三角函數的對稱性,對輸入角度進行了預處理,把角度限制在基本CORDIC算法能正確計算的范圍內,再對迭代結果進行后處理,實現了完整周期(-π～+π)的三角函數計算.算法采用18級流水線結構實現,具有轉換速度快,精度高,占用資源少等特點.

1 CORDIC算法原理及改進

1.1 CORDIC算法原理

假設在直角坐標系下有向量(Xi,Yi),按圖1所示的方向旋轉角度θ得到向量(Xj,Yj),則二者關系為,

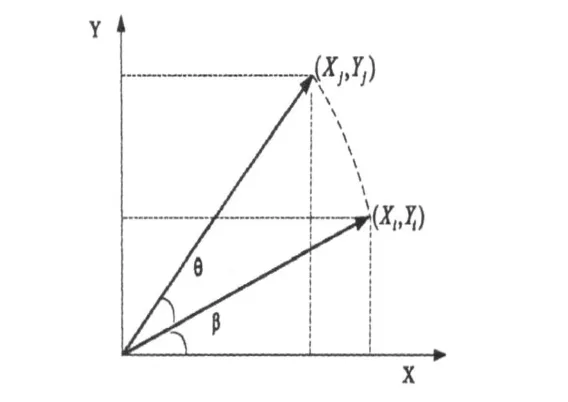
圖1 坐標旋轉圖

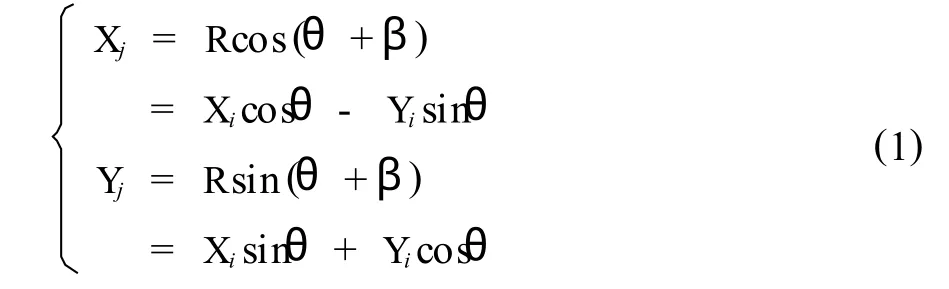
使用迭代的方法,坐標需要旋轉的角度可通過多步旋轉疊加完成(見圖2).根據多步旋轉疊加完成

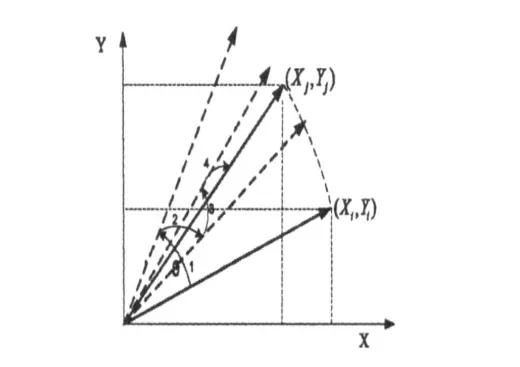
圖2 多次旋轉疊加示意圖

平面坐標旋轉,則式(1)可進一步轉化為,

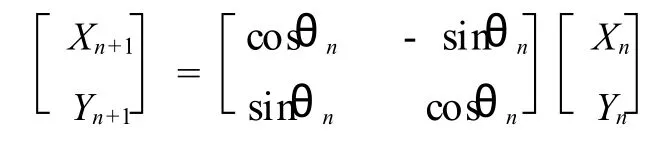
假設,tanθn= Sn/22,則,θn= Snarctan(1/2n).這里,Sn={-1;+1},當Sn=-1時,表示向量逆時針旋轉,否則為順時針旋轉.式(2)中的cosθn= cos(arctan(1/2n)).隨著旋轉次數的增加,該式收斂為一個常數,k≈0.607253.如果令 Y的初始分量為0,X的初始分量為單位1,則有,

當 n→∞時,CORDIC公式的輸出變為,

1.2 改進CORDIC算法設計

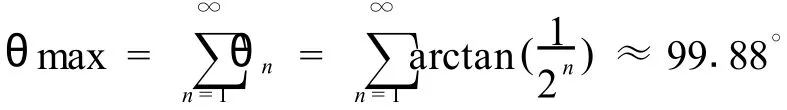
基本CORDIC算法旋轉角度總和為,即最大角度覆蓋范圍約為-99.88°≤θ≤99.88°.利用三角函數的對稱性,可把輸入角度限制在{-90°～90°},原理如下:

(1)若,θ≥0°,則θ′=θ-90°,否則,θ′=θ+ 90°,所以有,-90°≤θ′≤90°.

(2)根據三角函數變換公式,

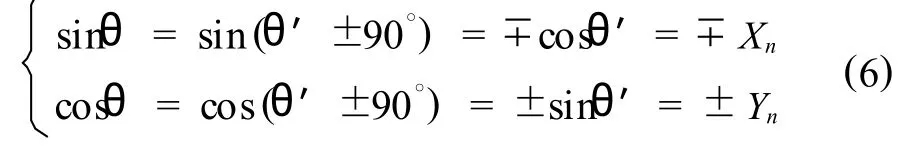
2 改進CORDIC算法實現及仿真測試

2.1 改進CORDIC算法的實現

改進CORDIC算法采用18級流水結構,各級間組合邏輯處理復雜度適中,處理速度快,能夠滿足風力發電變流器的控制系統坐標變換處理實時性要求.設計分為3個模塊.

(1)輸入角度預處理模塊.若輸入角度符號位為0,則減去90°,否則加上90°.設計中采用17 bit有符號數表示輸入角度.該模塊使用1級流水處理.

(2)基本CORDIC迭代模塊.迭代過程采用15級流水結構(見圖3),內部使用17 bit有符號變量,保證了運算精度高且運算過程不發生溢出,迭代中的乘法(1/2n)采用移位實現.該模塊使用15級流水處理.

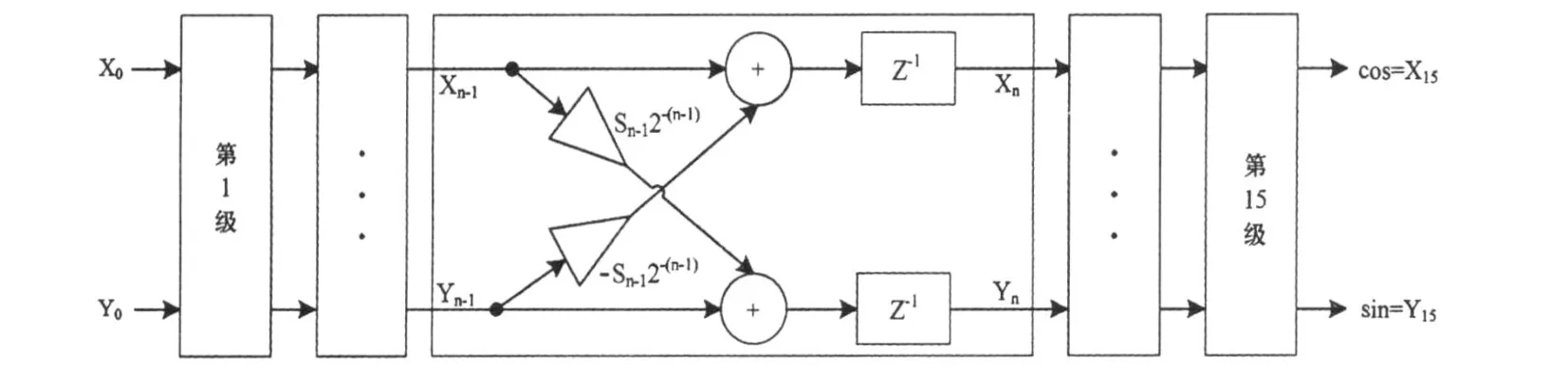
圖3 CORDIC算法流水線結構框圖

(3)迭代結果后處理模塊.將輸入角度符號位延時16級,與迭代結果對齊,根據延時后的符號位及式(6)對結果進行處理,同時對結果進行飽和處理,最后輸出16 bit有符號的三角函數值.該模塊使用2級流水處理.

圖4 改進前的CORDIC迭代三角函數值

2.2 改進CORDIC算法仿真驗證

(1)改進前后三角函數值仿真對比(輸入角度為-π～+π).

圖5 改進后的CORDIC迭代三角函數值

CORDIC算法改進前后三角函數值仿真對比如圖4、圖5所示.從圖4、圖5可以看出,改進后的CORDIC算法可以覆蓋完整周期(-π～+π)的三角函數計算,從而滿足了信號處理的需求.

(2)改進CORDIC算法精度對比.

改進前后CORDIC算法精度對比如表1所示.從表1的對比結果可以看出,改進CORDIC算法采用18級流水結構,內部使用17 bit有符號數進行計算,得到的結果精度高,誤差小于0.01%,完全可以滿足風力發電變流器的控制系統坐標變換處理的精度要求.

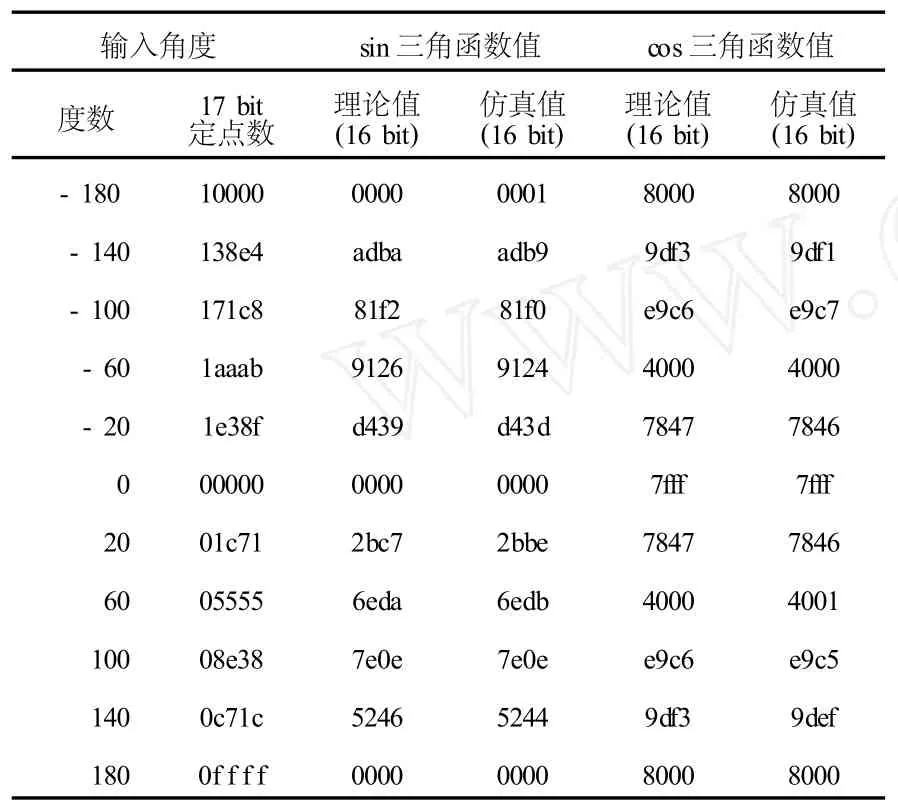
表1 改進型CORDIC算法仿真對照表

3 結 語

改進CORDIC算法克服了基本CORDIC算法不能覆蓋完整周期的三角函數計算的缺點,由于改進CORDIC算法采用18級流水線結構,且內部采用17 bit有符號定點數計算,保證了轉換速度快,運算結果精度高,易于用FPG A實現.仿真測試表明,改進CORDIC算法完全能滿足風力發電變流器系統控制中坐標變換處理的精度要求.

[1]Volder J E.The CORDIC Trigonometric Computing Technique [J].IRE Trans Electronic Computers,1959,8(3):330-334.

[2]Walther J S.A Unified Algorithm for Elementary Functions[C]// AFIPS71’Spring Joint Computer Conference.New Y ork:ACM Press,1971:379-385.

[3]徐國庫,陳禾.基于CORDIC算法的坐標變換電路的FPG A實現[J].微電子技術,2010,39(10):108-110.

[4]陳嫦娥,毛承雄.多相交流系統的PARK變換[J].高電壓技術,2008,34(11):2475-2482.

[5]王敏,薛忠杰.基于改進Cordic算法的NCO設計[J].電視技術,2011,35(5):30-33.

[6]湯文亮.基于CORDIC算法的高速高精度DDS研究與實現[J].制造業自動化,2011,33(3):104-106.

[7]文婧媛,徐欣峰.基于CORDIC算法的高速可配置FFT的FPG A實現[J].微電子學與計算機,2010,27(3):24-28.

[8]何曉華,謝建精,郭洪志,等.基于擴展收斂域CORDIC算法的FM信號數字化解調實現[J].電子技術應用,2010, 36(1)53-56.