路徑積分法在一類隨機動力系統中的應用

沈焰焰

(福建交通職業技術學院,福建福州 350007)

0 引 言

目前,考慮到非線性動力學系統有可能具有復雜的確定性響應及隨機響應,Yim等[1]及Naess等[2,5-7]利用隨機響應的概率密度分析混沌響應,即通過在具有確定性激勵的系統中引入隨機擾動,則確定性系統中的混沌吸引子的存在性可有效地利用隨機響應在相空間的概率密度的演化來描述.本文主要利用路徑積分法[2,5-7]研究一類非線性動力系統的混沌響應,計算了lévy噪聲激勵的混沌系統的瞬時概率密度、邊緣概論密度及平均概率密度[2].并討論了lévy噪聲對確定性系統混沌運動的影響.研究表明,在噪聲強度一定的情況下,隨機系統的概率密度的演化可以用來刻畫該混沌吸引算子的結構特征.

1 路徑積分法

在文獻[7]中,作者借助路徑積分法來尋求“非線性”FPK方程的形式解,并首先提出求解較高維FPK方程的路徑積分數值方法.這里“非線性”指的是FPK方程漂移向量和擴散向量對系統狀態變量的非線性依賴關系.之所以對形式解感興趣,是因為路徑積分能給出繞確定性路徑的近似解的適當初值點.最關鍵的一點是,路徑積分形式解可以在非平衡熱力學領域中延拓熱力學平衡概念,如熱力學勢能等.

路徑積分法的基本思想是,在空間和時間上分別離散化,以路徑和代替積分,即通過連接短時的轉移概率密度形成全局的轉移概率密度,得到狀態向量的聯合概率密度函數.路徑積分法最優越的特性在于可得到非負的、較準確的尾部概率密度.此外,路徑積分法還可以計算系統的非平穩瞬態概率密度以及首次穿越等問題[3,4].

定義路徑積分的最簡便方法是把連續過程離散化在空間和時間限定的充分小的網格點上.然而,一個連續過程的離散化并不唯一.因此,對于不同的離散規則,就產生了許多不同的路徑積分方法.為建立協變路徑積分,就需要選擇特定的離散化規則,這使得很多研究者致力于在不給出特定的離散化規則的情況下,提出各種推導協變路徑積分的方法.

2 考慮lévy噪聲對混沌運動的影響

本文嘗試著將高斯白噪聲改成lévy噪聲,采用的lévy過程是α-stable lévy過程[4].考慮如下的動力系統,

其中:γ,ζ,β都是正的;Lt是α-stable lévy噪聲,其強度為ζ.f0,α分別表示周期項系統的強度和頻率,當ζ=0時,方程(1)為確定性系統,

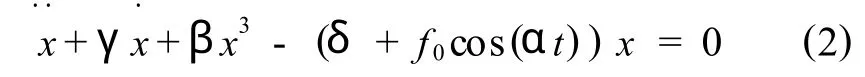
對于確定性系統,當參數取,

時可以得到確定性系統的時間歷程圖(圖1(a))、相軌圖(圖1(b))及Poincaré截面圖(圖1(c)).

本文中所用的Poincaré映射[3,4]均定義為,

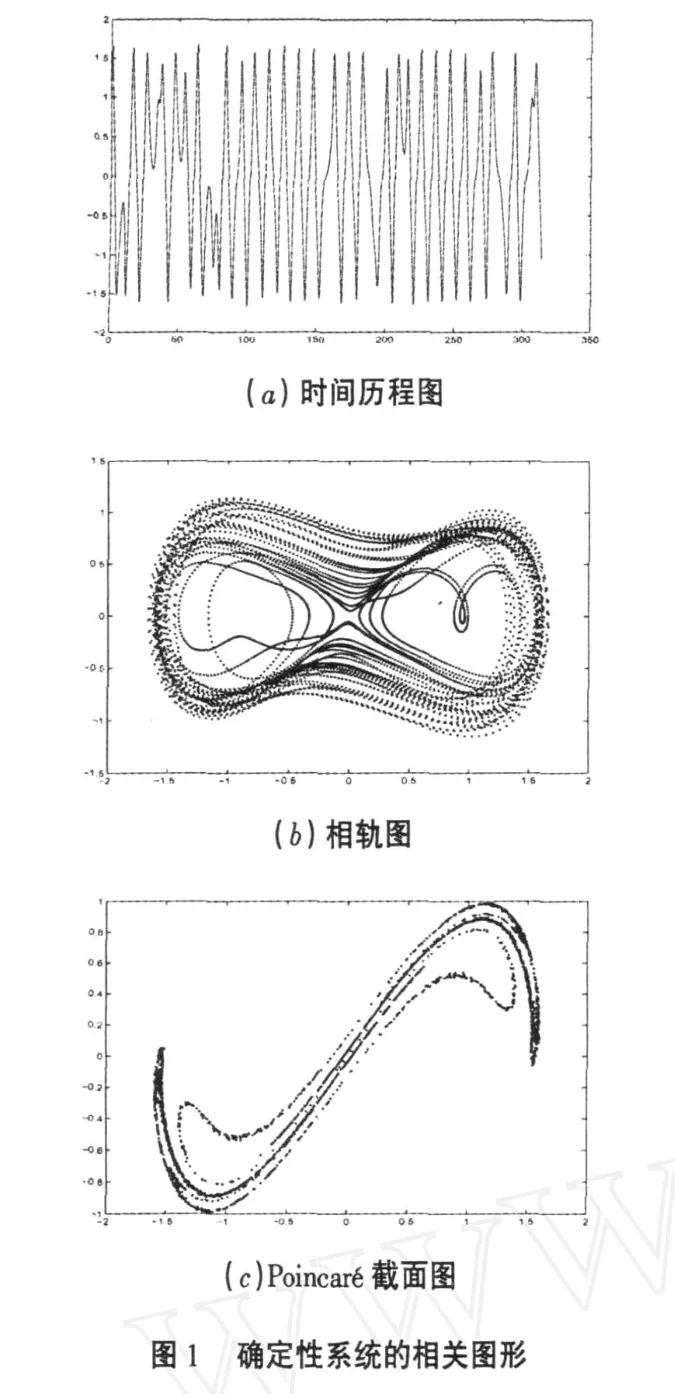
對于方程(2)所示確定性系統,可直接數值求解,并得出其Poincaré截面圖.在lévy噪聲情況下,當參數取值為式(3)及ζ=0.0005時,可得到相應的時間歷程圖(圖2(a)),相軌圖(圖2(b)),Poincaré截面圖(圖2(c)).

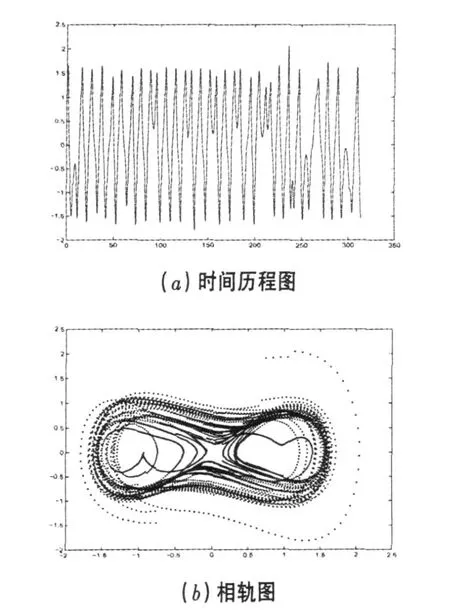
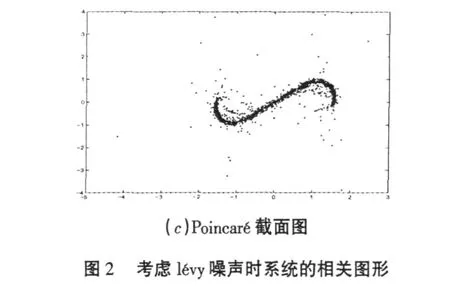
對比圖1(a)和圖2(a),我們可發現動力系統(1)的確定性系統的時間歷程圖和隨機激勵下系統的時間歷程圖是相似的,均呈現出無規則性.對比圖1(b)和圖2(b),可見確定性系統的相軌程圖和隨機激勵下系統的相軌圖也是相似的,但進一步觀察可以發現,確定性系統在隨機激勵的作用下,相軌圖稍微向外擴散,而且相對高斯噪聲的情況,擴散得更厲害.同樣對比圖1(c)和圖2(c)可以發現它們也是很相似的,確定性系統在隨機激勵的作用下, Poincaré截面圖有稍微向外擴散,但是相對高斯噪聲的情況,擴散得更厲害.基于上述的對比,可以認為:在一定強度的隨機激勵下,可以利用路徑積分的方法來確定非線性混沌系統.

下面利用路徑積分方法求解系統(1)在參數為,γ=0.3,β=1,δ=1,f0=0.6,α=1.2及ζ= 0.0005時,的瞬時概率密度函數、邊緣概率密度函等,結果如圖3～圖5所示.

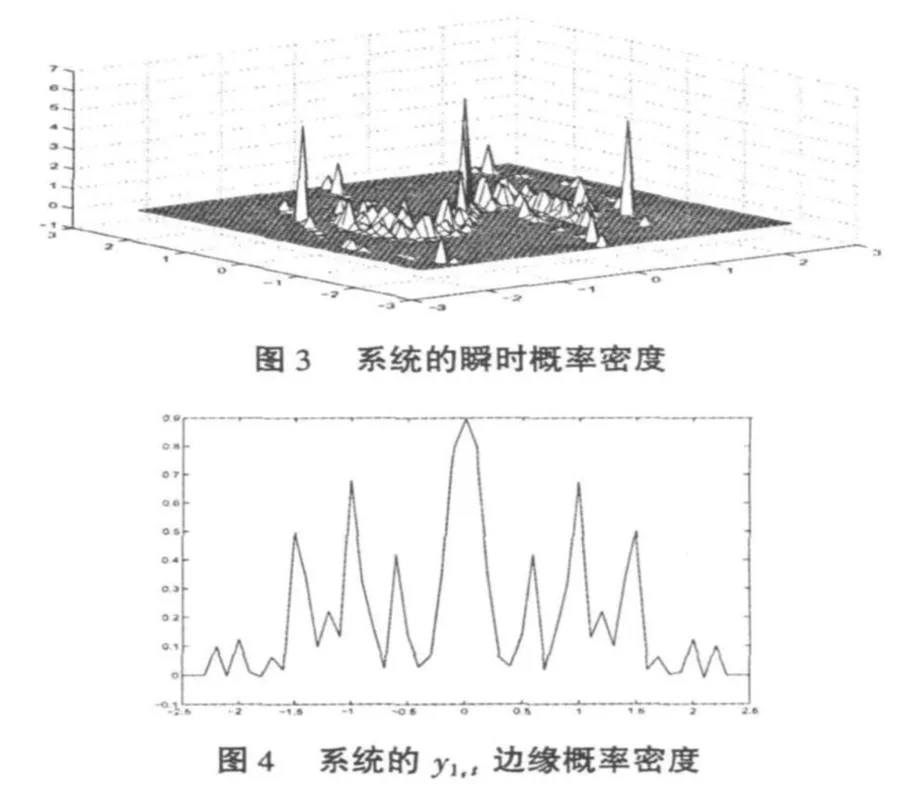
在參數為,γ=0.3,β=1,δ=1,f0=0.6,α= 1.2及ζ=0.0005時,圖3所示系統(1)的聯合瞬時概率密度,圖4表示系統(1)的y1,t邊緣概率密度分析,圖5表示系統(1)的 y2,t邊緣概率密度分布.

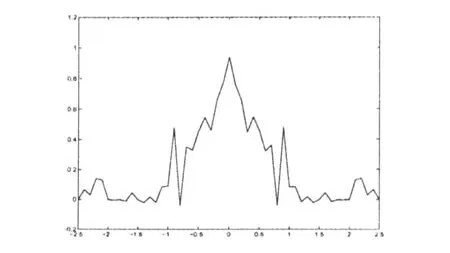
圖5 系統的 y2,t邊緣概率密度

與高斯白噪聲的情況一樣,在求得瞬時隨機系統的性質后,可進一步用隨機系統的概率密度形狀來表征相應的確定性系統的混沌吸引子的結構.考慮系統(1)在參數,γ=2,β=1,ω20=1,f0=0.3, α=1及ζ=0.0005時,應用,

可表征出關于時間平均的聯合概率分布(見圖6).

圖6 系統的聯合概率分布

3 結 論

本文嘗試把高斯白噪聲改成lévy噪聲,討論了受lévy噪聲激勵的動力系統混沌運動在參數為,γ =0.3,β=1,δ=1,f0=0.6,α=1.2及ζ=0.0005時,與確定性系統混沌運動的時間歷程圖、相軌圖及Poincaré截面圖的關系.結論表明,它們有著相似性.因此,我們可以用概率密度來解釋混沌吸引子的存在性,即借助隨機系統的概率密度在一定程度上刻畫了確定性系統的混沌吸引子.同時,我們也發現,由于lévy噪聲激勵對隨機噪聲的要求更嚴格,即lévy噪聲與高斯白噪聲相比,其噪聲強度要求相對更小,否則會使得確定性系統得到嚴重的破壞.

[1]Y im S C S,Lin H.Unified Analysis of Complex Nonlinear Motion via Densities[J].Nonlinear Dynamics,2001,24(1):103-127.

[2]Naess A.Chaos and Nonlinear Stochastic Dynamics[J].Probalistic Engineering Mechanics,2000,15(1):37-47.

[3]Moon F C.Chaotic and Fractal Dynamics:An Introduction for Applied Scientists and Engineers[M].New Y ork:Wilery&Sons Inc,1992.

[4]Samorodnitsky G,Taqqu M S.Stable Non-Gausian Random Processes[M].New Y ork:Chapman&Hall,1994.

[5]Naess A,JohnsenJ M.Response Statistics of Nonlinear Compliant Offshore Structures by the Path Integral Solution Method[J]. Probabilistic Engineering Mechanics,1993,8(1):91-106.

[6]Naess A,Moe V.Stationary and Non-stationary Random Vibraton of Oscillators with Bilinear Hysteresis[J].International Journal of Non-Linear Mechanics,1996,31(5):553-562.

[7]Naess A,Moe V.Efficinet Path Integration Mehtod for Nonlinear Dynamic Systems[J].Probabilistic Engineering Mechanics, 2000,15(4):221-231.