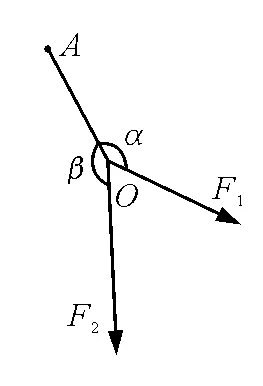
巧用圓討論力的合成和分解問題
程柱建
(如皋中學 江蘇 如皋 226500)
力的合成與分解遵循平行四邊形定則或三角形定則,有時巧用圓可以有效地討論有關力的合成和分解的解數、極值、大小和方向等問題.
1 求解數
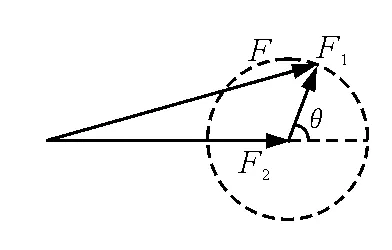
【例1】如圖1,已知合力F和一個分力F1的方向以及另一個分力F2的大小(F2的大小可根據解題需要自取),問F可以分解為幾組分力?
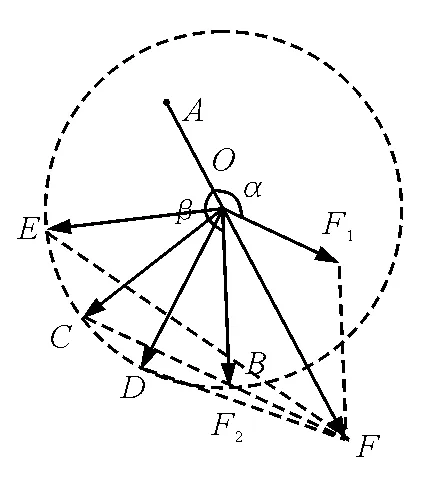
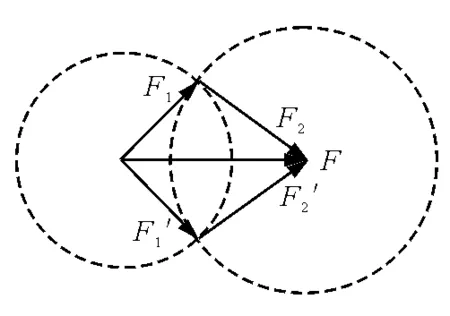
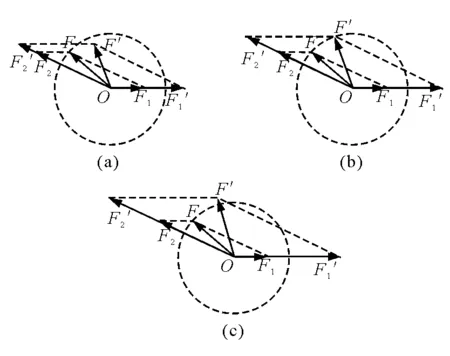
分析:以合力F的箭頭為圓心,以分力F2的大小為半徑畫圓.由于分力F1的方向確定,所以這個圓會與F1的作用線不相交、相切或相交三種情況,如圖2.根據三角形定則,F1、F2的交點指向合力,箭頭的有向線段表示分力F2.當F2 圖1 圖2 【例2】已知合力F和兩個不平行分力F1、F2的大小.三力的大小的關系滿足 |F1-F2| 問F可以分解為幾組分力? 圖3 分析:如圖3,以F的始端、末端為圓心,分別以F1、F2的大小為半徑畫圓,兩圓有兩個交點,這時,F分解為F1、F2有兩組解.由于兩分力沒有被限制在紙平面內,現以F為轉動軸旋轉,得到兩分力的方向有無數組解. 【例3】 (1)已知合力F和一個分力F1的方向,求另一個分力F2的最小值. (2)已知合力F的方向和一個分力F1,求另一個分力F2的最小值. 分析:(1)此題情境同例1中圓與F1相切的情況,這時兩分力垂直,F2的最小值等于Fsinθ. (2)如圖4所示,以分力F1的箭頭為圓心畫與F作用線相切的圓,即F2與F垂直時F2最小,最小值為F1sinθ. 圖4 圖5 【例4】一個物體受到兩個共點力F1、F2的作用,兩個力間的夾角可以變化,其中F1=100 N,F2=200 N.當兩個力的合力F與F2之間的夾角最大時,合力F為多大? 分析:如圖5所示,以F2的箭頭為圓心,F1的大小為半徑畫圓.根據三角形定則,連接F2始端、F1末端的有向線段表示合力F.旋轉F1,改變F1和F2的夾角,動態地觀察合力F與F2之間的夾角變化情況.當F與圓相切時,F與F2之間的夾角最大.此時 【例5】兩個分力F1、F2的大小不變,當夾角從零增大到180°的過程中,求合力F大小的變化. 分析:如圖6,保持F2不變,以F2的箭頭為圓心,以F1的大小為半徑畫圓,隨著兩分力夾角的增大,能清楚地看到合力F大小的變化情況,即θ增大,F減小. 圖6 【例6】若兩個力F1、F2的夾角為α(90°<α<180°),且α保持不變,則 A.一個力增大,合力一定增大 B.兩個力都增大,合力一定增大 C.兩個力都增大,合力可能減小 D.兩個力都增大,合力的大小可能不變 分析:為了方便比較,以兩力作用點O為圓心,以原合力F的大小為半徑畫圓,從圖7(a)、(b)、(c)中可以看出:當F1增大到F1′,F2增大到F2′時,合力F的大小可能減小、不變或增大,同理可知一個力增大時合力的變化也存在以上三種可能. 選項C、D正確. 圖7 【例7】橡皮條的一端固定在A點,另一端同時作用兩個力,使橡皮條伸長到O位置,這時兩個力F1、F2與OA夾角分別為α、β,如圖8所示(F1與F2間的夾角為銳角).現保持F2大小不變,β角減小一些,并仍保持橡皮條伸長到O位置.下列說法中可能發生的是 圖8 A.α減小,F1增大 B.α不變,F1增大 C.α增大,F1增大 D.α增大,F1減小 分析: 根據三力的平衡條件,F1、F2的合力F沿OA延長線的方向,利用平行四邊形定則可以畫出F.三個力中,F2大小不變,合力F的大小、方向不變(因為要保持橡皮條伸長到O位置). 如圖9,以O點為圓心,以F2的大小為半徑畫圓,初始F2的箭頭與圓交于B點,過B點作初始F1的平行線,與圓交于C點,C點是F1方向變化的臨界點.當F2的箭頭沿圓弧BC左移時,α角比初始值小;F2指向C點時,α角等于初始值;F2的箭頭沿圓弧從C點左移時,α角比初始值大.連接F2箭頭和F箭頭的有向線段表示F1,可以看出在β角減小的過程中F1一直增大. 選項A、B、C正確. 圖9 總之,在力大小不變,方向不確定時,利用圓與平行四邊形定則或三角形定則,往往可以便捷地討論力的合成與分解問題.本文對圓的使用技巧也可以遷移到其他矢量的合成與分解的應用中;如“小船過河”問題中,當v船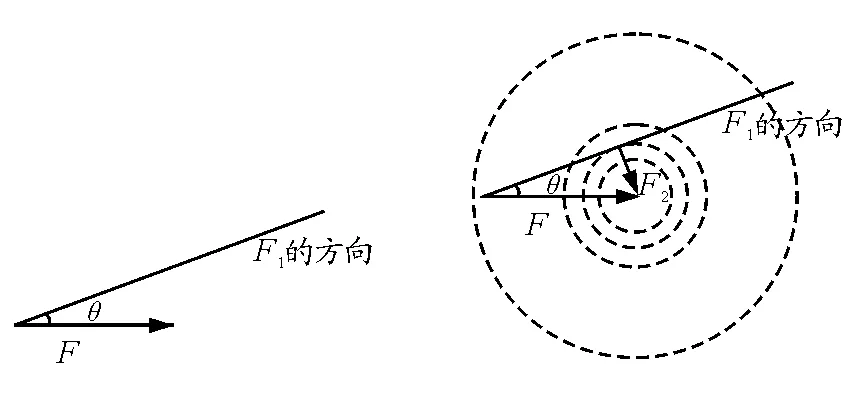
2 找極值

3 比大小
4 看方向