關于扭擺法測轉動慣量實驗的改進
池紅巖 丁紅偉
(黑龍江科技學院實訓中心 黑龍江 哈爾濱 150027) (黑龍江科技學院理學院 黑龍江 哈爾濱 150027)
1 引言
轉動慣量是剛體轉動時慣性大小的量度,是表征剛體特性的一個重要物理量[1~5].剛體轉動慣量除了與物體質量有關外,還與轉軸位置和質量分布有關.對于形狀簡單、質量分布均勻的剛體的轉動慣量可以通過計算獲得.在工程實踐中常常需要知道一些形狀復雜、質量分布不均勻的剛體轉動慣量的大小,例如機械部件、電動機轉子、飛機螺旋槳和槍炮的彈丸等.為此需要通過實驗進行測量,而在實驗室中一般采用扭擺法.但用扭擺法測物體轉動慣量的系統誤差較大.本文針對傳統扭擺法測物體轉動慣量系統誤差較大的缺點,在扭擺的改進和實驗數據的處理方面提出了行之有效的方法.
2 實驗裝置及原理
轉動慣量測試儀本質上是一個周期記錄儀,它由兩部分組成:主機和光電傳感器,如圖1所示.主機主要由螺旋彈簧、水平儀、扭擺主軸和止動螺絲組成.其中螺旋彈簧產生恢復力矩,使被測物體繞平衡位置擺動;水平儀調節基座上的底腳螺絲使水準泡中氣泡居中;扭擺主軸和止動螺絲用以固定待測物體.而光電傳感器的作用是把光信號轉換成電信號,當被測物體上的擋光桿第一次通過光電傳感器的光電門時,相當于給光電傳感器一個光信號,傳感器將光信號轉換成電信號,傳給主機并開始記錄.

圖1 傳統轉動慣量測量儀
扭擺法測物體轉動慣量的實驗原理很簡單,主要是利用剛體力學[6~7]的知識.其中螺旋彈簧提供的恢復力矩M和所轉過的角度θ成正比,即
M=-κθ
(1)
式中κ為彈簧的勁度系數.依據轉動定律
M=Iβ
(2)
式中I為物體的轉動慣量,β為角加速度.
根據上述兩式可得
(3)
上述方程表示扭擺運動具有角簡諧振動的特性,角加速度與角位移成正比,且方向相反,此方程的解為
θ=Acos(ωt+φ)
式中A為諧振動的角振幅,φ為初相位角,ω為角頻率.此諧振動的周期為
(4)
由(4)式可知,只要實驗測得物體扭擺的擺動周期,在I和κ任一個量已知的情況下,即可計算出另一個量.
3 傳統扭擺法存在的缺陷及改進措施
原有的扭擺的擋光桿都位于待測物體上,這一方面使待測物體本身的轉動慣量比自身真實值有所增加,造成誤差較大;另一方面由于系統本身受摩擦阻力、擺角大小以及彈簧的勁度系數等因素的限制,系統誤差不宜有效的弱化.為此,在原扭擺的基礎上多加了一個帶擋光桿的金屬圓盤,固定在扭擺的垂直軸上,如圖2所示.在它的上方是用于固定待測物體的止動螺絲.經過這樣改進以后,一方面消除了待測物體由于擋光桿本身的額外轉動慣量附加值,從而減小了誤差;另一方面由摩擦、擺角大小以及彈簧的勁度系數等引起的系統誤差在一定程度上被弱化了.
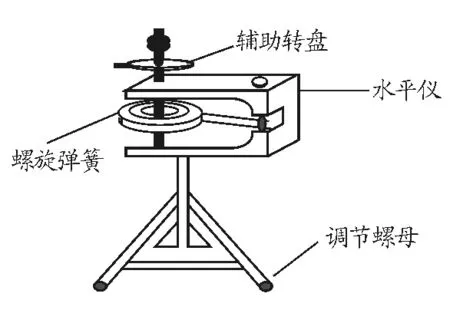
圖2 改進的轉動慣量測量儀
實驗結果如表1所示.對實驗室中的圓柱體和木球的轉動慣量分別用改進前后的儀器進行測量.改進前圓柱體轉動慣量的實驗值和理論值的百分比為90.37;改進后為99.61.木球的轉動慣量在改進前后分別為86.77和98.21.實驗數據充分顯示了改進后的轉動慣量測量儀在一定程度上弱化了系統誤差.

表1 改進前后實驗數據比較
4 結論
對傳統扭擺法的改進,可以獲得更精確的實驗值,主要在于它在一定程度上弱化了系統的誤差.改進后的方法比較簡單,便于學生自己動手實現.另一方面,對那些和實驗室中金屬盤相比較,轉動慣量偏小的物體進行測量時,反而在測量中出現誤差反彈的現象,這也暴露出我們改進后的扭擺有一定的適用范圍.
1 李曉萍,任常愚,尹向寶.大學物理學. 北京:機械工業出版社,2009.50~60
2 唐炳華,趙世杰. 大學物理學.北京:學苑出版社,1994.172~199
3 程守洙,江之水.普通物理學.北京:高等教育出版社,1982.218
4 費曼.費曼物理學講義.上海:上海科學技術出版社,1981.167~174
5 趙凱華,等.新概念物理教程·力學.北京:高等教育出版社,1995
6 吳乃爵,等.工科物理實驗教程.杭州:浙江大學出版社,1991
7 陳守川,等.大學物理實驗教程. 杭州:浙江大學出版社,1983

