利用動(dòng)態(tài)圓破解磁偏轉(zhuǎn)極值(范圍)問(wèn)題
——追憶2010年全國(guó)高考理綜卷(Ⅰ)(Ⅱ)物理壓卷題影蹤

張維軍

(會(huì)寧縣第二中學(xué) 甘肅 會(huì)寧 730700 )

帶電粒子在有界勻強(qiáng)磁場(chǎng)中運(yùn)動(dòng)，若其軌跡是一段圓弧，電磁學(xué)上則把這種運(yùn)動(dòng)稱為磁偏轉(zhuǎn).磁偏轉(zhuǎn)問(wèn)題是高考的熱點(diǎn)，可以很好地考查學(xué)生的理解能力、分析綜合能力，特別是應(yīng)用數(shù)學(xué)處理物理問(wèn)題的能力，而其中極值(范圍)問(wèn)題又是這類問(wèn)題中的難點(diǎn).

極值(范圍)的產(chǎn)生通常源于兩種情形：第一種，由帶電粒子進(jìn)入磁場(chǎng)時(shí)速度大小(或粒子比荷)不確定所導(dǎo)致；第二種，由帶電粒子進(jìn)入磁場(chǎng)時(shí)速度方向不確定所導(dǎo)致.要解決此類極值(范圍)問(wèn)題，探尋臨界軌跡圓，確定臨界點(diǎn)是關(guān)鍵.對(duì)于第一種情形，可采用動(dòng)態(tài)“縮放圓”的方法確定；對(duì)于第二種情形，可采用動(dòng)態(tài)“旋轉(zhuǎn)圓”的方法確定.

下面筆者舉例說(shuō)明在備考沖刺階段是如何引導(dǎo)學(xué)生增強(qiáng)解題質(zhì)量，從而提高解題能力的.

1 考前模擬預(yù)猜演練

【例題1】[天智達(dá)高考特快信息調(diào)研卷(二)T4 (07)]如圖1所示，在正三角形區(qū)域內(nèi)存在著方向垂直于紙面向外、磁感應(yīng)強(qiáng)度大小為B的勻強(qiáng)磁場(chǎng)，一個(gè)質(zhì)量為m、電荷量為+q的帶電粒子(重力不計(jì))從AB邊的中點(diǎn)O以速度v進(jìn)入磁場(chǎng)，粒子進(jìn)入磁場(chǎng)時(shí)的速度方向垂直于磁場(chǎng)且與AB邊的夾角為60°.若粒子能從AB邊穿出磁場(chǎng)，則粒子在磁場(chǎng)中運(yùn)動(dòng)的過(guò)程中，粒子到AB邊的最大距離為

圖1

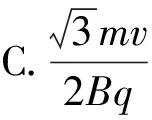
解析:本題中帶電粒子進(jìn)入磁場(chǎng)時(shí)速度方向是確定的，則粒子做圓周運(yùn)動(dòng)的軌跡圓圓心一定在垂直于初速度的射線上.為了找到臨界軌跡圓，確定臨界點(diǎn)，應(yīng)讓粒子的速率逐漸變大，粒子運(yùn)動(dòng)的軌跡，即為半徑逐漸變大的一系列動(dòng)態(tài)圓，相當(dāng)于把軌跡圓逐漸放大，如圖2所示.從軌跡圓的動(dòng)態(tài)縮放中就可以發(fā)現(xiàn)臨界軌跡圓，確定臨界點(diǎn).

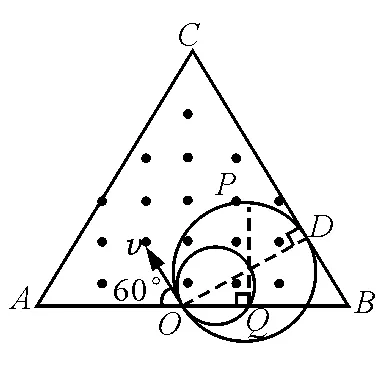
圖2

粒子進(jìn)入磁場(chǎng)后發(fā)生磁偏轉(zhuǎn)，滿足粒子能從AB邊穿出磁場(chǎng)且在磁場(chǎng)中運(yùn)動(dòng)過(guò)程中，到AB邊有最大距離的臨界軌跡圓必與BC相切于D.設(shè)臨界半徑為R0，由幾何關(guān)系可得

代入

即可知選項(xiàng)B正確.

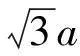
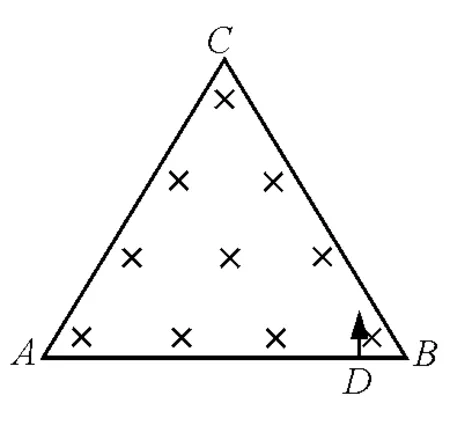
圖3

解析:此題只是將例1的初始條件改變，具體分析如圖4.解題的思路不變，如圖5.

圖4

圖5

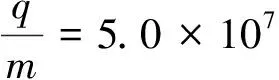
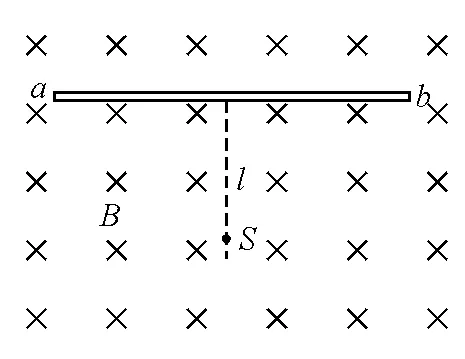
圖6

解析:本題中粒子進(jìn)入磁場(chǎng)時(shí)的速度大小是確定的，則所有粒子運(yùn)動(dòng)的軌道半徑相同.但粒子進(jìn)入磁場(chǎng)時(shí)的速度方向發(fā)生改變，會(huì)發(fā)現(xiàn)粒子的圓心位置不同：所有粒子的圓心都在以入射點(diǎn)S為圓心、以軌道半徑為半徑的圓——“圓心圓”上.為了找到臨界軌跡圓，確定臨界點(diǎn)，應(yīng)以圓心圓的不同位置為圓心畫出半徑相同的一系列動(dòng)態(tài)圓，相當(dāng)于把軌跡圓位置繞定點(diǎn)S旋轉(zhuǎn)，如圖7，從軌跡圓的動(dòng)態(tài)旋轉(zhuǎn)中即可發(fā)現(xiàn)臨界軌跡圓，確定臨界點(diǎn).

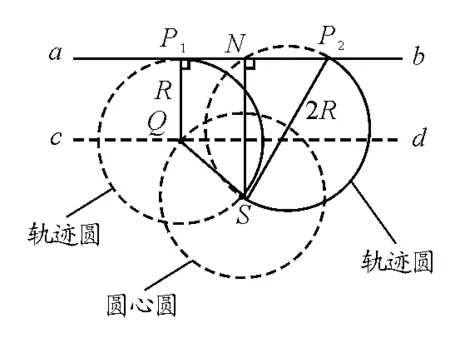
圖7

因α粒子帶正電，故軌跡圓應(yīng)繞定點(diǎn)S沿逆時(shí)針?lè)较蛐D(zhuǎn).根據(jù)

代入數(shù)據(jù)解得

R=10 cm

可見(jiàn)

2R>l>R

為確定ab上被α粒子打中的區(qū)域的長(zhǎng)度，先考慮N的右側(cè)，右側(cè)最遠(yuǎn)點(diǎn)應(yīng)是α粒子偏轉(zhuǎn)運(yùn)動(dòng)半個(gè)圓周后與ab相接的點(diǎn)P2(為軌跡圓的直徑與ab的交點(diǎn))，有

(1)

再考慮N左側(cè)最遠(yuǎn)點(diǎn).當(dāng)軌跡圓逆時(shí)針旋轉(zhuǎn)到與ab相切時(shí)，則切點(diǎn)P1就是α粒子能打中的左側(cè)最遠(yuǎn)點(diǎn).為確定P1點(diǎn)的位置，可作與ab相距為R且平行于ab的直線cd，交圓心圓于Q，再過(guò)Q作ab的垂線，垂足即為P1，有

(2)

由(1)、(2)式得所求長(zhǎng)度為

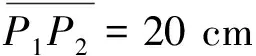
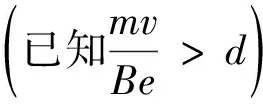
圖8

解析:分析可知該題符合第二種情形，如圖9所示.經(jīng)過(guò)進(jìn)一步作圖分析可知，當(dāng)軌跡圓弧對(duì)應(yīng)的弦長(zhǎng)為d時(shí)有最短時(shí)間，如圖10，于是

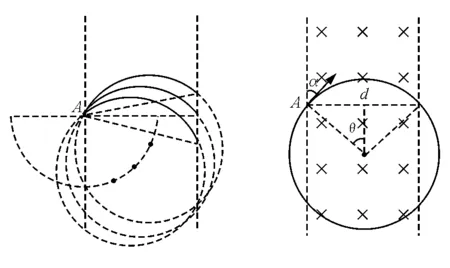
圖9 圖10

2 高考全真試題

圖11

【試題1】(2010年全國(guó)高考卷Ⅱ第26題)圖11中左邊有一對(duì)平行金屬板，兩板相距為d,電壓為U；兩板之間有勻強(qiáng)磁場(chǎng)，磁感應(yīng)強(qiáng)度大小為B0，方向平行于板面并垂直于紙面朝里.圖11中右邊又有一邊長(zhǎng)為a的正三角形區(qū)域EFG(EF邊與金屬板垂直)，在此區(qū)域內(nèi)及其邊界上也有勻強(qiáng)磁場(chǎng)，磁感應(yīng)強(qiáng)度大小為B，方向垂直于紙面朝里.假設(shè)一系列電荷量為q的正離子沿平行于金屬板面、垂直于磁場(chǎng)的方向射入金屬板之間，沿同一方向射出金屬板之間的區(qū)域，并經(jīng)EF邊中點(diǎn)H射入磁場(chǎng)區(qū)域.不計(jì)重力.

(1)已知這些離子中的離子甲到達(dá)磁場(chǎng)邊界EG后，從邊界EF穿出磁場(chǎng)，求離子甲的質(zhì)量.

(3)若這些離子中的最輕離子的質(zhì)量等于離子甲質(zhì)量的一半，而離子乙的質(zhì)量是最大的，問(wèn)磁場(chǎng)邊界上什么區(qū)域內(nèi)可能有離子到達(dá)?

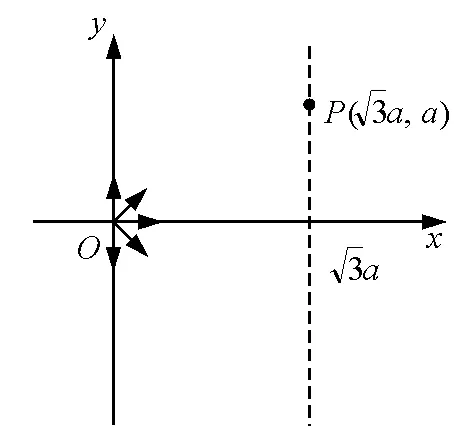
圖12

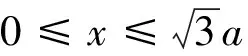
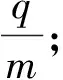
(2)此時(shí)刻仍在磁場(chǎng)中的粒子的初速度方向與y軸正方向夾角的取值范圍；

(3)從粒子發(fā)射到全部粒子離開(kāi)磁場(chǎng)所用的時(shí)間.

3 考后加強(qiáng)反思積累經(jīng)驗(yàn)

兵不在多而在精.解題就像游泳﹑滑冰、彈鋼琴，是一種實(shí)踐性技能，這種技能只有通過(guò)模仿和實(shí)踐才能學(xué)好.所以適量的解題是必要的.要通過(guò)量變引起質(zhì)變，達(dá)到熟能生巧的境地.但解題也不是“多多益善”，這是因?yàn)榫帉懙念}目可以千變?nèi)f化，高考題又幾乎都是原創(chuàng)題，靠死記硬背的“題海戰(zhàn)術(shù)”是不可能獲得高考成功的.要成功，關(guān)鍵在于教師要引導(dǎo)學(xué)生真正做到以下三點(diǎn).

(1)“獨(dú)立”解題

解題時(shí)常得到“外援”的學(xué)生，一旦在考場(chǎng)中孤軍作戰(zhàn)時(shí)，就會(huì)感到力不從心、斗志缺失.所以平時(shí)解題時(shí)，尤其是遇到過(guò)去沒(méi)有遇到過(guò)的“生題”時(shí)，一定要樹立信心，克服“畏懼物理”的心理.要有“勇氣”，特別是要有“興趣”去研究它，不要輕易放棄也不要輕易求助于別人.即使在短時(shí)間內(nèi)不能解決，仍要堅(jiān)持“一定要靠自己去解決它”的頑強(qiáng)精神，慢慢地把問(wèn)題解決，只有這樣在自己克服困難、刻苦鉆研的過(guò)程中，解題能力才能得到有效提高.

(2)要追求“真會(huì)”

把一道題做出來(lái)只是第一步.明白為什么這樣做是第二步.第三步是能把這個(gè)解法講得清楚.只有這三步都會(huì)了才是“真會(huì)”.真會(huì)做一道題比囫圇吞棗做幾十道題更有效.真會(huì)了就不怕題目千變?nèi)f化，就能以不變應(yīng)萬(wàn)變.

(3)注意“通性通法”不要過(guò)多追求“巧解巧法”

通性通法具有遷移性和應(yīng)用性.通性通法解題顯得自然流暢，易于思考，也容易交流.而“巧解巧法”都是平時(shí)反復(fù)推敲，多方試探的結(jié)果，一般不具有遷移性，也許只是“妙手偶得之作”；這樣的“境界”往往可遇而不可求.所以平時(shí)的解題應(yīng)以通性通法為根本方法，而不能反過(guò)來(lái)舍本逐末.當(dāng)然，通法與技巧也是相對(duì)的，有的巧法不光能針對(duì)某個(gè)題目而是能針對(duì)某一類題目，那它也就成了一個(gè)通法了.