一種形狀多級描述方法及在多尺度空間數據幾何相似性度量中的應用

安曉亞，孫 群，肖 強，嚴薇，2

1.信息工程大學測繪學院，河南鄭州450052；2.61512部隊，北京100088

1 引 言

空間數據幾何相似性度量模型被廣泛應用于地理信息科學的眾多領域，根據應用，將其分為兩類：第一類用于度量不同目標之間的幾何相似性，主要應用于空間數據匹配［1－6］，其實質是從指定數據集中找到一個與待匹配對象在空間位置、方向、大小、長度和形狀上最相似的目標，最終識別不同數據集上的同名實體［4］；第二類主要應用于同一目標在數據處理前后變形程度的度量［7－8］。上述應用中，多尺度幾何形狀相似性度量難度最大，其關鍵是形狀描述子對形狀的整體和局部特征都要能刻畫，即滿足緊致性，如第一類模型要求描述子盡量對形狀的整體特征進行描述，而第二類模型要求描述子必須顧及尺度的變化，對局部細節特征更要考慮。目前有代表性的形狀描述方法及其特點是：簡單描述子對復雜形狀的描述明顯不足，中心距離對角度函數僅能刻畫全局特征，單一的傅里葉描述對噪聲敏感，小波描述嚴重依賴于形狀起始點，形狀上下文描述僅能刻畫局部特征［7－11］。文獻［1—6］基于第一類模型進行數據匹配，但很難達到相似度量結果不受尺度變化影響，文獻［4］提出以中心距離對弧長的函數來描述幾何形狀，在同比例尺數據匹配中效果較好。

對此，提出一種具備對形狀多級描述能力的新方法，既能以較詳細的程度刻畫形狀，同時通過調節相關參數也能以較概略的程度刻畫形狀，可以達到通用于兩類模型的目標。基于該方法，建立通用多尺度相似性度量模型，并將它們分別應用于多尺度數據匹配和圖形化簡前后的相似性度量中。

2 形狀的多級描述方法

將形狀輪廓表示為一組有序點集：A＝｛Pi＝（xi，yi）｜i＝1，2，…，N｝（圖1（a）），O為幾何中心，從Pi出發，沿逆時針將A按弧長等分為K個弧段，K為偶數，Gt（t＝1，2，…，K－1）是對應等分點。連接Pi與Gt，得到K－1條弦｛PiG1，PiG2，…，PiGK－1｝，lt（Pi）表示Pi對應第t條弦PiGt的弦長。s（Pi）表示O到Pi的中心距離。當Pi在輪廓線上改變時，每一個Pi對應一個lt（Pi）和s（Pi），故lt（Pi）和s（Pi）是Pi的函數。設P0為起始點，則Pi可表示為弧的長度ci。以ci為自變量，lt（Pi）和s（Pi）可表示為ci的函數Lt（ci）和S（ci）。至此，A可由自變量弧長ci、因變量弦長Lt（ci）和S（ci）來描述。對于線目標（圖1（b）），如果lAB／cAB≥0.5，尋找一點O，使△OAB為等邊三角形，然后以O為幾何中心，計算s（Pi），在計算lt（Pi）時，將△OAB看作面目標，然后依據圖1（a）的方法計算；如果lAB／cAB＜0.5，直接連接首末點A、B，將其轉化為面目標按圖1（a）的方法計算lt（Pi）和s（Pi）。

圖1 多級弦長Fig.1 Multilevel chord length

一個ci對應弦長函數L1（ci），L2（ci），…，LK－1（ci）有K－1個，其中，ci∈［0，C］，C為輪廓線周長。將有序集合F（ci）＝｛L1（ci），L2（ci），…，LK－1（ci）｝稱之為ci對應的多級弦長函數，Lt（ci）表示ci對應的第t級弦長函數。當t＝K／2時，LK／2（ci）是輪廓線1／2弧長對應的弦長，當t大于K／2時，無法將輪廓線整數等分，因此，將F（ci）壓縮一半為F（ci）＝｛L1（ci），L2（ci），…，LK／2（ci）｝，只包含K／2級弦長函數。

上述描述方法滿足旋轉和平移不變性，用C對ci進行歸一，然后以S（ci）和Lt（ci）的均值對它們進行歸一化后可滿足縮放不變性。

3 相似性度量模型建立及應用

3.1 利用多級描述方法度量形狀相似性

多級弦長函數描述形狀滿足緊致性。以圖2為例，計算兩圖當K＝8時的4級弦長函數，并繪制曲線進行對比，圖3為1～4級弦長曲線。計算當橫坐標取同一數值（從0開始到1，間隔為0.05）時每幅圖對應兩曲線縱坐標的差值，求這些差值序列對應的標準差s，分別為0.16、0.11、0.08和0.05，標準差越大，說明兩形狀越不相似，反之則否。經第一級弦長函數描述的兩形狀最不相似，說明對細節信息能很好地刻畫，第2、3級弦長函數的相似性逐漸增大，到第4級弦長函數，兩曲線已非常接近，說明對整體形狀相似性能有效地描述。因此，可以利用多級描述方法來度量不同尺度空間數據的形狀整體或者局部相似性。

圖2 整體相似而細節有較大差異的兩個形狀Fig.2 Two shapes have whole similarity and local difference

圖3 圖2中兩形狀的4級弦長曲線Fig.3 4levels chord length curve for Fig.2

之所以可以采用上述方法利用標準差直接度量兩形狀的相似性，是因為兩形狀的起始點位置基本一致，且采樣相同的輪廓線點數20。但在實際應用中，兩形狀起始點位置不一定一致，且輪廓線點數也不相等，導致每一級弦長函數的個數不一致，無法進行比較。為此，通過以下方法來改進：

（1）對輪廓線以等弧長間隔進行重采樣N′個點c0，c1，…，cN′－1近似表達原始輪廓線，其中，N′＝2n，n是滿足2n＞N的最小整數，然后計算Lt（ci）。

（2）對每一個Lt（ci）進行快速傅里葉變換，其形式為

以｜zt（m）｜描述第t級弦長函數，｜zt（0）｜＝1，取N′個系數中的前M 個，構造向量μt＝［｜zt（1）｜｜zt（2）｜…｜zt（M）｜］代替第t級弦長函數描述形狀，得到有序集μ＝［μ1μ2…μK／2］Τ。以相同方法對S（ci）進行傅里葉變換，得到系數向量s＝［｜S（1）｜｜S（2）｜…｜S（M）｜］，于是通過μ和s描述整個形狀。因此，即使兩輪廓線上的點數不一致，但因為對所有弦長和中心距離進行傅里葉變換，在度量相似性時，兩個形狀都取變換系數中的前M個進行比較，故可以解決點數不一致的問題，同時，μ和s獨立于輪廓線的起始點（證明略）。

至此，得到滿足旋轉、平移、縮放不變性，且滿足緊致性和獨立于輪廓線起始點的形狀描述子μ和s。故可以用μ和s度量兩個形狀之間的形狀相似度：設形狀A和形狀B的μ、s分別為μA＝和A和B之間的形狀差異度定義為

｜sA－sB｜、｜μAi－μBi｜均指向量之間的歐氏距離，權系數w1、w2之和為1，μ、s均做了歸一化處理，故d（A，B）shape∈［0，1］，則形狀相似度sim（A，B）shape＝1－d（A，B）shape，且sim（A，B）shape∈［0，1］。因為中心距離函數可以刻畫整體形狀特征［8］，故當K值較小時，ds和dμ均可度量兩形狀的整體差異性，當K值較大時，dμ可度量細節差異性。

3.2 面向兩類應用的幾何相似度量模型建立

無論是第一類還是第二類模型，都要度量兩目標對應形狀的幾何相似性。因此，可以將這兩類模型統一于一個模型，僅在應用的過程中調節相關參數即可。設待度量的兩目標為A和B，度量其幾何相似性的總體思路與文獻［4］基本一致，都是從兩目標空間位置的鄰近程度、形狀、方向和大小（或長度）相似性程度綜合考慮并加權求和，但文獻［4］未考慮方向相似程度，且本文提出計算空間位置鄰近程度及形狀相似性程度均與文獻［4］不同。設［a1a2a3a4］Τ、［b1b2b3b4］Τ分別為描述A和B的向量，各分量代表位置、方向、大小（或長度）和形狀分量。d（A，B）表示A和B的差異度，sim（A，B）表示A和B的相似度，則A、B的幾何相似性可通過下式來計算

采用加權的Minkowski距離來度量d（A，B），則式（3）轉化為

式中，p值取2；ωj為權系數，且bj｜（j＝1，2，3，4）是經過歸一化后的值，其含義是A和B中第j個分量的差異度，故｜aj－bj｜∈［0，1］，d（A，B）∈［0，1］，sim（A，B）∈［0，1］。

對空間位置的鄰近程度度量，文獻［4］提出的方法僅能度量面目標，不能度量線目標。對此，利用Hausdorff距離來度量線目標或面目標之間的鄰近距離。但傳統Hausdorff距離易受目標局部變形程度影響，為此，基于高斯概率統計模型改進Hausdorff距離。基本思路是：先計算A上的每個點與B上所有點的最小距離集合Df（A，B）；然后計算B上的每個點與A上所有點的最小距離集合Db（B，A），最后根據拉依達3σ準則，剔除局部變形較大點，具體步驟為：

（1）計算Df（A，B）和Db（B，A）及其均值和均方差

（2）對Df（A，B）中的任意元素dft，t＝1，2，…，m，m為A上的點數，如果它滿足不等式

則認為此元素為A的內點，放入D′f（A，B）中，否則舍棄；對Db（B，A）存在類似操作，形成D′b（B，A）。

（3）令dfmax＝max｛D′f（A，B）｝，dbmax＝max｛D′b（B，A）｝，則A和B的Hausdorff距離為

設Hkmax（A，B）為A和B點集中兩點最大距離，則第一個分量｜a1－b1｜＝Hk（A，B）／Hkmax（A，B）是經過歸一化處理后的Hausdorff距離值。

空間目標的方向以MABR（minimum area bounding rectangle）的長軸方向角代替，故第二個分量方向差異度為｜a2－b2｜＝｜θA－θB｜／π，θA、θB分別為A、B的方向角；第三個分量面積或周長差異度為｜a3－b3｜＝｜SA－SB｜／max（SA，SB），SA、SB分別為A、B的面積或周長；第四個分量形狀差異分量采用3.1節式（2）的計算方法計算，即｜a4－b4｜＝dshape（A，B）。將上述四個分量帶入式（4）即可得到目標A、B的總的幾何相似度。

利用上述幾何相似度量模型進行空間目標匹配的基本步驟是：設A為待匹配的目標，利用式（4）逐一度量A與指定數據集D中的所有目標的幾何相似度，然后從D中找到一個與A最相似的目標C，且當sim（A，C）的值大于給定的閾值sim0時，認為A與C匹配，否則不匹配。為提高匹配效率，可以縮小D的范圍，方法是在A的最小外接矩形的橫向和縱向加一個兩數據集幾何位置偏移最大Hausdorff距離maxDist，然后形成擴展的最小外接矩形EMBR（enlarge minimum bounding rectangle），處于EMBR內的目標集合構成集合D。

利用幾何相似度量模型度量同一目標在化簡前后變形程度的基本思路是：設A為原始目標，以不同的化簡閾值對A進行化簡后得到的新目標序列為B1，B2，…，Bn，然后利用式（4）分別計算sim（A，Bi）（i＝1，2，..，n）的值，進而探尋不同化簡算法對形狀保持程度的規律。

3.3 相關參數及閾值的確定

匹配過程中的相關參數及閾值的確定：

（1）M和K的確定。因傅里葉變換的高頻易受噪聲影響，故M不能太高，根據文獻［9］，M暫取為10，根據經驗，K值暫取為8。后文還會對M，K的取值進行討論。

（2）其余參數的確定。引入相關反饋技術來確定匹配過程中的各種閾值［12］，匹配前，先選取一定數量的正例樣本（已經確定匹配的目標），分別計算ds、dμ、｜aj－bj｜（j＝1，2，3，4）的值，并求上述每個分量的標準差，取倒數并歸一化，分別得到式（2）和式（4）中的權值w1、w2和ωj（j＝1，2，3，4），最后根據式（4）計算每對正例樣本的相似值，并計算其均值標準差σ，則

圖形化簡前后相似度計算過程中相關參數及閾值的確定：M的值與匹配過程一致，由于對形狀的細節特征更要顧及，因此K值要更大。ωj、w1和w2的取值可根據對目標變形的關注程度調整。

4 實例及分析

4.1 多尺度幾何匹配試驗

匹配對應兩種數據源分別為：現勢性截止于2005年的4幅1∶25萬數據，現勢性截止于2009年的1幅1∶50萬數據。經坐標系統一后將兩種數據源疊加在一起，以1∶50萬水域要素匹配1∶25萬水域要素。

4.1.1 面狀水庫及島嶼的匹配

經統計，1∶25萬數據中共有面狀水庫102個，島嶼78個，1∶50萬數據中共有面狀水庫67個，島嶼49個。匹配的基本過程是：

（1）選取10對正例樣本，就可計算出ds、dμ、｜aj－bj｜，如表1所示。

表1 樣本相似特征分量及總相似值Tab.1 The swatch similarity characteristic components and general similarity value

得到ds和dμ對應標準差分別為0.017 5和0.069 1，則w1和w2的值分別為0.797 7和0.202 3。得到｜aj－bj｜（j＝1，2，3，4）的標準差分別為0.024 8、0.013 1、0.071 5、0.022 9，則ωj的值分別為0.231 4、0.437 3、0.080 2、0.251 0。得到sim的標準差為0.022 7，均值為0.950 4，則sim0的值為0.882 3。

（2）將上述閾值代入式（4），然后根據3.2節匹配面狀水庫和島嶼。記n1為匹配結果集中所有實體對的數目；r為n1中正確的匹配數目；n2為兩種數據源中同名實體的對數。定義查準率P＝r／n1，查全率R＝r／n2。本例中，水庫漏匹配8個，故n1＝67－8＋49＝108，在n1中沒有誤匹配，故r＝108，查看相似值小于sim0的實體集，發現漏匹配的8個水庫中，有3個在1∶25萬數據中為常年湖，另外3個是因為形狀差異太大（圖4（c）），2個是因為在1∶25萬數據沒有相應的實體。故n2＝67－3＋49＝111，則P＝100%，R＝97.4%。圖4是從結果集中選取的島嶼匹配的正例1個（圖4（a）），水庫匹配的正例1個（圖4（b）），水庫漏匹配的負例1個（圖4（c）），實線包圍區域為1∶50萬數據，陰影部分為1∶25萬數據。

圖4 面目標的匹配Fig.4 Area matching

A1對應搜索對象集合包括B1和B2；A2對應搜索對象集合也包括B1和B2；A3僅包括B3；A4僅包括B4。表2是圖4的匹配結果。

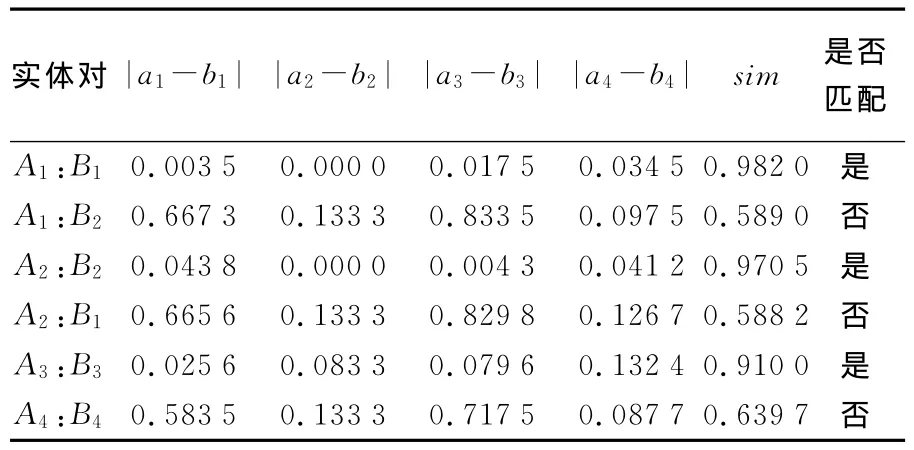
表2 圖4的匹配結果Tab.2 The results of Fig.4

4.1.2 線狀河流的匹配

選取10對已匹配樣本，得到w1和w2的值分別為0.660 2和0.339 8。ωj的值分別為0.302 5、0.219 4、0.191 0、0.287 1，sim0的值為0.882 4。圖5是兩種數據疊加在一起的顯示效果，實線為1∶50萬數據，虛線為1∶25萬數據，圖的左邊部分是局部放大圖。先根據河流代碼將1∶25萬數據進行合并，合并的方法是先進行節點匹配，然后逐段合并1∶25萬數據中河流代碼相同的目標，例如，B3是由P1P2和P2P3段合并而成。經統計，該區域共有1∶50萬河流58條，其匹配結果為：55條正確匹配，2條漏匹配，1條是因為1∶25萬數據無此目標，故P＝100%，R＝96.5%。從圖5中選取一個正例（左上圖）和負例（左下圖），A1對應搜索對象集合包括：B1、B2、B3和B4，A2僅包括B5，表3是具體的匹配結果。

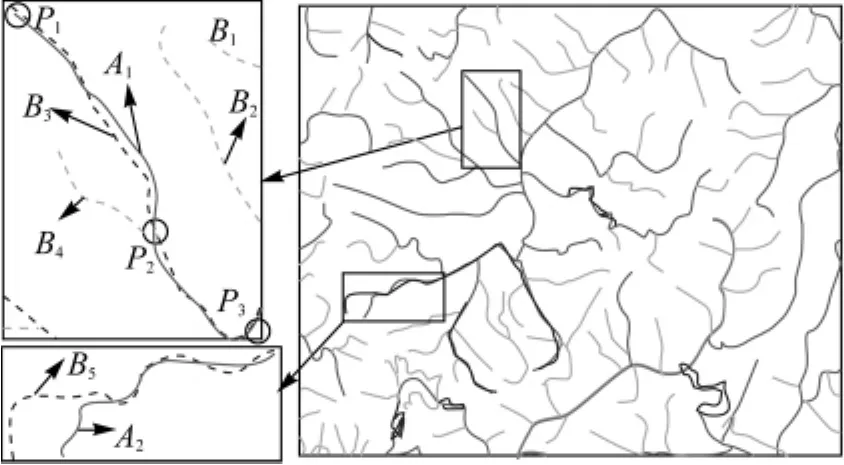
圖5 線目標的匹配Fig.5 Line matching

表3 圖5的匹配結果Tab.3 The results of Fig.5

4.1.3 算法比較

比較本文與文獻［2］所提出的利用緩沖區增長方法而不用幾何相似性度量方法在匹配的查準率、查全率和效率上的不同，同時與文獻［4］所提出的形狀相似度量方法進行比較。所利用的數據與前文所述一致，分別比較線目標和面目標匹配結果，具體結果如表4所示。通過分析，文獻［2］與本文相比，查準率一樣，即沒有錯誤匹配出現，但查全率降低，即出現漏匹配。漏匹配的原因是當兩線目標空間位置相鄰較遠時，文獻［2］提出的方法不能匹配這兩目標，而利用本文方法，即使兩線目標距離較遠，只要總體形狀具有很大的相似性，仍然可以匹配。從匹配速度上看，文獻［2］的方法較低，因為要構建線目標緩沖區，所以耗時較長；文獻［4］與本文相比，查準率仍然一樣，查全率也降低，原因是文獻［4］提出的形狀相似度量方法適用于同比例尺目標的匹配，當度量不同比例尺上的同一目標時，相似值差別會很大，因此可能導致漏匹配，如圖4（b）所示情況，匹配速度與本文基本相同。

表4 匹配算法的比較Tab.4 The comparison of matching algorithms

4.1.4 K和M值對匹配結果的影響分析

仍以上述數據為試驗數據，比較當K分別取2、4、8、16和32和M取1～20時查準率P和查全率R的變化情況，如圖6所示。

圖6 K和M值對匹配性能的影響Fig.6 The matching results for different Kand M

由圖6可知，當K＝8時，無論對面目標或線目標的查全率和查準率，都能達到最大。當M取 9、10、11、12時線目標匹配查準率和查全率能達到最大。

4.2 圖形化簡前后的相似性度量

以1∶25萬水域要素為原始數據，利用Douglas－Peucker（簡稱D－P）和Li－Openshaw（簡稱L－O）對目標以不同的閾值化簡，然后利用式（4）度量化簡前后的相似值，探尋相似值隨化簡閾值的變化情況。取參數M＝10，K＝16，w1＝w2＝0.5，ωj的值為0.25，表示對化簡前后目標在空間位置、方向、大小和形狀上變化的關注程度一致。D－P和L－O方法對應化簡閾值d的初始值為0.05mm，步長也為0.05mm，最大值為1mm，對圖7所示實心水庫進行化簡，分別得到20個化簡結果和相似值。圖7是化簡閾值分別為0.55mm和1mm時兩種化簡方法對應的結果。

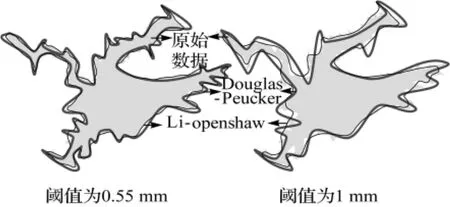
圖7 兩種化簡方法的對比Fig.7 The comparison of two methods of simplification

圖8（a）是總相似值sim（A，Bi）隨d而變化的曲線，圖8（b）是形狀總相似值1－｜a4－b4｜隨d而變化的曲線，根據3.1節，1－ds即為整體形狀相似值，圖8（c）是1－ds隨d而變化的曲線。當K＝16時，本文提出的形狀多級描述方法可以度量局部相似值，1－dμ是局部形狀相似值，圖8（d）是1－dμ隨d而變化的曲線。分析圖8，可得出以下結論：

（1）當0＜d≤0.55時，D－P和L－O對應總相似值具有基本相同的變化規律，用最小二乘線性擬合該區間的相似值得到sim（A，Bi）D－P＝－0.088 1d＋0.997 4，sim（A，Bi）L－O＝－0.070 3d＋0.991 3；當0.55＜d≤1時，D－P對應總相似值sim（A，Bi）隨d而變化的變化率要明顯比L－O大，用最小二乘線性擬合該區間的相似值得到sim（A，Bi）D－P＝－0.060 8d＋0.982 0，sim（A，Bi）L－O＝－0.003d＋0.959 8。

（2）與總相似值sim（A，Bi）的變化規律類似，形狀總相似值、整體形狀相似值和局部形狀相似值在0＜d≤0.55時，D－P和L－O具有基本相同的變化規律，但當0.55＜d≤1時，L－O對應形狀變化比D－P更具有穩定性。由此說明當化簡閾值在較小范圍變化時，D－P和L－O對形狀的保持基本一致，但當化簡閾值超出這一范圍時，D－P算法對化簡前后形狀的保持要比L－O算法差。

圖8 相似值隨化簡閾值變化的曲線Fig.8 The relationships between similarity value and simplification threshold

5 總 結

本文主要工作及創新點包括：

（1）組合多級弦長函數和中心距離函數描述空間數據幾何形狀，達到形狀描述的緊致性和唯一性，該方法的最大優點是通過調節K值可以從整體到詳細逐級描述形狀，滿足多尺度相似性度量要求和兩類相似性度量模型的應用需求；通過多級弦長和中心距離的離散傅里葉變換，解決兩形狀輪廓線點數不一致和起始點不一致的問題。

（2）基于形狀的多級描述方法建立顧及形狀、方向、長度和空間位置的第一類相似性度量模型，并將其應用于不同比例尺空間數據的幾何匹配，在此過程中，利用高斯概率統計模型改進傳統的Hausdorff距離，提高抗噪水平；引入信息檢索中相關反饋技術解決模型中閾值的確定問題。線目標和面目標的匹配試驗表明，該模型可有效實現不同比例尺之間水域要素的匹配。

（3）基于第一類相似性度量模型建立了第二類相似度量模型，然后比較兩類經典的化簡算法Douglas－Peucker算法和Li－Openshaw算法在化簡前后形狀相似值隨化簡閾值變化的規律。

［1］ DUEKHAM M，WORBOY F.An Algebraic Approach to Automated Information Fusion［J］.International Journal of Geographical Information Science，2005，19（5）：537－557.

［2］ ZHANG M，SHI W，MENG L Q.A Generic Matching Algorithm for Line Networks of Different Resolutions［C］∥Proceedings of the 8th ICA Workgroup on Generalization and Multiple Representations.LA Coruna：ICA，2005：1－8.

［3］ GOMBOSI M，ZALIK B，KRIVOGRAD S.Comparing Two Sets of Polygons［J］.International Journal of Geographical Information Science，2003，17（5）：431－443.

［4］ HAO Yanling，TANG Wenjing，ZHAO Yuxin，et al.Areal Feature Matching Algorithm Based on Spatial Similarity［J］.Acta Geodaetica et Cartographica Sinica，2008，37（4）：204－209.（郝燕玲，唐文靜，趙玉新，等.基于空間相似性的面實體匹配算法研究［J］.測繪學報，2008，37（4）：204－209.）

［5］ TONG Xiaohua，DENG Susu，SHI Wenzhong.A Probabilistic Theory－based Matching Method［J］.Acta Geodaetica et Cartographica Sinica，2007，36（2）：210－217.（童小華，鄧愫愫，史文中.基于概率的地圖實體匹配方法［J］.測繪學報，2007，36（2）：210－217.）

［6］ FU Z L，WU J H.Entity Matching in Vector Spatial Data［C］∥The International Archives of the Photogrammetry，Remote Sensing and Spatial Information Sciences.Beijing：ISPRS，2008：146－147.

［7］ BIAN Lihua，YAN Haowen，LIU Jiping，et al.An Approach to the Calculation of Similarity Degree of a Polygon before and after Simplification［J］.Science of Surveying and Mapping，2008，33（6）：207－208.（邊麗華，閆浩文，劉紀平，等.多邊形化簡前后相似度計算的一種方法［J］.測繪科學，2008，33（6）：207－208.）

［8］ TANG Luliang，LI Qingquan，YANG Bisheng.Shape Similarity Measuring for Multi－resolution Transmission of Spatial Datasets over the Internet［J］.Acta Geodaetica et Cartographica Sinica，2009，38（4）：336－340.（唐爐亮，李清泉，楊必勝.空間數據網絡多分辨率傳輸的幾何圖形相似性度量［J］.測繪學報，2009，38（4）：336－340.）

［9］ ZHANG D S，LU G J.Study and Evaluation of Different Fourier Methods for Image Retrieval［J］.Image and Vision Computing，2005，23（1）：33－49.

［10］ SEO C K，TAE J K.Texture Classification and Segmentation Using Wavelet Packet Frame and Gaussian Mixture Model［J］.Pattern Recognition，2007，40（4）：1207－1221.

［11］ CHEN Shi，MA Tianjun，HUANG Wanhong，et al.Gait Recognition Based on Shape Context Descriptor［J］.Pattern Recognition and Artificial Intelligence，2007，20（6）：794－799.（陳實，馬天駿，黃萬紅，等.基于形狀上下文描述子的步態識別［J］.模式識別與人工智能，2007，20（6）：794－799.）

［12］ WU Hong，LU Hanqing，MA Songde.A Survey of Relevance Feedback Techniques in Content－Based Image Retrieval［J］.Chinese Journal of Computers，2005，28（12）：1969－1979.（吳洪，盧漢清，馬頌德.基于內容圖像檢索中相關反饋技術的回顧［J］.計算機學報，2005，28（12）：1969－1979.）